Wat(t) is vermogen?
Watts hebben met vermogen te maken, watt-sekonden met energie en kilowatturen met onze portemonnee. Voor al diegenen die interesse hebben voor dat laatste aspekt staat elders in dit nummer een ontwerp van een watt-meter. Het rekensommetje is dan eenvoudig: gemeten watts maal bedrijfsuren is watt-uren; gedeeld door duizend is kWh; tenslotte de omrekeningsfaktor van de elektriciteitsleverancier toepassen en de guldens en centen zijn bekend. Toch heeft enig teoretisch inzicht ook z'n nut. Het verschil tussen "energie" en "vermogen", de betekenis van "effektieve waarde" en de reden waarom multimeters niet zonder meer geschikt zijn voor het meten van niet-sinusvormige spanningen; in dit artikel komen deze zaken aan de orde.
"Wanneer in een elektrische geleider met een weerstand R gedurende een tijd t een stroom I vloeit, komt in die geleider een hoeveelheid energie W in de vorm van warmte vrij die evenredig is met de tijd, met de grootte van de weerstand en met het kwadraat van de grootte van de stroom, in formule:
W = I2 × R ×t
Het was de Engelse fysicus J.P. Joule (1818 - 1889), bierbrouwer van beroep, waaraan we deze formulering te danken hebben. Gebruikmakend van de Wet van Ohm kunnen we ook schrijven:
W = U × I × t
Elektrische energie wordt uitgedrukt in de dimensie "watt-sekonde" of "joule". Bij het berekenen van ons elektriciteitsverbruik wordt meestal de eenheid kilowatt-uur (kWh) gehanteerd; de getallen blijven daardoor beperkt, voor de elektriciteitsrekening maakt het (helaas) niets uit (1 kWh = 3.600.000 watt-sekonde). Weliswaar is het woord "energieverbruik" in onze taal ingeburgerd, doch in feite kan energie niet verbruikt worden. Wel kan energie omgezet worden in een andere vorm (volgens Einstein zelfs in massa en omgekeerd); er gaat dus niets verloren. De mogelijkheid om een hoeveelheid energie in een bepaalde tijd om te zetten in een andere vorm, noemt men vermogen. Het vermogen P is dus gelijk aan de energie-(omzetting) W per eenheid van tijd:
P = W / t
oftewel:
P = U × I
Wanneer we te doen hebben met een gelijkspanning over een weerstand, is het berekenen van het vermogen een vrij eenvoudige zaak. Het is een kwestie van vermenigvuldigen van spanning en stroom. Aangezien in dit geval de spanning konstant is, geldt dat ook voor de stroom. Het vermogen zal dus op elk tijdstip gelijk zijn. In figuur 1 is dat in de vorm van grafieken duidelijk gemaakt. Op tijdstip to schakelen we de gelijkspanning in (figuur 1a), waardoor een stroom door de weerstand zal lopen (figuur 1b). Vermenigvuldigen we beide waarden, dan vinden we het vermogen (figuur 1c). Bij een spanning van bijvoorbeeld 24 V en een stroom van 2 A bedraagt het vermogen 48 watt. Aangezien zowel de spanning als de stroom konstant blijft, zal het vermogen op tijdstip ti gelijk zijn aan dat op tijdstip t0. Het in grafiek uitzetten van dit vermogen levert de in figuur lc getekende rechte lijn op. Indien we van een verbruiker eenmaal het vermogen berekend hebben, kunnen we de hoeveelheid verbruikte elektrische energie bepalen door het vermogen te vermenigvuldigen met de tijd die de verbruiker ingeschakeld is. In figuur 1c stelt het gearceerde oppervlak de elektrische energie voor die op tijdstip t1 na het inschakelen door de weerstand omgezet is in warmte. Dit oppervlak is het produkt van spanning, stroom en tijd; energie dus. Een kilowatt-uurmeter voor gelijkstroom zou dus samengesteld kunnen worden uit een voltmeter, een ampèremeter en een klok!
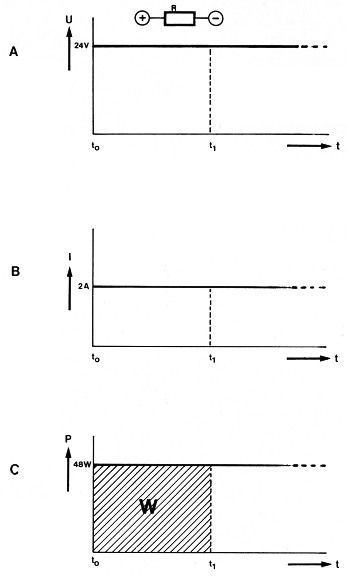
Figuur 1. Zoals al uit de benamingen blijkt, blijft de waarde van een gelijkspanning (a) en een gelijkstroom (b) gelijk. Het produkt van deze waarden levert een konstant blijvend vermogen op (c). Het gearceerde oppervlak is de hoeveelheid elektrische energie (vermogen × tijd) die in de tijd van to tot t1 in een weerstand omgezet is in warmte.
Het lichtnet echter levert geen gelijkspanning, en daardoor ook geen gelijkstroom, maar een nagenoeg sinusvormige wisselspanning met een frekwentie van 50Hz. Het zal duidelijk zijn dat wisselstroomvermogens niet berekend kunnen worden met formules die voor gelijkstroomvermogens gelden. De eerste moeilijkheid doet zich voor bij het uitdrukken van de in de tijd variërende waarde van de wisselspanning en -stroom. Nog vervelender wordt het wanneer de verbruiker zich niet als een ohmse weerstand gedraagt, vanwege zijn induktieve (spoel) op kapacitieve (kondensator) karakter. De wisselstroom is dan niet meer in fase met de wisselspanning; er ontstaan hierdoor momenten waarop er een positieve stroom loopt terwijl de spanning negatief is (waarover straks meer). Sommige verbruikers maken het nog bonter en nemen ondanks de sinusvormige netspanning toch geen sinusvormige stroom op. En dan zwijgen we nog maar even over gevallen waarbij slechts gedeelten van de netspanningsperioden aan de verbruiker worden toegevoerd (bij v. triacregelingen zoals toegepast in lichtdimmers), bij niet-ohmse belastingen ontstaan dan de meest vreemde stroomvormen.
Laten we met het eenvoudigste geval van wisselstroomvermogen beginnen. In figuur 2a is de in de tijd variërende spanning van het lichtnet getekend. De waarde van de spanning verloopt volgens een sinusfunktie. Sluiten we deze spanning aan op een konstant blijvende (lineaire), zuiver ohmse verbruiker (bije. een elektro-oven), dan zal een stroom ontstaan die eveneens volgens een sinusfunktie verloopt (figuur 2b). Vermenigvuldigen we de waarde van de netspanning en de -stroom op een bepaald tijdstip, dan is het vermogen op dat tijdstip (de momentele waarde) bekend. Door op die manier op diverse tijdstippen binnen de periode T het momentele vermogen te bepalen en de gevonden waarden in een grafiek uit te zetten, ontstaat de vermogenskromme uit figuur 2c. Om het in de tijd variërende vermogen in een waarde te kunnen uitdrukken, moet het gemiddelde vermogen over een periode bepaald worden (het gemiddelde vermogen over de andere perioden is gelijk). Dat is niet zo eenvoudig. Het uitmiddelen van het vermogen is in feite niets anders dan de hoeveelheid energie in een periode (gearceerde oppervlak in figuur 2c) te delen door de periodetijd T. Wanneer we de periode in oneindig veel kleine stukjes At verdelen, dan kunnen we stellen dat binnen zo'n kort tijdsbestek Ot zowel de spanning als de stroom konstant blijft. De hoeveelheid energie die in At geleverd wordt is dan volgens de gelijk-stroomberekening gelijk aan:
Δw = u × i × Δt
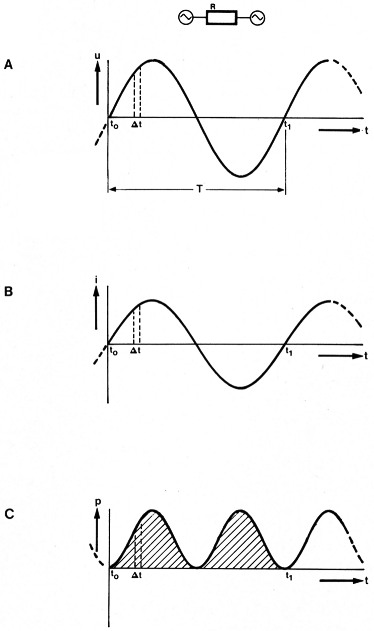
Figuur 2. Wanneer een sinusvormige spanning (a) op een weerstand aangesloten wordt, ontstaat er een eveneens sinusvormige stroom (b). Bepalen we op verschillende tijdstippen binnen de periode T het (momentele) vermogen en zetten we de gevonden resultaten uit in een grafiek, dan ontstaat de vermogenskromme uit figuur 2c. Via integraal-rekenen kan het gemiddelde vermogen precies berekend worden.
Alle stukjes Δw bij elkaar opgeteld, levert de totale elektrische energie op die in een periode aan de weerstand toegevoerd wordt. Delen we die hoeveelheid door de periode-tijd T, dan volgt daaruit het gemiddelde vermogen P. Dat uitrekenen van al die kleine oppervlakjes Aw levert een onbegonnen rekenwerk op. Via integraalrekenen gaat dat een stuk gemakkelijker (en nauwkeuriger). We besparen u die wiskundige bewerking. In veel praktijkgevallen is die ook niet nodig, zoals nu zal blijken. Om op een eenvoudigere wijze wissel-stroomvermogens te kunnen berekenen is het begrip "effektieve waarde" ingevoerd. De effektieve waarde van een variërende stroom is gelijk aan die van een gelijkstroom die in eenzelfde ohmse weerstand gedurende eenzelfde tijd een gelijke hoeveelheid warmte (= energie) opwekt. Met het begrip "effektieve waarde" vertalen we dus een wisselstroom in een gelijkstroom met hetzelfde effekt! Is de effektieve waarde van de stroom bekend, dan levert het kwadraat hiervan vermenigvuldigd met de weerstand het vermogen op:
P = Ieff2 × R
En evenzo geldt:
P = Ueff2 / R
Ook kunnen we het vermogen in een ohmse weerstand berekenen door de effektieve waarde van de stroom met die van de spanning te vermenigvuldigen:
P = Ieff × Ueff
De effektieve waarde van een stroom of een spanning moet ook weer via integraalrekenen bepaald worden. In zoverre is het voor de minder wiskundigen onder ons er niet eenvoudiger op geworden. Voor sinusvormige spanningen bestaat er echter een gemakkelijk te onthouden verband tussen de topwaarde û en de effektieve waarde:
Ueff = û / √2 ≈ 0,71 × û
De wisselspanning van het lichtnet bijvoorbeeld heeft een topwaarde van ca. 311 volt. De effektieve waarde is dus gelijk aan 311 V × 0,71 = ca. 220 volt.
Ook voor sinusvormige stromen geldt een dergelijk verband:
Ieff = î / √2 ≈ 0,71 × î
De meeste wisselstroom- en spanningsmeters (multimeters) zijn zo geijkt dat ze direkt de effektieve waarde van een sinusvormige (!) stroom of spanning aanwijzen; er hoeft dan niet meer gerekend te worden.
Zoals al eerder opgemerkt is, gedragen veel huishoudelijke apparaten zich niet als een ohmse weerstand, maar hebben een induktief of kapacitief karakter. Er treedt dan een faseverschil op tussen de spanning en de stroom; de stroom ijlt na of voor op de spanning. In figuur 3 is de situatie geschetst bij een induktieve belasting (die voorgesteld kan worden als een serieschakeling van een spoel en een weerstand). Het blijkt dat de stroomperioden in tijd verschoven zijn t.o.v. de spanningsperioden. In figuur 3c is de vermogenskurve uitgezet op gelijke wijze als dat in figuur 2c gebeurd is. In figuur 3c valt echter iets vreemds te ontdekken, namelijk de zwarte vlakjes "negatieve energie". Dat is energie die door de induktieve komponent aan het net terug-geleverd wordt (moet dus van het positieve verbruik afgetrokken worden) en dus niet aan het werkelijk energieverbruik deelneemt. De spoel neemt in feite een teveel aan stroom uit het net op om een magnetisch veld op te bouwen en levert dat even later bij het afbreken van het veld weer terug aan het net. Er is dus sprake van een hoeveelheid energie die niet nuttig gebruikt wordt. Men spreekt dan ook van blindvermogen of reaktief vermogen. Vermenigvuldigen we zonder meer de effektieve waarde van de stroom en de spanning, dan levert dat het zogenaamde schijnbaar vermogen Ps op (uitgedrukt in de eenheid volt-ampère VA):
Ps = Ueff × Ieff
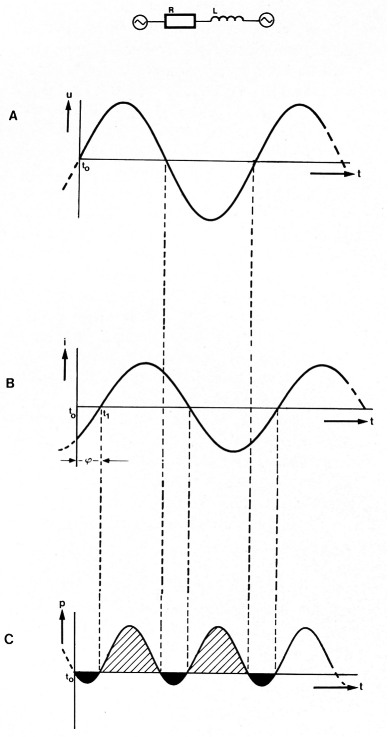
Figuur 3. Bij een induktieve verbruiker ijlt de stroom (b) na op de spanning (a). Daardoor ontstaan momenten dat de waarde van het vermogen negatief wordt (zwarte gedeelten in figuur 3c). De hoeveelheid energie die in een periode in de weerstand omgezet wordt in warmte, moet gezien worden als het verschil in oppervlakte van de gearceerde en de zwarte vlakken.
Van dat schijnbaar vermogen wordt slechts een deel werkelijk benut, namelijk het werkelijk of werkzaam vermogen. Wiskundig valt af te leiden dat dit gelijk is aan:
P = Ueff × Ieff × cosφ
Op sommige apparaten heeft de fabrikant de cos lp-waarde bij nominale belasting vermeld. Het berekenen van het (werkelijk) vermogen is dan eenvoudig.
Alleen voor de werkelijk benutte energie krijgen we van de stroomleverancier de rekening gepresenteerd. De bekende elektromechanische kilowatt-uurmeter is dan ook zo gekonstrueerd dat deze alleen op het werkelijke vermogen reageert en dit met de tijd vermenigvuldigt.
De cos φ-waarde van een verbruiker kan liggen tussen 0 en 1. Een cos φ-waarde van 0 betekent dat we te doen hebben met een zuiver induktieve of kapacitieve belasting. Het faseverschil (i) tussenspanning en stroom is dan precies 90° (cos 90° = 0). Bij een cos φ-waarde van 0 bedraagt het werkelijk vermogen dus Ueff × Ieff × 0 = nul. Er wordt dus geen energie verbruikt (onze kWh-meter staat stil), terwijl er toch een stroom loopt! De elektriciteitsleverancier vindt dat een minder prettige situatie, want hij zal die blindstroom of watt-loze stroom moeten leveren en draait zelf voor de verliezen in het distributienet op. Ook betekent deze blindstroom een nodeloze beperking van de reserves van de generator in de elektriciteitscentrale (i.v.m. magnetische verzadiging). Het is dan ook niet voor niets dat de leverancier eisen stelt aan de totale cos φ-waarde bij grootverbruikers. Naarmate het ohmse deel van de induktieve of kapacitieve belasting groter is, neemt de cos φ-waarde toe. Bij een zuiver ohmse belasting zijn stroom en spanning in fase: de cos φ-waarde bedraagt dan 1 (cos 0° = 1).
Bij gebruik van een triacregeling ontstaat een verre van sinusvormige spanning en stroom (zie figuur 4). De tot nu toe gebruikte formules voor het berekenen van de effektieve waarden gelden dan ook niet meer. Het gemiddelde vermogen is, wanneer de ontsteekhoek a bekend is, nog relatief eenvoudig te berekenen. Wanneer echter de stroom niet meer in een wiskundige notatie valt vast te leggen, kunnen we het berekenen wel helemaal vergeten. In de praktijk is dat maar al te vaak het geval. Een kollektormotor bijvoorbeeld (in koffiemolens, stofzuigers en boormachines) veroorzaakt een zo vreemde stroomkurve dat we alleen nog maar het vermogen kunnen meten. Een meter waarmee onafhankelijk van de aard van de belasting het vermogen (aantal watts) gemeten kan worden, zal dus geschikt moeten zijn voor de meest kurieuze spannings- en stroomvormen. In principe zal zo'n meter kontinu bezig moeten zijn met het bepalen van het momentele vermogen uit het produkt van de momentele spanning en stroom en het uitmiddelen hiervan. In de elektromechanische wattmeter (zie figuur 5) wordt het "momentele produkt" van stroom en spanning bepaald door een elektrodynamisch meetsysteem, bestaande uit twee spoelen: een hoogohmige spanningsspoel (Lu+R) en een laagohmige stroomspoel (Li). De robuustere stroomspoel is vast opgesteld en binnen deze spoel bevindt zich de draaibare spanningsspoel met daaraan vast de meternaald. De spanningsspoel wordt parallel en de stroomspoel in serie met de verbruiker X geschakeld. Ten gevolge van het magnetisch veld van de vast opgestelde stroomspoel, ondervindt de draaibare spanningsspoel via haar magnetisch veld een moment ("kracht") dat evenredig is met het produkt van de momentele spanning en stroom (= momenteel vermogen). Het meetsysteem is zodanig traag en gedempt dat snelle variaties in het moment uitgemiddeld worden, waardoor de naald keurig stil blijft staan en het (gemiddelde) vermogen aanwijst.
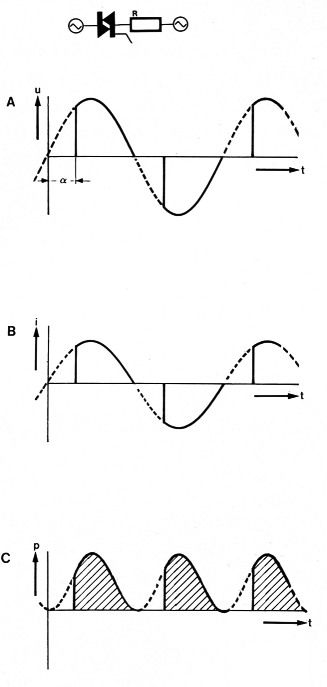
Figuur 4. Bij gebruik van een triacregeling worden, afhankelijk van de ontsteekhoek α, gedeelten van de spanningsperioden geblokkeerd (a). Er ontstaat dan geen sinusvormige stroom (b). Het berekenen van het gemiddelde vermogen (c) is dan ook minder eenvoudig.
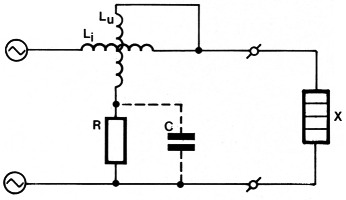
Figuur 5. Het elektrisch schema van een elektrodynamische watt-meter. Binnen een vast opgestelde stroomspoel (Li) bevindt zich een draaibare spanningsspoel Lu+R), waarop een wijzer is gemonteerd. De uitslag van de meter is evenredig met het gemiddelde produkt van stroom en spanning.
Voor een juiste aanwijzing moet de stroom door de spanningsspoel in fase zijn met de spanning over de verbruiker. Dat wordt bereikt door de spanningsspoel zuiver ohms te maken door het induktieve gedeelte kapacitief te kompenseren (in figuur 5 aangegeven met een gestippeld getekende kondensator C). Helaas geldt die kompensatie alleen maar voor een frekwentie. De vaak vreemde stroomvormen die verbruikers veroorzaken, bevatten echter een groot aandeel aan hogere harmonischen (veelvouden van de 50 Hz-frekwentie), waardoor de kompensatie niet meer klopt. Voor "kromme" spannings- en/of stroomvormen is de elektromechanische watt-meter dan ook minder nauwkeurig.
Het kan echter ook met een meetsysteem zonder spoelen: elektronisch. Elders in dit nummer treft u tekst en uitleg aan over de werking van zo'n elektronische watt-meter en hoe u die zelf kunt bouwen. Daarmee kunt u het vermogen meten van alle elektrische apparaten die u in huis hebt. En met een uitbreiding valt er ook nog een kilowatt-uurmeter (energie-meter) van te maken; handig wanneer u nu wel eens precies wilt weten hoeveel die koelkast aan "stroom" verbruikt.