Kristal-oven
Kwartskristallen zijn de korpponenten bij uitstek om een stabiele frekwentie op te wekken. Worden er echter aan de frekwentiestabiliteit hoge eisen gesteld, bijv. voor meetapparatuur, dan zal er nog wat meer nodig zijn dan louter en alleen een kristal en een oscillatorschakeling. De voornaamste "boosdoener" is toch wel de omgevingstemperatuur, van nature een nogal variabele faktor. Wanneer we de temperatuur van het kristal konstant weten te houden, zal de toch al stabiele frekwentie nog minder verlopen. In de oven dus!
Kristal-oscillatoren worden geacht een zeer nauwkeurige en stabiele frekwentie af te leveren. Op basis van hun piëzoelektrische eigenschappen bezitten kwarts-kristallen een zeer hoge kwaliteitsfaktor; veel hoger dan bijvoorbeeld een LC-kring. Wanneer er dus ergens een referentie nodig is, bijvoorbeeld in een ontvanger of in de tijdbasis van een frekwentiemeter of klok, dan grijpen we in eerste instantie naar een kristal-oscillator. Toch kan ook een kristalfrekwentie nog verlopen. Dit is te wijten aan verouderingseffekten, invloeden van de voedingsspanning en de belasting van de oscillatorschakeling, maar !nog het meest aan de temperatuurinvloed. Kijk maar eens naar figuur 1. Hier is voor een bepaalde kristalsnede (AT) de relatieve frekwentieafwijking ten opzichte van de slijpfrekwentie (in parts per million) als funktie van de temperatuur te zien. Goede kristallen hebben een kurve die over een groot temperatuurgebied zo vlak mogelijk verloopt. Voor een stabiele frekwentie mag de kristaltemperatuur in elk geval niet al te veel variëren. De omgevingstemperatuur van de oscillatorschakeling is echter wel aan veranderingen onderhevig (klimaat, opwarmen). Om deze invloeden te elimineren, wordt het kristal geplaatst in een met een thermostaat geregelde oven die het kristal op een konstante temperatuur houdt.
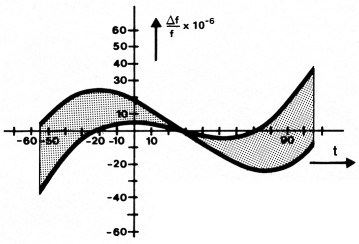
Figuur 1. De frekwentieafwijking van een kristal als funktie van de temperatuur (derdemachtskromme).
De ovenregeling
Het is de bedoeling om de kristaltemperatuur op een konstante waarde te houden. Dat kunnen we op de volgende manier doen: Het kristal wordt bevestigd op een metalen blokje dat door een verwarmingselementje opgewarmd wordt. Tevens komt er op het blokje een temperatuurvoeler die de temperatuur van het blokje meet. De meetwaarde wordt vergeleken met een referentiewaarde en aan de hand daarvan wordt het stookelement bijgeregeld. In figuur 2 zien we het blokschema van deze regeling.
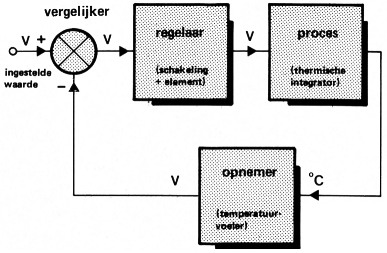
Figuur 2. Het blokschema van de oven-thermostaat.
Het regelen van dit proces lijkt eenvoudig, maar de inhoud van het blok "PROCES" gooit roet in het spreekwoordelijke eten. Er is namelijk een vertraging aanwezig tussen het opwarmen van het blokje en het meten van de temperatuur. Wanneer de sensor tijdens het opwarmen de ingestelde waarde meet, wordt door de regelaar het verwarmingselement omlaag-geregeld. Door de hoeveelheid warmte die in het metalen blokje aanwezig is, blijft de temperatuur nog even stijgen, ondanks het feit, dat het verwarmingselement niet meer stookt (te vergelijken met een centrale-verwarmingsregeling). Het resultaat van een door de regelaar uitgevoerde wijziging is pas na enige tijd merkbaar, zodat de ingreep in feite steeds te laat komt. Men zou natuurlijk deze dode tijd kunnen verkleinen door de massa van het blokje te verminderen, maar dat is ook weer niet de bedoeling. Deze massa heeft namelijk een soort "vliegwieleffekt" voor de temperatuur. Kleine kortstondige veranderingen van buitenaf beïnvloeden de temperatuur van het blokje nauwelijks.
In de regeltechniek bestaat er gelukkig een afdoende oplossing voor dit probleem, nl. de PI-regelaar. PI staat voor "proportioneel integrerend"; dit betekent dat het blok "regelaar" een bepaalde versterking heeft en tegelijkertijd integreert, dus een zeer hoge versterking voor DC. Er bestaan instelregels voor dit soort regelsystemen. Een hiervan is bijvoorbeeld dat de integratie-tijdkonstante voor een bepaalde sprongresponsie 3,3 maal de vertragingstijd in het proces behoort te zijn, terwijl de versterkingsfaktor niet zo groot mag zijn dat de regeling instabiel wordt.
De schakeling
In figuur 3a zien we de realisatie van het regelsysteem. De temperatuuropnemer is D1, een LM335. Deze levert een spanning van 10 mV/K. Op de niet-inverterende ingang van IC1 staat een spanning van 3,33 V, zodat het systeem regelt naar een sensortemperatuur van 333 K, dat is 60 °C. IC1 versterkt bijna oneindig voor DC (zodat de statische afwijking zeer klein is) en zdn 300× voor hogere frekwenties. De uitgang van IC1 stuurt T1, een (variabele) stroombron, gebruikt als verwarmingselement. De maximale stroom door deze transistor wordt door D2 begrensd op ca. 200 mA; dit om de regeling een beetje in toom te houden.
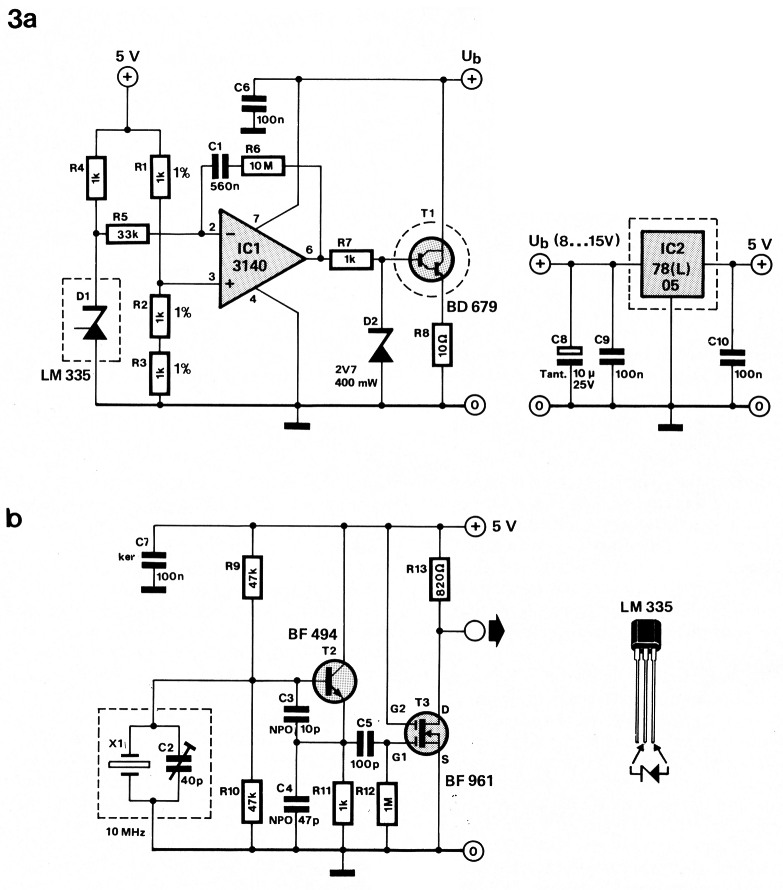
Figuur 3. Het totaalschema is opgedeeld in een "stook"deel (a) en een oscillatordeel (b).
Het is de bedoeling dat D1, T1 en IC2 op het metalen plaatje worden bevestigd, evenals het kristal en de trimmer (figuur 3b). Bij deze oscillator werkt het kristal in de parallelmode (het kristal heeft dan een hoge impedantie) met C2 voor fijn-afstelling van de frekwentie. Wanneer de gewenste frekwentie niet gehaald mocht worden, dan kan de trimmer eventueel ook in serie met het kristal worden geschakeld. We hebben hier een kristal genomen, dat geslepen is voor de nominale frekwentie bij kamertemperatuur. Wanneer men een echt ovenkristal (voor 60°) kan bemachtigen, zal men misschien het andere alternatief (trimmer in serie met het kristal) moeten nemen. C3 en C4 spelen niet alleen een rol in het oscillator-gedeelte, maar ze zorgen tevens voor een bepaalde kapacitieve afsluiting van het kristal (de houderkapaciteit). Het is zeer belangrijk, dat hiervoor types worden genomen met een temperatuurcoëfficient nul (NPO), te herkennen aan een zwarte markering. T3 zorgt voor een buffering tussen oscillatorsignaal en uitgang.
Bouw, afregeling en gebruik
De komplete schakeling wordt opgebouwd op een stukje gaatjesprint. Vooral de mechanische konstruktie rondom het metalen plaatje verdient wat meer aandacht. Hiervoor wordt een aluminium plaatje genomen van 3 mm dik en met de afmetingen van ca. 3 × 1,5 cm. Aan de ene zijde komen de transistor, het kristal en de trimmer te zitten, terwijl aan de andere zijde de spanningsregelaar en de LM335 bevestigd worden. In figuur 4 zien we een duidelijke tekening van het geheel. Het aluminium plaatje dient tevens als massa voor X1, C2, D1 en IC2. De verschillende massa-aansluitingen behoren ook daadwerkelijk met het plaatje verbonden te worden (bije via een boutje of een soldeerlipje). Het warmtetransport is dan optimaal. Ook het huisje van het kristal behoort plat op het plaatje gemonteerd te worden. Voor T1 gebruiken we een isolatieplaatje en warmtegeleidende pasta (deze pasta wordt ook gebruikt voor D1 en IC2). De instelling van de regelaar (R6/R5 en C1) hangt nauw samen met de mechanische konstruktie. Het is dan ook aan te bevelen om zoveel mogelijk het in figuur 4 geschetste voorbeeld aan te houden.
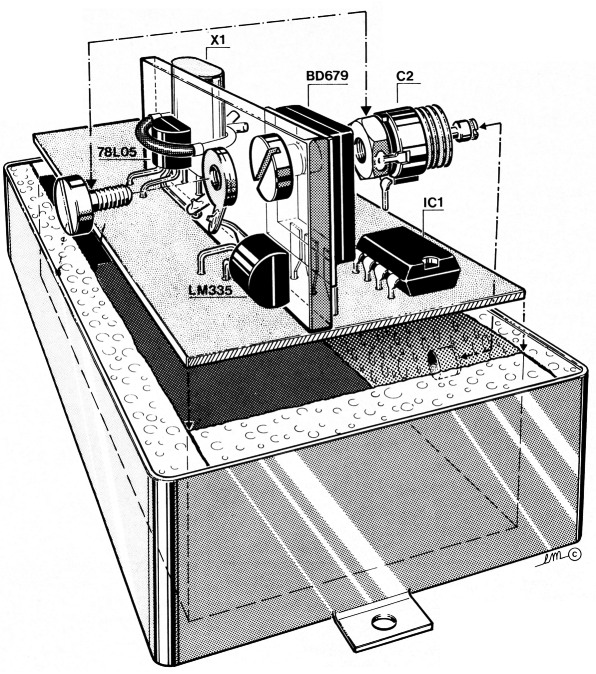
Figuur 4. Het konstruktieve aspekt van de oven: het plaatje dat op een konstante temperatuur gehouden moet worden.
Het bouwsel komt uiteindelijk in een metalen bakje te zitten dat aan de binnenzijde bekleed is met piepschuim, i.v.m temperatuurbeïnvloeding van buiten af. Het printje wordt hierin vastgeklemd of gelijmd. Verder behoren er nog twee gaatjes in het doosje te worden aangebracht: een voor de verbindingsdraadjes en een voor de instelling van de trimmer. De kwarts-oven kan heel goed dienen als nieuwe referentie voor de in januari '85 gepubliceerde µP-gestuurde frekwentiemeter. De uitgang van de schakeling wordt verbonden met de 10-MHz-ingang en de UB draad komt aan de U˜-aansluiting te liggen. Vanzelfsprekend worden ook de massa's doorverbonden. Vervolgens moeten we het regelgedrag van de schakeling kontroleren. Hiertoe schakelen we een draaispoel-voltmeter aan op de uitgang van IC1 en kontroleren, of de spanning zich na inschakelen stabiliseert op ca. 1,5...2 V (dit kan enkele minuten duren).
Dan de afregeling van de frekwentie. Dat de frekwentiestabiliteit voldoende is, weten we. Voor het proefmodel konden we in ieder geval "beter dan 1 ppm" noteren! Alleen moet er nog een nauwkeurige referentie gevonden worden, opdat de frekwentie exact op 10 000 000 Hz kan worden afgeregeld. Dat is een moeilijk geval. Voor afregel-gegadigden met een grote dosis geduld bestaat de volgende oplossing: Deel het 10-MHz-signaal naar een frekwentie van 50 Hz. Als we hierop een digitaal klokje laten lopen, kan aan de hand van de tijdseinen op de radio de frekwentie worden gechecked.
Is de afwijking na 24 uur 1 s, dan bedraagt de afwijking nog altijd 12 ppm! Het kan dus wel even duren, voordat de oscillator goed is afgeregeld! Degenen die Droitwich op 200 kHz goed kunnen ontvangen, kunnen proberen een meet-ontvangertje in elkaar te knutselen, dat aan de uitgang alleen de draaggolf afgeeft en de 90°-komponent van de draaggolf. Op een XY-skoop geeft dit een cirkel. Nu bieden we aan de Zingang (intensiteitsmodulatie) een 1-MHz-puls aan, afkomstig van de kristal-oven, met daarop aangesloten een 10-deler. Op het scherm ontstaat dan bij korrekte afregeling een cirkel of een ellips met vijf stilstaande onderbrekingen.