Temperatuur meten met ntc's

Krom wordt recht

NTC's zijn veel gebruikte temperatuursensoren, die in vele uitvoeringen en nominale waarden te verkrijgen zijn. Het niet lineaire verloop van de weerstand/temperatuur-kurve vereist echter een aangepaste versterker, bij een analoge toepassing, of bij digitale verwerking wat extra rekenwerk Beide methoden, die ook bij andere niet-lineaire sensoren kunnen worden toegepast, komen in dit artikel aan bod.

Voordat we echter aan het "rechttrekken" van de weerstand/temperatuurkurve kunnen denken, zal er eerst een bepaald type NTC - een weerstand met een sterk negatieve temperatuur-koëfficiënt (3 tot 6%/K) - moeten worden uitgezocht, zodat de bijbehorende kurve bekend is.

Fig 1
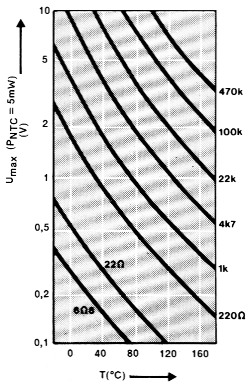
Figuur 1. In deze grafieken is te zien dat de spanning bij een toename van de temperatuur moet afnemen om het in de NTC gedissipeerde vermogen konstant te houden.

Keuze van een NTC

Bij de keuze van een bepaald type gaat men bijna altijd uit van de bouwwijze van de NTC, want die moet zijn aangepast aan het doel waarvoor de NTC wordt gebruikt. Er zijn speciale NTC's voor metingen in vloeistoffen, lucht, andere gassen en voor montage in of op massieve voorwerpen. Er zijn ook "kale" NTCelementen (tabletten) verkrijgbaar, die door de gebruiker voor een speciale toepassing kunnen worden afgewerkt.

Heeft men de keus laten vallen op een bepaald model, dan moet de nominale weerstand nog bepaald worden (worden opgezocht in het data-boek). De nominale weerstand is de weerstandswaarde bij een bepaalde temperatuur; meestal is dit 25 °C, maar het kan ook -30 of +100 °C zijn.

Fig 2
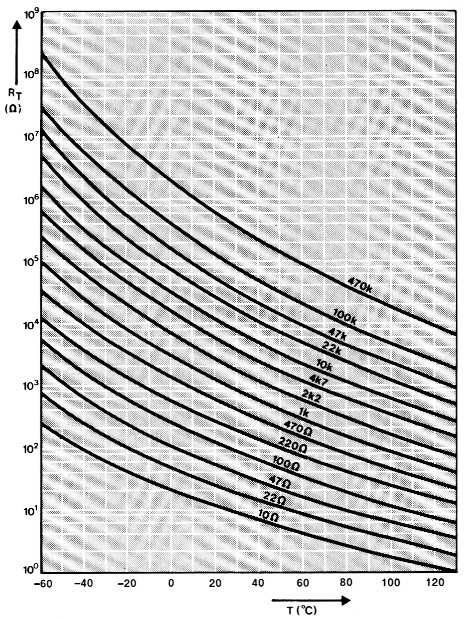
Figuur 2. De weerstand van de NTC als funktie van de temperatuur.

Via de weerstand van de NTC kunnen we de temperatuur meten. Ook de weerstand van de NTC wordt weer via een omweg gemeten. Deze omweg is bijna altijd de spanning over de NTC. Om nu het effekt van de temperatuur op de spanning over de NTC zo groot mogelijk te maken gaat de voorkeur uit naar hoogohmige typen. Het meetsignaal wordt namelijk groter naarmate de weerstand van de NTC, de voedingsspanning en de belastbaarheid van de NTC groter worden. De NTC mag echter niet te sterk worden belast, want het in de NTC gedissipeerde vermogen laat de temperatuur van de NTC stijgen en beinvloedt dus de meting. Daarom wordt van de NTC ook de warmtegeleiding (G_th in mW/K) opgegeven. Deze waarde geeft aan bij welke belasting de NTC-temperatuur 1 K (1 °C) warmer wordt. Bedenk daarbij dat voor een konstante belasting de spanning moet afnemen naarmate de temperatuur stijgt (de weerstand kleiner wordt). Als we dat met een grafiek zichtbaar maken, dan krijgen we een grafiek zoals die in figuur 1 is getekend voor de verschillende nominale waarden van een NTC van het type K164 bij een belasting van 5 mW. Goed te zien is, dat de hoogohmige typen veel meer spanning "verdragen" - en als gevolg daarvan meer meetsignaal kunnen afgeven - en dat de spanningsvariatie relatief klein is.

Linearisering van de R/Tkurve.

NTC's hebben een sterk niet-lineaire weerstand/temperatuurkarakteristiek. In figuur 2 zijn er enkele getekend. Vindt u het meevallen? Dan moet u nog eens goed naar de weerstand-schaal kijken, die is namelijk logaritmisch! Dat is ook te zien aan de formule waarmee deze kurven zijn te benaderen:

R_T = R_N × e^{B(1/T - 1/T_N)}

is:
R_T de weerstand bij temperatuur T,
R_N de weerstand bij temperatuur
T_N (de nominale weerstand),
B een konstante (wordt opgegeven in het databoek,
T de temperatuur (in kelvin).

Nu zullen we meestal voor een temperatuurmeting een lineaire schaal wensen. Met behulp van een serie- en een parallelweerstand is een goede lineariteit te bereiken. Afhankelijk van de eisen die aan de lineariteit wordt gesteld, mag het temperatuurbereik niet groter zijn dan 50 à 100 K.

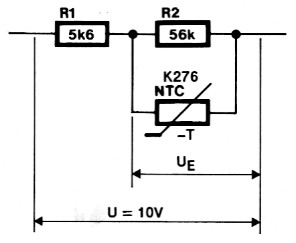
Een behoorlijke lineariteit verkrijgt men door de se- rieweerstand (R1 van figuur 3a) een waarde te geven die overeenkomt met de weerstand van de NTC in het midden van het gewenste temperatuurbereik en de parallelweerstand (R2) een waarde te geven die tienmaal zo groot is. In figuur 3b is het verloop van de signaalspanning UE van deze kombinatie getekend. Ook getekend is het vermogen dat in de NTC wordt gedissipeerd. De variatie van dit vermogen is relatief klein, zodat ook de verwarming ten gevolge hiervan min of meer konstant blijft - iets dat de nauwkeurigheid van de meting ten goede komt. Een nadeel van deze schakeling is, dat de gevoeligheid afneemt en het netwerkje niet belast mag worden, maar daar is met een (opamp-)versterker op eenvoudige wijze wat aan te doen.

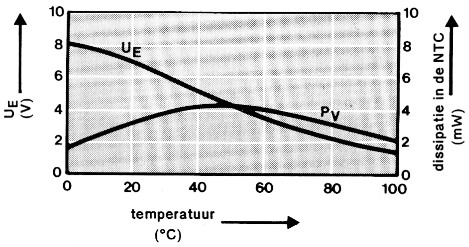
Fig 3a Fig 3b
Figuur 3. Een gelineariseerde NTC. De grafieken geven de spanning over en het gedissipeerde vermogen in de NTC weer.

Fig 4
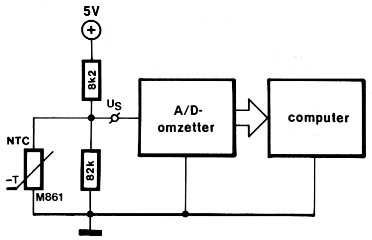
Figuur 4. Het principe van gecomputeriseerd temperatuur meten met een NTC.

De digitale benadering

Als de gemeten temperatuur toch door een computer moet worden verwerkt, ligt het voor de hand om de linearisering door de computer te laten verrichten. De meest eenvoudige manier (tenminste in een hogere programmeertaal) is het uitrekenen van de temperatuur met behulp van de benaderingsformule die we zojuist hebben gegeven. Als ook de snelheid van de temperatuurmeting van belang is, dan is het uitgebreide rekenwerk dat deze benadering vergt, waarschijnlijk te traag. Het aantal rekenkundige bewerkingen wordt drastisch beperkt en vereenvoudigd als we een aantal punten van de karakteristiek in een tabel opslaan en de computer daarmee laten rekenen.

In figuur 4 is de basiskonfiguratie van een digitaal meetsysteem getekend. Het zal u misschien verbazen dat de NTC ook hier van het lineariseringsnetwerkje is voorzien. Daar zijn twee redenen voor. Om te beginnen moet de NTC (een passieve komponent) van een voeding worden voorzien om iets te kunnen meten. Vaak wordt daar dan een brugschakeling voor genomen (in dit geval is dat dus een halve brug). Verder heeft het exponentiële verloop van de weerstand nadelige gevolgen op de nauwkeurigheid van de D/A-omzetting, immers een stapje van een bit vertegenwoordigt een temperatuurvariatie die afhangt van de steilheid van de karakteristiek, dus de nauwkeurigheid van de omzetting varieert ook.

In figuur 5 en 6 hebben we dat in beeld gebracht. Een voordeel van de digitale benadering is in ieder geval dat het temperatuurbereik niet wordt beperkt zoals bij de analoge benadering. De kromme delen worden toch recht gerekend.

Fig 5
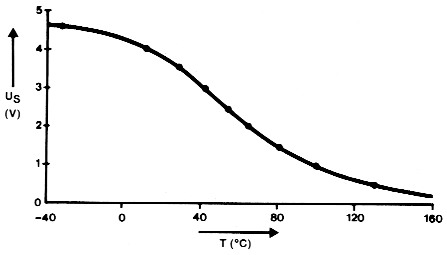
Figuur 5. Het uitgangssignaal (U_s) van het NTC netwerkje uit figuur 4.

Fig 6
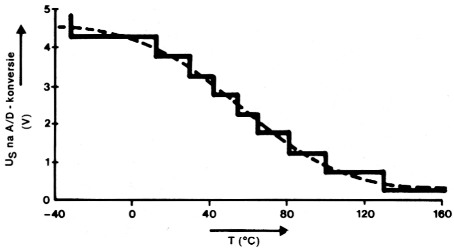
Figuur 6. De kurve uit figuur 5, maar nu getekend zoals die er na een A/D-konverter uit ziet.

In figuur 5 is het signaal te zien dat de A/D-omzetter uit figuur 4 krijgt aangeboden. Na de A/D-konversie ziet deze karakteristiek er bijvoorbeeld uit zoals is getekend in figuur 6. Goed te zien is, dat - zelfs bij een gelineariseerde NTC - ieder stapje een andere "hoeveelheid" temperatuur vertegenwoordigt, hetgeen natuurlijk minder wordt naarmate de stapjes kleiner worden.

Fig 7
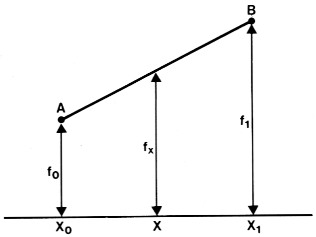
Figuur 7. Met lineaire interpolatie kan uit een tabel met beperkte omvang toch voldoende nauwkeurig de gemeten temperatuur worden berekend.

Het digitaliseren van een karakteristiek

Dit is eigenlijk niets anders dan het noteren (in het computer-geheugen) van de temperatuur bij een bepaalde spanning op een aantal plaatsen van de karakteristiek. In tabel 1 is dit gedaan voor 10 punten, met de grafiek uit figuur 5. Hoeveel punten worden opgeslagen in de computer hangt af van de gewenste nauwkeurigheid. Het meest nauwkeurig is het opslaan van een temperatuur voor iedere uitkomst van de A/D-konversie, maar dat kan aardig oplopen. Bij gebruik van een 8-bits-konverter moeten er 2⁸ = 256 waarden worden opgeslagen. Afgezien van de praktische bezwaren is het meestal ook voor de nauwkeurigheid niet nodig zoveel meetpunten op te slaan. Met minder meetpunten kan het ook. De tussenliggende waarden worden dan berekend (geinterpoleerd) door de computer.

De meest eenvoudige manier van interpoleren is lineaire interpolatie. Hierbij wordt verondersteld dat tussen twee bekende punten de grafiek een rechte lijn is (figuur 7). Een tussenliggende funktiewaarde (f_X) laat zich dan uitrekenen met de formule:

f_x = f_o + (x - x₀)
(f₁ - f_o) / (x₁ - x₀)

Als we het nu slim aanpakken, dan kan het rekenwerk tot een minimum worden beperkt. Dat begint bij het opstellen van de tabel. Als we er voor zorgen dat de "afstand" tussen de meetpunten - de grootte van dit interval wordt in de formule aangegeven met de faktor (x₁ - x₀) - konstant is (in tabel 1 is dat 0,5 V), dan kan deze faktor als konstante worden geprogrammeerd. Als we er dan verder ook voor zorgen dat het aantal waarden dat de A/D-omzetter kan meten (256 bij 8 bits) een veelvoud is van het aantal intervallen dat in de tabel is vastgelegd, dan wordt het rekenwerk nog eenvoudiger. Echt eenvoudig wordt het als ook nog rekening wordt gehouden met het talstelsel waarin wordt gerekend. De uitkomst van de A/D-konversie (een getal van enkele cijfers) wordt dan verdeeld in een meest signifikant deel en een minst signifikant deel. Het meest signifikante deel (het voorste cijfer(s) van het getal) geeft dan aan welke fabelwaarden we nodig hebben; het minst signifikante deel is het verschil x - x₀. Dit alles is het best uit te leggen met een voorbeeld.

Tabel 1.
U_s (V)	interval nummer	temperatuur (°C)
0	0	220
0.5	1	130.61
1	2	99.36
1.5	3	80.84
2	4	66.69
2.5	5	54.30
3	6	42.27
3.5	7	29.18
4	8	12.14
4.5	9	-32.81
5	10	-150,00

In tabel 2 hebben we als voorbeeld een programma in Pascal afgedrukt. De uitgangspunten van het programma zijn tabel 1 en een A/D-omzetter die decimale getallen van 0 tot en met 999 produceert. Dat lijkt misschien wat vreemd, maar dat is zo gekozen omdat 10 (het aantal intervallen) en 1000 (het aantal mogelijke konversieuitkomsten) "passen" bij het talstelsel, het tientallige. In de praktijk zullen dit meestal waarden zijn die "passen" bij het binaire stelsel, met andere woorden de waarden zijn machten van twee.

Terug naar het voorbeeld: Van de drie cijfers die de uitkomst van de A/D-omzetting vormen, geeft het eerste cijfer dus aan in welk interval x ligt (INTERVAL_NR) en de twee laatste cijfers geven aan waar x in het interval ligt ten opzichte van x₀ (x - x₀). In een hogere programmeertaal komen de voordelen van deze methode niet volledig tot hun recht, maar in een machinetaal-programma is op deze manier het bepalen van het interval waarin x ligt en het bepalen van (x - x₀) bijzonder eenvoudig. Het verdelen van de uitkomst van de konversie in een meest signifikant deel (INTERVAL NR) en een minst signifikant deel (x - x₀) wordt namelijk gerealiseerd door x respektievelijk een aantal malen naar rechts te schuiven en door de meest signifikante bits van x met een AND-operatie "nul" te maken. De fabelwaarden zijn dan door middel van geindexeerde adressering uit de tabel te vissen. De hiervoor benodigde instrukties behoren tot het standaardrepertoire van bijna iedere microprocessor en vergen geen uitgebreide rekenroutines.

Tot slot nog iets over de nauwkeurigheid van de interpolatie. In figuur 8 is de afwijking van de werkelijke karakteristiek getekend, als er wordt geinterpoleerd met behulp van tabel 1. Met name in het stuk van 1 tot 4 volt is de nauwkeurigheid ruimschoots voldoende. De nauwkeurigheid verbetert naarmate het aantal fabelwaarden groter wordt.

Fig 8
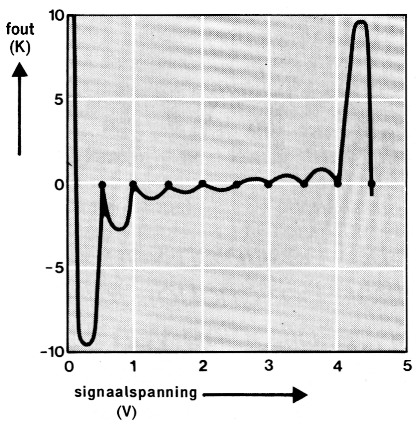
Figuur 8. De nauwkeurigheid van de interpolatie met tabel 1 ten opzichte van de "echte" kurve (figuur 5).