Der Antennenkoppler ohne Rollspule

Hochpass T-Glied mit zweiseitiger Schaltspule 1
Antennenkoppler gibt es wie Sand am Meer, in den verschiedensten Schaltungen und Ausführungen, für hohe und niedrige Leistungen, für symmetrische und asymmetrische Leitungen, in Billigbauweise und in Luxusausführung. Die allermeisten von ihnen bedienen sich einer verbderlichen Induktivitat in Form einer Rollspule. Und da fängt das Problem an: Rollspulen sind keine gängige Ware, sie sind nicht so leicht zu beschaffen. Von ihrer sehr geringen elektrischen Güte Q wollen wir hier ganz schweigen.
Die Flohmärkte sind meist leer gefegt, und die Fachhändler verlangen saftige Preise. Da ist es kein Wunder, wenn sich der noch selbst bauende Funkamateur eine andere Lösung herbei wünscht. Die einzig gangbare Alternative ist es, die Spule nicht kontinuierlich abzugreifen, sondem schrittweise abzuzapfen. Damit haben wir sofort den Umschwung von der Analogtechnik zur Digitaltechnik, wenn auch in einer ganz ungewohnten Weise. Die dazu verwendeten Schaltelemente sind simple Mehrfachschalter, die natürlich die Spannungen und Strome der Hochfrequenz aushalten müssen.
Die Aufwartsanpassung mit einem L-Glied
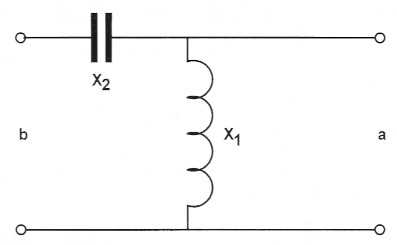
Bild 1: Das aufwarts anpassende L-Glied.
Wir sehen dazu das Bild 1. Der kleine Eingangswiderstand ist b, der große Ausgangswiderstand ist a. Beides sind Wirkwiderstände. Die im Längsweg liegende Kapazität hat den Blindwiderstand X2 die quer liegende Induktivität hat den Blindwiderstand X1. Weil a größer ist als b, wird aufwärts angepasst. Das Widerstandsverh¦ltnis bei der Anpassung ist m = a/b. Weil aufwärts angepasst wird, ist m größer als 1. Erfahrungsgemäß haben wir Schwierigkeiten, zu erkennen, auf welcher Seite der hohe und auf welcher Seite der niedrige Widerstand liegt. Das ist aber ganz einfach: X2 und X1 bilden einen "Serienschwingkreis" mit einer niedrigen Impedanz, deshalb liegt bei b der niedrige Widerstand. An der Spule X1 liegt dann der hohe Widerstand. Und noch etwas ist zu bemerken: Das L-Glied ist nicht in Resonanz mit der angepassten Frequenz; aber es ist nahe der Resonanz. Arbeitsfrequenz far die Anpassung und Resonanzfrequenz von Spule und Kondensator sind nicht identisch.
Aus den gegebenen Werten a, b, (und damit m) lassen sich die Blindwiderstände des L-Gliedes leicht berechnen [1; 2; 3]. Wir verwenden hier das computergerechte "SQR(x)" für "Quadratwurzel aus", um den Satz möglichst leicht lesbar zu gestalten. Wenn a und b gegeben sind, erhalten wir sofort m = a/b. Die Blindwiderstande sind dann:
X1 = + m × b/ SQR(m-1)
X2 = -b × SQR(m-1) {1}
Das + bedeutet einen induktiven Blindwiderstand, das - bedeutet einen kapazitiven Blindwiderstand. Wenn uns such noch die Frequenz gegeben wird, so lassen sich leicht die Induktivität und die Kapazität der X-Größen berechnen. Wir wollen jedoch aus den gegebenen Blindwiderständen X berechnen, welches Widerstandsverhältnis m damit zu erreichen ist. Damit kommen wir in die Praxis, wo gefragt wird: Was können wir auf 3,5 MHz mit einem Drehko von 10 pF bis 1000 pF und einer Spule von 2 µH anpassen, wenn der Eingangswiderstand 50 Ω betragt? Die Lösung bekommen wir durch die Berechnung der Verhältniszahl m. Und das geht so:
X1 = + m × b / SQR(m-1)
SQR(m-1) = m ×b / X1
X2 = -b × SQR(m-1)
SQR(m-1) = -X2 / b
Wir subtrahieren auf beiden Seiten das mathematisch spröde und wenig zuvorkommende Glied SQR(m-1) und setzen die Reste gleich!
m × b / X1 = -X2 /b
m × b × b = -X1 × X2
b2 × m = -X1 × X2
Damit wird das Anpassverhiiltnis:
m = -X1 × X2 / b2 {2}
Dabei ist m > 1 und somit -X1 × X2 > b2. Dies nennt man die Diskriminante der Gleichung. Bei m = 1 hört die Wirkung der Schaltung auf. Ist m kleiner als 1, so ist eine Anpassung unmöglich. Das ist in der Praxis der Fall, wenn man am Tuner verzweifelt herumkurbelt und -schaltet; aber das SWR will und will nicht auf 1 zurück gehen.
Eine weitere Vereinfachung
Wir schauen uns {2} an und erinnern uns, dass X1 = XL = ωL ist. In gleicher Weise ist X2 = XC = -1 / ωC. Dann muss sein: -XL × XC = ωL / ωC. Das ω kann herausgekürzt werden, and es ergibt sich: -XL × XC = L/C. Dabei werden L in Henry und C in Farad gemessen. Rechnen wir auf µH und pF um, so wird:
m = 106 × LµH / (b2 × CpH)
Daraus konnen wir für die Praxis eine zugeschnittene Größengleichung für 50 Ω Eingangsimpedanz machen:
m = 400 × LµH / CpF {3}
Eine praktisches Beispiel der Aufwartsanpassung
Nehmen wir das Beispiel von oben: Eingang 50 Ω, 2 µH, 10-1000 pF bei 3,5 MHz. Damit wird der Anpassfaktor nach {3}:
m = (106 × 2 µH) / (2500 × 10 pF) = 80 (für 10 pF) und
m = (106 × 2 µH) / (2500 × 1000 pF) = 0,8 (für 1000 pF).
Dieses letzte Ergebnis ist nicht möglich; denn wir wollten ja eine Aufwärtsanpassung, und wissen von der Diskriminante, class m immer größer als 1 sein muss. Dies entspricht: X1 × X2 > 2500. Wir hätten freilich such nach {2} rechnen konnen, und hätten das gleiche Ergebnis erhalten, nur ware dies wesentlich umstandlicher geworden.
Eine kleine Vergleichsrechnung zeigt, class bei C2 = 800 pF die Grenze erreicht ist; denn dort wird m = 1, und darunter geht es nicht. Schon an dem ersten Beispiel mit m = 80 sehen wir, dass das Anpassverhältnis m recht hoch ist, and dies gilt allgemein für die Anpassungen mit L-Gliedern. Leider ist es mit gangigen Bauteilen oft zu hoch, oder der Abstimmvorgang ist sehr kritisch, so dass wir zu erweiterten Schaltungen greifen müssen.
Die Diskriminante als Diagramm
Um es so bequem wie möglich zu machen, haben wir den wichtigen Wert der Diskriminante in zwei Diagrammen mit hoher Genauigkeit dargestellt. So kann bei der praktischen Anwendung jeder beliebige Wert mit dem Zirkel abgegriffen werden. Als Eingangswiderstand werden 50 Ω zu Grunde gelegt, ganz einfach weil heute der Gerateausgang auf diesen Wert genormt ist. Damit wird der Wert der Diskriminante -X1 × X2 = b2 oder -X1 × X2 = 2500. Dieser Wert ist in Bild 2 als schrager Balken dargestellt. Für aufwarts anpassende L-Glieder sind alle Konfigurationen rechts vom Balken moglich, links vom Balken sind sie nicht moglich. Als Ausgangsgrößen stehen die beiden Blindwiderstande X1 (induktiv) and X2 (kapazitiv) in Ohm an den Außenleisten. Ihr Produkt muss größer sein als 2500, sonst kann die Anpassung nicht funktionieren. Das dazu gehorige, günstige Feld liegt rechts vom Balken.
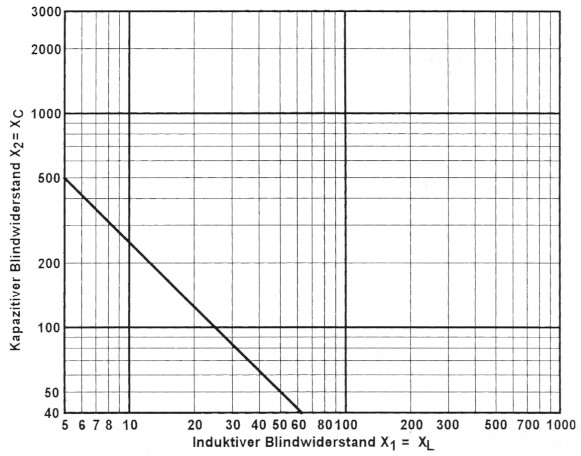
Bild 2: Tapete für Blindwiderstande mit der Diskriminante als Grenze.
Auch der versierteste Praktiker hat kein sicheres Gefühl für die Größe von Blindwiderständen. Wir haben uns deswegen die Mühe gemacht, die Blindwiderstände in Induktivitäten und Kapazitäten umzurechnen und diese mit größer Genauigkeit in ein Diagramm umgeformt (Bild 3). Auf der linken, senkrechten Skala sind die Kapazitäten des Kondensators dargestellt. Achtung: Die Skala steht auf dem Kopf! 10 pF sind oben and 1000 pF stehen unten. Die Induktivität der Spule ist unten horizontal und normal dargestellt. Das heißt, sie verlauft von links nach rechts. Als Werte wurden für Spule und Kondensator allgemein gängige Größen verwendet. Auch hier ist der verboten Bereich links unter dem Balken. In diesem Dreieck ist die Diskriminante kleiner als 2500 und es kann nicht angepasst werden. Mit diesem Diagramm sparen wir uns die umständliche Berechnung von X1 and X2 and deren Multiplikation. Es wird also alles viel einfacher. Nehmen wir uns jetzt das obige Beispiel her: Eine Anpassung war mit 2 µH und 800 pF gerade noch möglich. Wir verfolgen die waagerechte 800-pF-Linie nach rechts und schneiden die Diskriminante genau bei 2 µH.
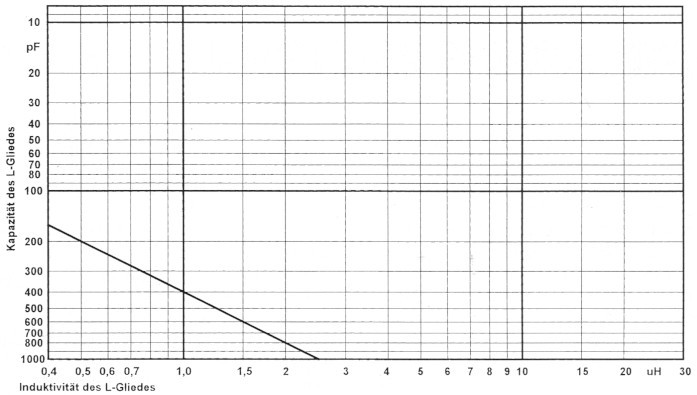
Bild 3: Tapete für Kapazität und Induktivität mit Diskriminante als Grenze.
Ganz bestimmt werden kritische Leser hier sofort einwenden: Wo bleibt denn die Frequenz? Die ist ja überhaupt nicht angegeben! Das stimmt; denn um die Diskriminante zu bestimmen, kann man auf die Frequenz verzichten. Deswegen lässt sich dieses Diagramm bei allen Frequenzen der kurzen Wellen ohne weiteres verwenden. Der Beweis ist einfach aus {3} zu erbringen. Auch dort ist die Frequenz verschwunden, und deswegen sind die Diagramme für alle Frequenzen brauchbar. Das sogenannte L/C-Verhaltnis bekommt also hier eine ganz neue Bedeutung. Für VHF und UHF müssen wir nur die Diagramme nach links und nach oben erweitern, also von 10 pF zu 1 pF und von 1 µH zu 1 nH gehen.
Die Abwartsanpassung mit einem L-Glied
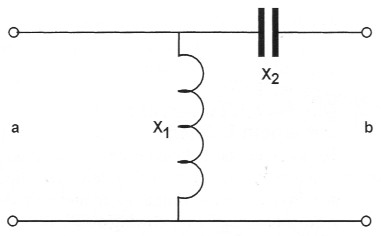
Bild 4: Das abwärts anpassende L-Glied.
Schalten wir das L-Glied each Bild 4, so wird von a nach b herab transformiert. An a liegt nämlich die hochohmige Spule und an b der niederohmige "Serienschwingkreis". Well der größe Anpasswiderstand a und der kleine Anpasswiderstand b gegeben sind, erhalten wir sofort das Widerstands-Anpassverhältnis m = a/b. Damit wird b = a/m, was wir noch brauchen werden. Die Blindwiderstande von Spule (X1) und Kondensator (X2) werden dann:
X1 = +m × b / SQR(m-1) und
X2 = -b × SQR(m-1) {4}
Das Minuszeichen besagt, dass der Kondensator eine negative Reaktanz bildet. Bild 4 zeigt einen Hochpass. Bei einem Tiefpass müssten wir lediglich die Spule gegen den Kondensator, also X1 gegen X2 vertauschen, womit sich nur die Vorzeichen nicht aber die Größen ändern würden. In den kommenden Termen beschränken wir uns nur noch auf a, ersetzen also b durch a/m und erhalten:
X1 = (m × a/m) / SQR(m-1)
X1 = a / SQR(m-1)
X2 = -a x SQR(m-1) / m
-X2 × m / a = SQR(m-1)
Jetzt eliminieren wir das Schwierigkeiten bereitende SQR(m-1):
SQR(m-1) = a / X1
SQR(m-1) = -X2 × m / a
Beide Seiten werden gleich gesetzt, es gibt:
a / X1 = -X2 × m / a
Damit wird das nach unten transformierende Anpassverhältnis, dem wir zur Unterscheidung einen Strich beifügen:
m' = a2 /(-X1 × X2) {5}
Well SQR(m'-1) nur dann reell ist, wenn der Wert unter der Quadratwurzel > 0 ist, muss m' > 1 sein. Deswegen wird a2 > (-X1 × X2). Wir haben hier wiederum eine Diskriminante. Diesmal ist es jedoch umgekehrt: Das Produkt aus den beiden Blindwiderständen muss kleiner sein als das Quadrat des Eingangswiderstandes. Dieser Umstand mutet etwas fremd an. Wir können uns aber diesen Tatbestand an Bild 4 klar machen. Der kleine Eingangswiderstand a liegt an der hochohmigen Spule. Um richtig anzupassen muss die Impedanz X1 ziemlich niedrig sein. Also ist auch das Produkt -X1 × X2 recht klein, auf alle Fälle kleiner als a2. Auf den Diagrammen der Bilder 2 und 3 ist jetzt der verboten Bereich über und der erlaubte Bereich unter der schragen Grenzlinie.
Das m' aus {5} lasst sich wie oben noch weiter vereinfachen zu:
m' = (a2 × CpF) /(106 × LµH)
Daraus können wir abermals eine für 50 Ω Eingangsimpedanz zugeschnittene Größengleichung machen:
m' = CpF / (400 × LµH) {6}
Ein praktisches Beispiel der Abwartsanpassung
Wir verwenden die gleichen Werte wie bei der Aufwärtsanpassung: Eingang 50 Ω, Spule 2 µH, Drehkondensator 10-1000 pF, Frequenz 3,5 MHz. Damit wird der Anpassfaktor nach {6}:
(für 10 pF): m' = 10 pF / (400 x 2 µH) = 0,0125
(für 1000 pF): m' = 1000 pF/ (400 x 2 µH) = 1,25
Der erste Wert stimmt offensichtlich nicht; dem er darf nur größer als 1 sein. Also stimmt allein der zweite Wert m = 1,25. Die Diskriminante verlangt aus den Blindwiderstanden für 2 µH und 1000 pF X1 = 14 π; X2 = 103 / 7 π: a2 > -X1 × X2.
Das heißt: 2500 > 14 π 103 / 7 π. Dies entspricht: 2500 > 2000 und ist daher richtig. Weil hier eine Abwärtsanpassung vorliegt, müssen wir etwas umdenken: Es geht von 1,25 auf 1 and das ist:
1/m' = 1 : 1,25 = 0,8. So ist der abwarts transformierte Widerstand das 0,8-fache des Eingangswiderstandes, und das sind 40 Ω.
Jetzt schauen wir schnell im Diagramm des Bildes 3 nach: 1000 pF und 2 µH, das liegt unter der schragen Diskriminantengrenze. Es geht! 10 pF und 2 µH, das liegt weit über der Grenze. Das geht nicht!
Um die Grenze zu finden, wo m' = 1 ist, setzen wir X1 × X2 = 2500. Die Spule von 2 µH ist fest, sie hat X1 = 14 π, also kann nur der Drehko verandert werden. Mit 1000 pF ist er zu groß, er müsste kleiner gestellt werden. Daher ergibt sich: X2 = 2500 / π = 56,84 Ω, die wir dann in pF umrechnen können. Bei 3,5 MHz sind dies exakt 800 pF, der gleiche Wert übrigens, den wir such bei der Aufwärtstransformation erhalten haben. Schauen wir in Bild 3 nach: 800 pF und 2 µH, das liegt genau auf der Grenze. Es geht gerade noch!
Einfacher ist die Berechnung von m' für den letzten Fall each {6}:
m' = 2500 × 800 pF /106 × 2 µH = 1.

Karl H. Hille, DL1VU.