Velocityfactor/verkortingsfactor
Naar aanleiding van het verzoek, of was het een uitdaging aan aspirant artikelschrijvers, een antwoord te geven op het hoe en waarom van de "verkortingsfactor" meetmethode zoals beschreven in de noot bij het artikel "antenneversterking" deel 2 van PA0OOO in CQ-PA nr. 12, heb ik gemeend een antwoord te moeten geven waarbij een geringe hoeveelheid Transmissielijntheorie onvermijdelzjk bleek.
De theorie mag tevens een bijdrage leveren tot een beter begrip van het zo "raadselachtige" kabelgedrag.
Transmissielijntheorie
De karakteristieke impedantie Zk
Zk is de ingangsimpedantie van een oneindig Lange lijn welke opgebouwd gedacht kan worden door een oneindig aantal secties achter elkaar geplaatst.
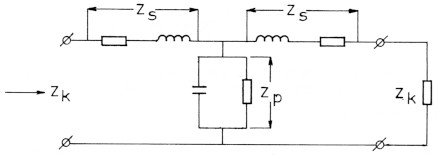
Fig. 1.
![]()
Ingangsimpedantie ![]() (1)
(1)
Praktisch is R << WL en G << WC, zodat ![]() welke ohms en frequentie onafhankelijk is.
welke ohms en frequentie onafhankelijk is.
De voortplantingskonstante
![]() (2)
(2)
De voortplantingskonstante γ zegt ons iets over het gedrag en de kwaliteit van een kabel. De konstante is een complex getal en bestaat dus uit een reeel en een imaginair deel welke geschreven kan worden als:
γ = α + jβ
waarbij:
α de dempingskonstante is uitgedrukt in dB of Neper per lengte-eenheid en
β de fasekonstante uitgedrukt in radialen per lengte-eenheid.
Vaak wordt alleen het reële gedeelte α (de kabeldemping) als belangrijkste parameter van een kabel opgegeven.
Daar we hier de frequentie-afhankelijkheid van een lengte kabel bekijken, moeten we β verder uitwerken.
Voor iedere golflengte (λ) verplaatsing langs een lijn hebben we tevens 2×π rad. of 360° faseverschuiving.
In formule: ![]() (3)
(3)
Substitueren we λ met de algemene formule voor golfverschijnselen, V = f × λ , dan krijgen we:
![]() (4)
(4)
De factor β bevat dus een frequentieafhankelijke en een snelheidsafhankelijke komponent. De snelheid V is de snelheid van een elektromagnetische golf door een medium (lucht, teflon, polythelene, etc.).
De ingangsimpedantie Zi
De ingangsimpedantie van een netwerk wordt bepaald door de momentele spanning Û to delen door de momentele stroom î voor zowel de kabel als de belasting. De uitgewerkte formule is ook bier weer complex:
![]() (5)
(5)
waarbij:
Zl = de complexe belastingsimpedantie
1 = de lijnlengte
Zk = de karakteristieke lijnimpedantie
Zi = de complexe ingangsimpedantie
Lecherlijnen
Indien we het speciale geval van een open of een kortgesloten lijn bekijken (de zgn. Lecherlijnen), dan kunnen we de ingangsimpedantie als funktie van de factor β1 plotten in een grafiek.
De formule 5 ingevuld voor een kortgesloten lijn (Zl = 0) geeft ons:
![]()
De ingangsimpedantie is imaginair, d.w.z. zuiver inductief of capacitief afhankelijk van de factor βl.
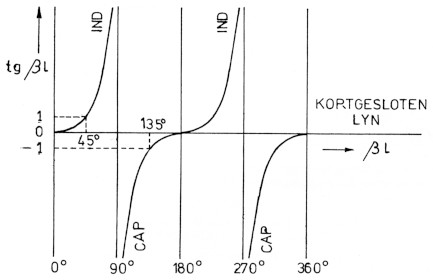
Fig. 2.
De formule 5 ingevuld voor een open lijn (Zl = ∞) geeft ons:
![]()
We zien als we ons beperken tot een open Lecherlijn dat:
Zi is capacitief voor 0 < l < ¼λ
Zi is 0 en ohms voor l = ¼λ + n × ½λ
Zi is inductief voor ¼λ < l < ½λ
Zi is ∞ voor l = 0 + n ×½λ
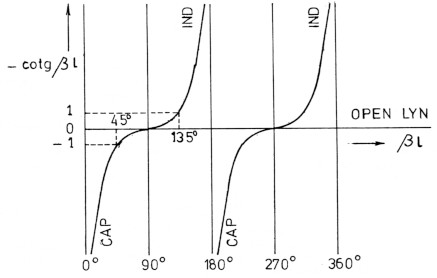
Fig. 3.
Wat gebeurt er nu indien een open coaxlijn van 75 cm lengte op een dipmeter aangesloten wordt. We zullen een dip dus een belasting van de dipmetertrillingskring konstateren.
Kijken we nu in het bovenstaande lijstje, dan blijkt dat dit optreedt indien de lijn λ lang is. Blijkbaar is de lijn in serieresonantie (max. belasting) voor een frequentie welke behoort bij een golflengte welke 4 maal de 75 cm lijnlengte is.
Hierbij nemen we even aan dat de snelheid van het signaal de lichtsnelheid heeft, de "Velocityfactor" is dan per definitie 1.
De frequentie is dan:
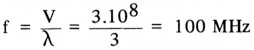
De snelheid van een signaal door een medium wordt echter bepaald door de dielektrische constante ε en de permeabiliteit μ van het medium volgens de formule:
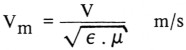
waarbij:
Vm = signaalsnelheid door het medium
V = lichtsnelheid in vacuum 2,99776.108 m/s
In een coaxiale kabel is het medium het dielectricum welke fungeert als afstandhouder voor de binnenader t.o.v. de buitenmantel.
Dit dielectricum zorgt voor een vertraging van het signaal waardoor we de frequentie van de dipmeter moeten verlagen om de formule weer kloppend te maken.
Indien we bijvoorbeeld een dip meten bij 66 MHz, dan is de snelheid van het signaal:
![]()
De verhouding van de snelheid door het medium en de snelheid door vacuum/lucht is per definitie de velocityfactor.
In dit voorbeeld:
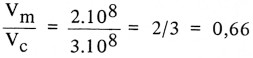
We zien hier inderdaad dat de velocityfactor overeenkomt met de frequentie van de dip-meter. Dat dit zo mooi uitkomt is vanwege het feit dat de gekozen werkelijke lengte van de kabel bij een mooie ronde frequentiewaarde (100 MHz) gecalibreerd is voor een velocityfactor van 1.
In Principe kan deze "truuk" echter bij elke willekeurige kabellengte en/of frequentie gebruikt worden door de theorie op de juiste wijze toe te passen.
Volgens de theorie moeten er nog meer frequenties zijn waarbij de 75 cm kabellengte een dip geeft op de dipmeter, nl. indien 75 cm overeenkomt met ¼λ + n×½λ, waarbij n een integer getal is.
Indien we ons houden bij een kabelvelocityfactor van 0,66, dan zullen er ook op de frequenties 200 MHz, 333 MHz, enz. dippen optreden.
Lecherlijnen zoals hier besproken vinden alom toepassing in zendinstallaties voor het onderdrukken van ongewenste even harmonische en in afstemeenheden als afstemelement. Praktisch wordt hoofdzakelijk gebruik gemaakt van de kortgesloten Lecherlijn, daar een kortsluiting beter gedefinieerd is dan een open lijn.
De gebruikte Engelse term "Velocityfactor" (snelheidsfactor) komt beter overeen met het eigenlijke mechanisme van het verschijnsel terwijl de normaal gebezigde Nederlandse term "Verkortingsfactor" meer het gevolg aanduidt.
Met beide termen wordt echter precies hetzelfde bedoeld.
Simon, PA0SJG.