Rob's web

Eenvoudige berekening zelfinductie van in een laag gewikkelde spoelen

Wij zendamateurs hebben (meestal) een hekel aan rekenen, helemaal als het gaat om relatief gecompliceerde formules zoals die bij zelfinductie gehanteerd moeten worden…

We pakken liever een spoelvorm en een klos draad, schatten het aantal wikkelingen met een timmermansoog en bepalen met de probeer-methode of de zelfinductie goed zit!

PAoBJG helpt ons tijd en koperdraad te besparen met de hierna beschreven methode en grafieken, waarbij het rekenwerk tot een minimum wordt teruggebracht.

In de literatuur vinden we voor het berekenen van de zelfinductie voor eenlaagsspoelen de volgende formule:

Eq 1

waarin:
L = zelfinductie in microhenry
n = aantal windingen
r = inwendige straal van de spoel in mm
1 = bewikkelde lengte van de spoel in mm

Mijn ervaring is dat hiermee vrij nauwkeurig de zelfinductie berekend kan worden.

Een nadeel is echter het rekenwerk, vandaar dat ik geprobeerd heb deze formule in een andere vorm te gieten.

Vervangen we r door (waarin d = inwendige spoeldiameter in mm), dan kunnen we bovenstaande uitdrukking herleiden tot

Eq 2

delen van teller en noemer door d levert

Eq 3

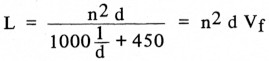
waarin

Eq 4

We zien dat deze term alleen afhangt van Eq 5, dus van de geometrie van de spoel en we duiden deze aan met vormfactor Vf.

Voor een aantal waarden van Eq 5 heb ik deze vormfactor berekend en in grafiek gezet (grafiek 1). Daar het gebruik van deze enkele grafiek niet voldoende nauwkeurige aflezing waarborgt heb ik het geheel opgesplitst in drie afzonderlijke grafieken (2 t/m 4).

Fig 1

Fig 2

Fig 3

Fig 4

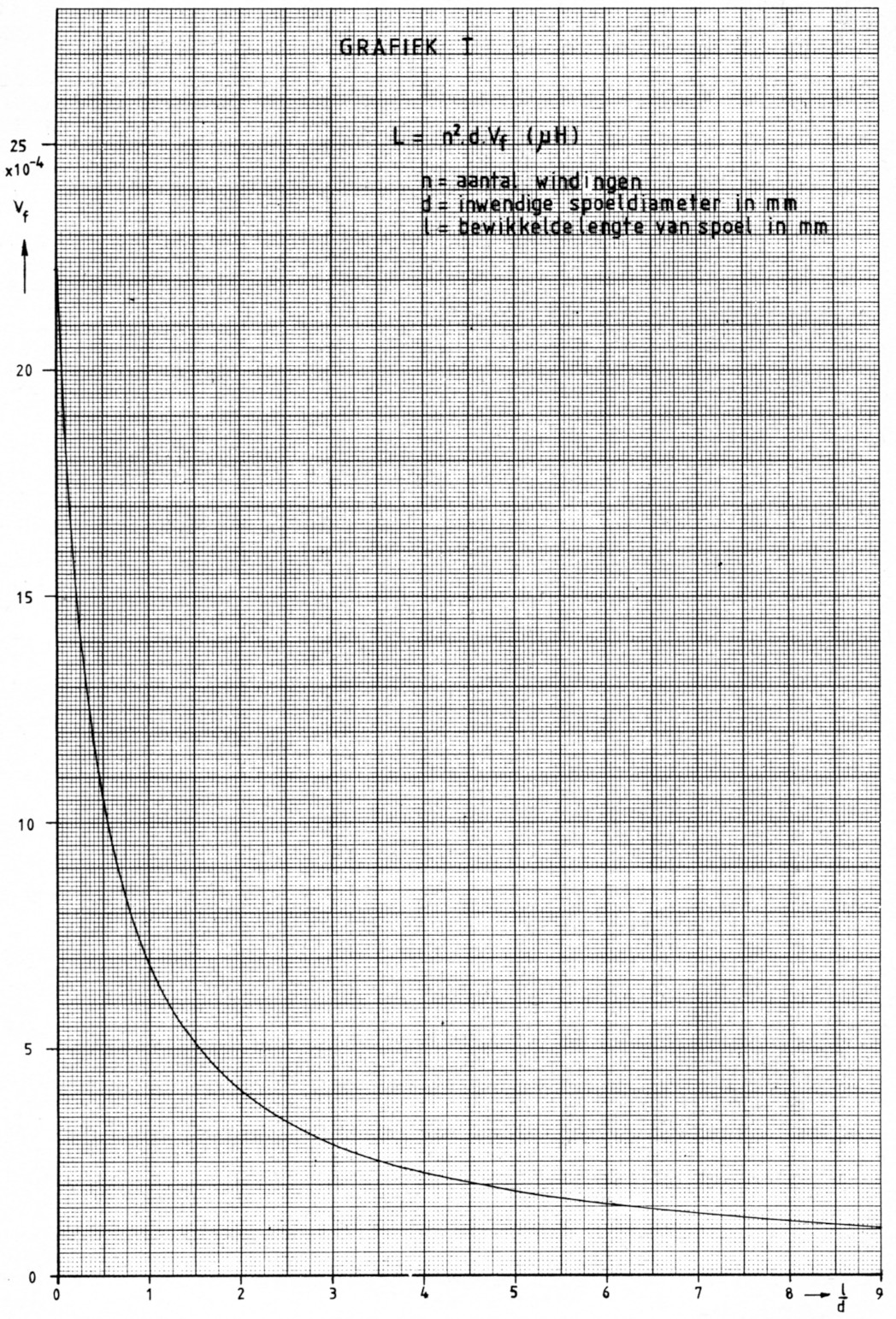
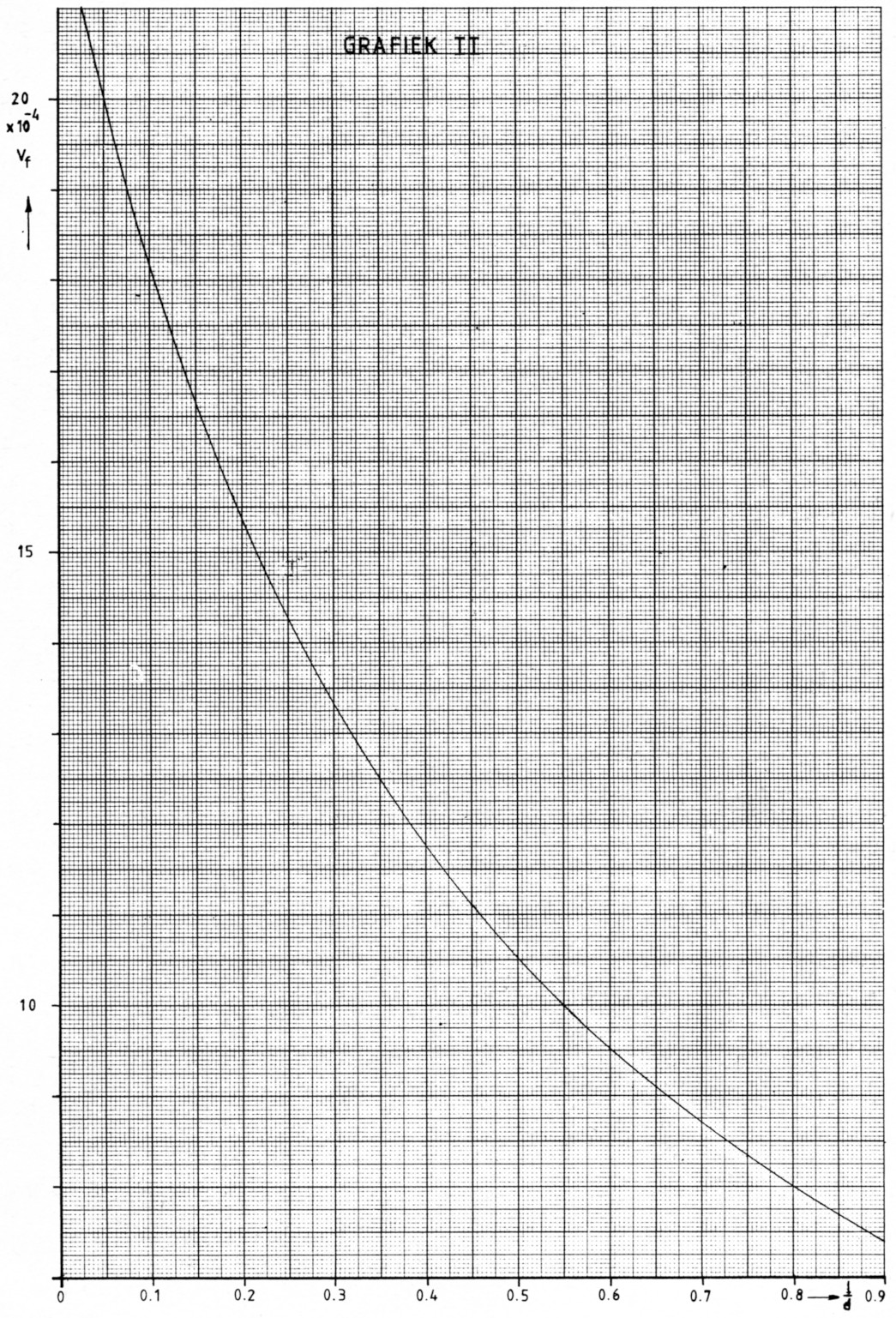
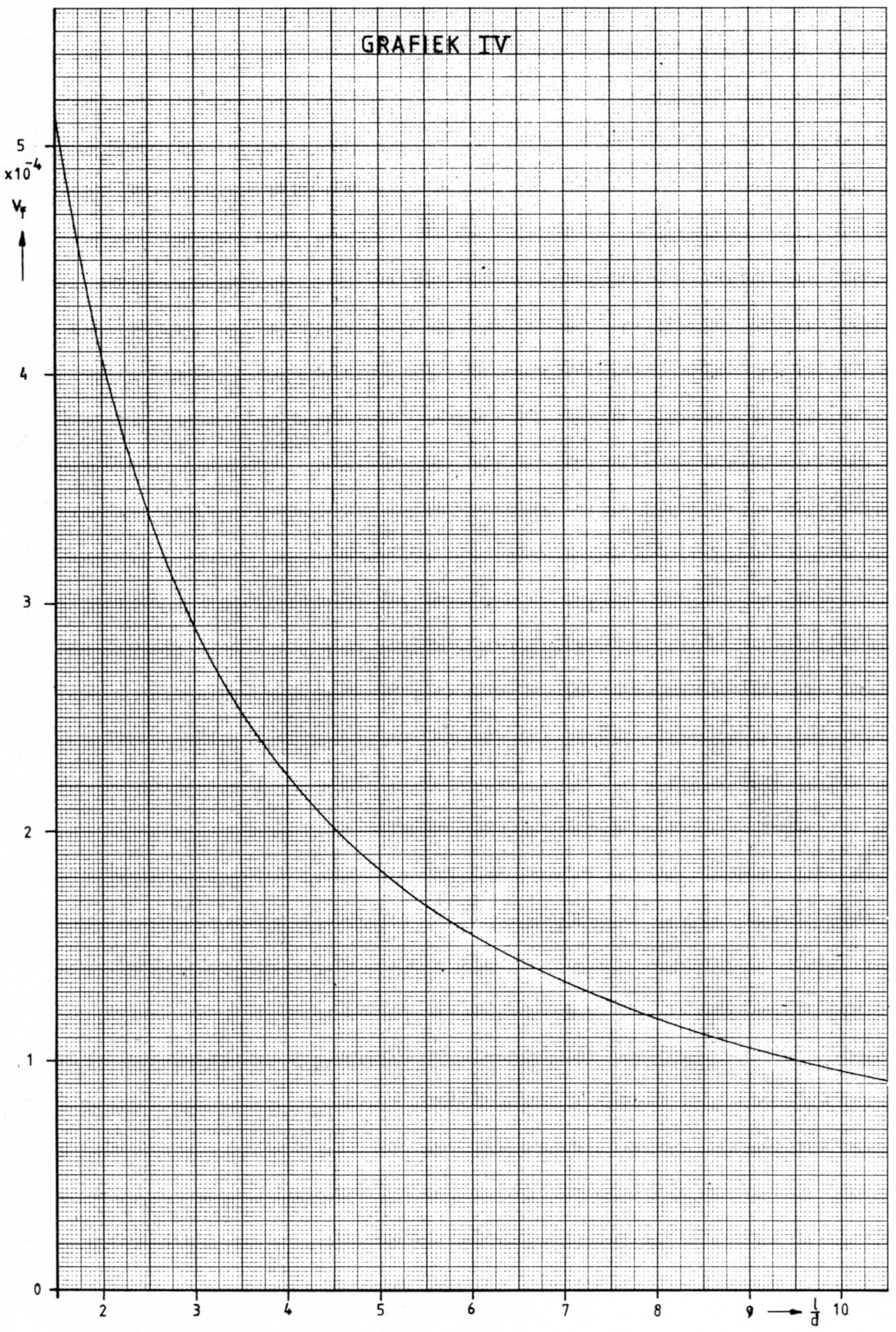
Om nu een spoel te berekenen bepalen we eerst de gewenste Eq 5 verhouding en lezen dan uit een van de grafieken de waarde van de vormfactor Vf af. Denk om de macht 10-4!

Kies die grafiek die het meest nauwkeurig af te lezen is.

Vermenigvuldiging van de gevonden factor met het kwadraad van het aantal windingen en de inwendige spoeldiameter in mm levert rechtstreeks de gevraagde zelfinductie in µH.

Voorbeeld

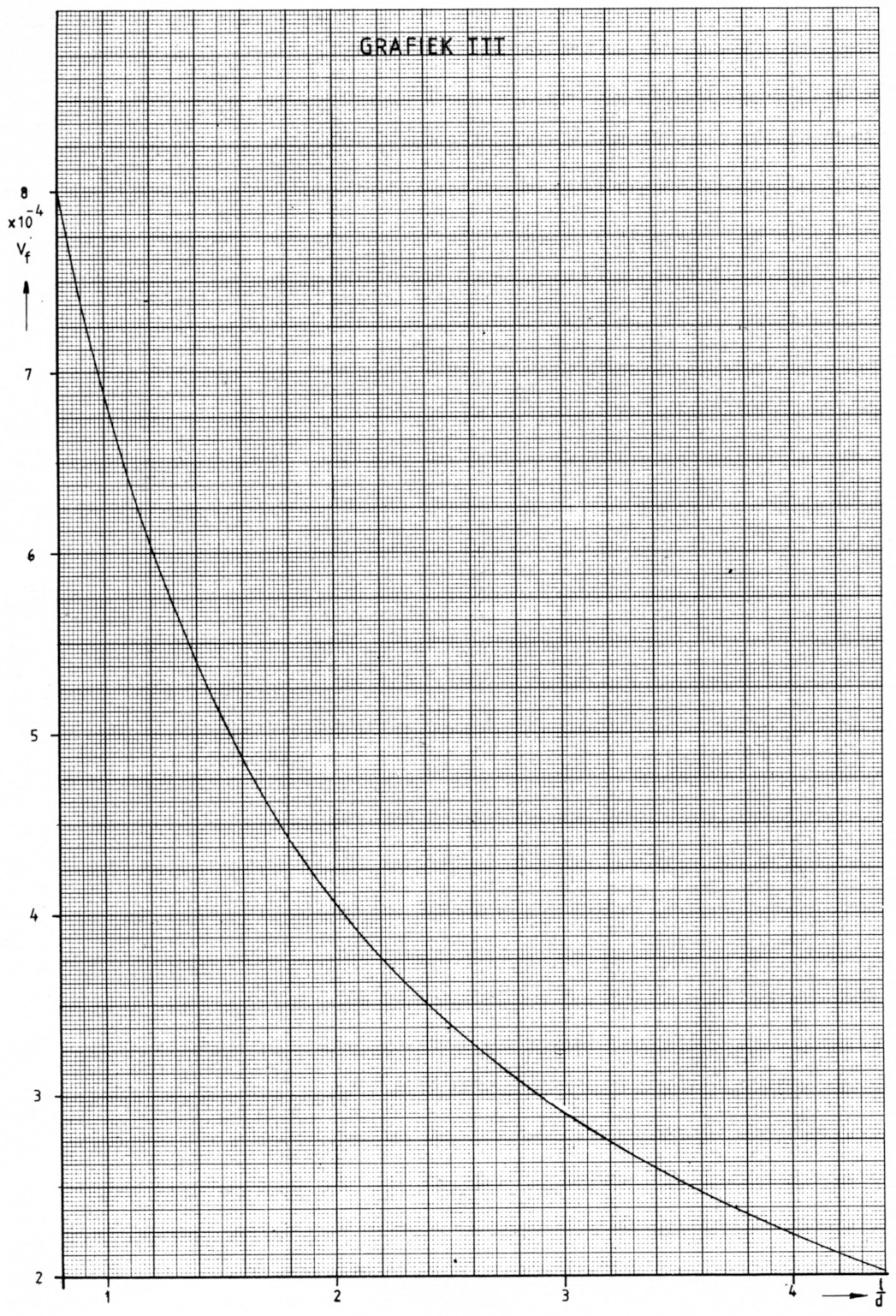
Hoe groot is de zelfinductie van een spoel van 10 windingen, een inwendige diameter van 8 mm en een Eq 5 van 2?

In grafiek 4 (eventueel 3) vinden we Vf = 4,08 × 10-4.

L = n2dVf = 102 × 8 × 4,08 × 10-4 = 0.326 µH

Omgekeerd is het ook mogelijk door keuze van een 1/d verhouding een vormfactor uit de grafiek te bepalen en het aantal windingen voor een gewenste zelfinductie te berekenen uit

Eq 6

PA0BJG.