De achtergrond van tropo DX 1. Voortplanting van de radiogolven in de troposfeer
De zeldzame tropocondities van eind november 1979 zullen bij de VHF en UHF enthousiastelingen nog lang in herinnering blijven. Het verkeer op de banden was vergelijkbaar met dat op 10 meter, waarbij vrijwel geen leeg plekje meer te vinden was.
Dit gebeuren was voor mij aanleiding om eens nader naar het hoe en waarom te kijken. In de voor de doorsnee amateur ter beschikking staande literatuur (een goed overzicht is te vinden in het VHF UHF Manual van de RSGB) wordt evenwel op deze zaken erg summier ingegaan.
In dit eerste artikel wordt de golfvoortplanting in de troposfeer besproken. De troposfeer is de onderste, ca 12 km dikke laag, van de atmosfeer. Het zal blijken dat terugbuiging naar het aardoppervlak optreedt wanneer lagen met een grote gradient in de brekingsindex in de troposfeer aanwezig zijn; het meest effectief werken ze wanneer ze dicht bij het aardoppervlak liggen.
In een tweede artikel wordt het ontstaan van zulke lagen behandeld en wordt het een en ander toegelicht aan de hand van een analyse van de weertoestand gedurende de periode van uitzonderlijk goede condities, eind november 1979.
Breking van elektromagnetische straling
Zoals algemeen bekend plant elektromagnetische straling, waartoe o.m. behoren zichtbaar licht en radiogolven, zich rechtlijnig voort wanneer het medium niet van samenstelling verandert. De snelheid is het grootst in vacuum (de lichtsnelheid c is dan 3×109 meter per seconde), in een ander medium is de snelheid kleiner en geldt dat de snelheid v = c/n waarin n de brekingsindex is.
In vacuum is n precies gelijk aan 1; voor zichtbaar licht is de brekingsindex in water 1,33 en in lucht van normale temperatuur en druk ligt de waarde van n zeer dicht bij 1. De brekingsindex in een bepaald medium hangt ook of van de golflengte van de straling, maar eenvoudigheidshalve zullen we steeds spreken van licht, ook wanneer we straling met grote golflengte (radio straling) bedoelen.
Wanneer licht het grensvlak tussen twee media passeert (b.v. het grensvlak lucht en water) is er een verandering van de voortplantingsrichting. Kwantitatief is het verband tussen de richtingen voor en na de passage van het grensvlak gegeven door de wet van Snellius die zegt dat: n I sin al = n2 sin a2, waarin al en a2 de hoeken zijn die de richtingen maken met de loodlijn op het grensvlak (fig. 1).
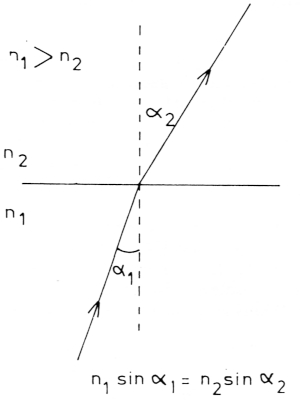
Fig. 1.
Een bijzonder geval treedt op wanneer de lichtstraal vanuit het optisch dichtere medium (dat met de grootste brekingsindex) een steeds grotere hoek (αl) maakt met de loodlijn op het grensvlak; de hoek α2 neemt toe volgens de gegeven wet tot α2 negentig graden wordt. Wanneer αl dan nog groter wordt treedt totale reflectie op: de lichtstraal dringt niet meer door in het optisch dunner medium maar reflecteert a.h.w. tegen het grensvlak (fig. 2). De hoek α1 waarbij dit juist gebeurt wordt gegeven door de voorwaarde dat n1 sin αl = n2.
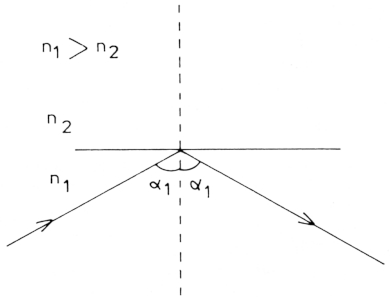
Fig. 2.
Afbuiging van licht in een brekingsindex-gradient
We nemen nu het geval dat de brekingsindex continu verandert; we kunnen dan niet meer spreken van een scherp grensvlak tussen de media als boven is verondersteld. Met deze situatie hebben we bij de golfvoortplanting in de atmosfeer in feite steeds to maken, maar daarop gaan we verderop nader in.
We bekijken het volgende voorbeeld. Een lichtstraal valt vanuit een medium met brekingsindex n1 op een laag waarin de brekingsindex continu met de dikte van de laag varieert van ni tot n2. De dikte van de laag is d. Aan de bovenzijde van de laag veronderstellen we de brekingsindex weer overal dezelfde (fig. 3). Binnen de laag is er een brekingsindex-gradient, d.w.z. een verandering van n per lengte eenheid (b.v. per meter), aangeduid met Δn / Δl (Δs) slaan op veranderingen). We noemen de brekingsindex-gradient kortweg grad n en voor het bovenstaande geval is grad n = (n1 - n2) / d binnen de laag overal dezelfde. Grad n heeft ook een richting, n.l. loodrecht op de beide grensvlakken met de gebieden waar n constant is of met andere woorden grad n is een vector (heeft zowel grootte als richting).
Elektromagnetische strafing plant zich in een medium met grad n niet rechtlijnig voort zoals in een medium waarin n constant is (grad n = 0). De lichtweg is gekromd (fig. 3); de afwijking van de rechte lijn is zodanig dat buiging optreedt naar de plaats met groter brekingsindex.
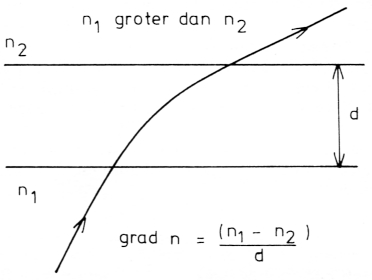
Fig. 3.
Dit gaan we kwantitatief na, maar eerst iets over het begrip kromming. In fig. 4 is in een punt van de kromme lijn de kromme zo goed mogelijk benaderd met een stukje cirkelomtrek. De lijn PM die het punt P met het middelpunt van de cirkel (M) verbindt is de kromtestraal; het omgekeerde van de kromtestraal noemt men de kromming. Zo kan men voor elk punt van een kromme lijn de kromming kwantitatief weergeven. De kromtestraal van de aarde is dus gelijk aan de straal van de aarde (= 6410 km) en de kromming op het aardoppervlak is Z = 1/R = 156 × 10-9 per meter.
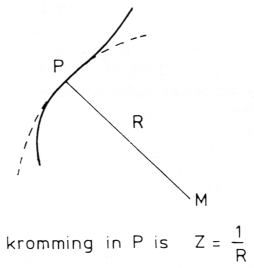
Fig. 4.
Men kan nu bewijzen dat in een medium met een gradient in de brekingsindex de kromming in een punt van de lichtweg gelijk is aan Z = (sin α . grad n) / n waarin α de hoek tussen de raaklijn aan de lichtweg en de richting van gradient n. Het middelpunt van de cirkel met straal R = 1/Z ligt op de loodlijn op de raaklijn en de drie richtingen, grad n, raaklijn S en de straal PM liggen in een vlak (fig. 5).
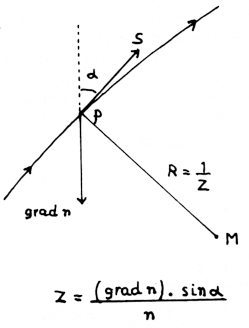
Fig. 5.
Het exact berekenen van een lichtweg in een medium met grad n is zeer gecompliceerd maar voor enkele gevallen (fig. 6) zijn eenvoudige regels to stellen:
- Voor de weg aangegeven met (1) in fig. 6 geldt dat n1 sin αl = n2 sin α2, d.w.z. geheel analoog aan de breking over een scherp grensvlak tussen media met brekingsindices n1 en n2.
- Voor de weg aangegeven met (2) in fig. 6, waarbij er als het ware reflectie optreedt geldt voor de brekingsindex np op hoogte p boven het onderste grensvlak dat np = n I sin al (als bij een reflectie tegen een scherp grensvlak tussen media met brekingsindices n1 en np. Men kan gemakkelijk afleiden dat p = (1 - sin αl) / grad n.
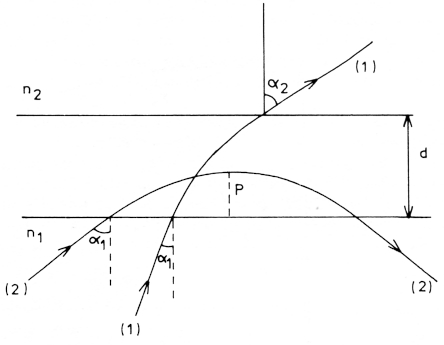
Fig. 6.
Toepassing op de voortplanting in de troposfeer
De brekingsindex van lucht ligt zeer dicht bij 1. Op het aardoppervlak is n ongeveer 1.00035 en op b.v. 3 km hoogte is n = 1.0002. Er bestaat een continu met de hoogte afnemende brekingsindex en grad n bedraagt dicht bij het aardoppervlak ca 40 × 10-9 per meter. Onder bijzondere omstandigheden kan zich in de troposfeer een laag van bepaalde dikte ontwikkelen waarin de gradient van de brekingsindex veel groter is dan bovengenoemde normale waarde. Dit is het geval in een z.g. inversielaag.
Het brekingsindex verloop in een dergelijke laag is weergegeven in fig. 7. Over het ontstaan van een dergelijke laag wordt in een volgend artikel gesproken.
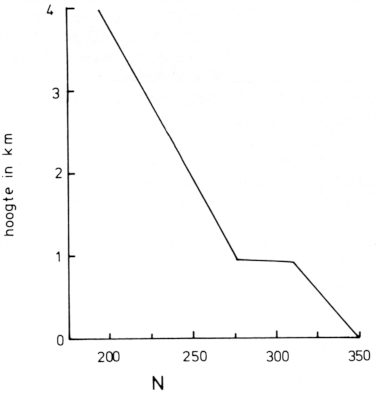
Fig. 7.
We gaan eerst na hoe het bereik van een zender wordt wanneer we kromming van de baan t.g.v. de normale brekingsindex-gradient in aanmerking nemen.
Dit wordt toegelicht in fig. 8. Een zender bevindt zich op hoogte H (= AD) boven het aardoppervlak. Bij rechtlijnige voortplanting is het bereik tot B (waar de lijn AB raakt aan het aardoppervlak). Doordat de weg gekromd is wordt het punt C bereikt; het stuk AC is een deel van een cirkelomtrek.
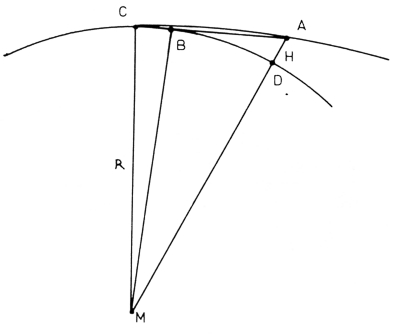
Fig. 8.
We hadden gezien dat normaal grad n = 40 × 10-9 per meter, waardoor de kromming van de lichtweg berekend uit Z = sin α × grad n / n met alfa vrijwel 90° en n vrijwel gelijk aan 1 wordt 40 × 10-9 per meter, hetgeen correspondeert met een kromtestraal van 25000 km dus ca 4 maal zo groot als de straal van de aarde. Men berekent eenvoudig dat AB = √2.H.R terwijl AC = √2.H.R.(11-R/R1); R is de kromtestraal van de aarde, R1 die van de lichtweg.
De maximaal te bereiken afstand is dus niet veel groter dan bij rechtlijnige voortplanting!
Voortplanting bij aanwezigheid van inversielagen
Uit het bovenstaande volgt direct dat de omtrek van de aarde gevolgd wordt wanneer de gradient in de brekingsindex gelijk is aan 156 × 10-9 per meter, de kromming van de aarde. Deze waarde van de gradient is ca vier keer zo groot als de normale waarde.
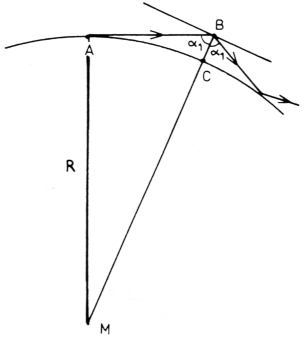
Fig. 9.
We nemen nu eerst het hypothetische geval van een grenslaag met een sprong in de brekingsindex. Deze grenslaag (fig. 9) bevindt zich op hoogte H (= BC) boven het aardoppervlak. Vanuit A wordt horizontaal (is evenwijdig aan het aardoppervlak) een golf uitgezonden en we nemen voor het gemak dat tussen A en B de voortplanting rechtlijnig is.
Voor totale reflectie moet gelden dat sin α1 = n2/n1. We zien ook dat sin α1 = R/(R + H) waaruit volgt dat ni/n2 = 1 + R/H. Met H = 100 meter is ni/n2 = 1.000016, bij H = 1000 meter is n1/n2 = 1.000156.
Voor de sprong in de brekingsindices, n1 - n2, vindt men in het eerste geval 16 × 10-6 en in het tweede geval 156 × 10-6 (n.b. n1 - n2 is vrijwel gelijk aan n1/n2 - 1). Merk op dat de hoek a1 zeer dicht bij 90° ligt. We zien dat voor totale reflectie de vereiste sprong in de brekingsindex voor een laagliggende laag veel kleiner is dan voor een hogerliggende laag. We nemen nu het geval dat een inversielaag met dikte d zich bevindt op hoogte H. De vraag of de situatie van fig. 6 (1) (straling gaat in de ruimte verloren) of die van fig. 6 (2) zich voordoet hangt zoals bovenstaand beredeneerd is of van de grootte van de brekingsindexgradient, de dikte van de inversielaag en de hoek van inval.
We nemen een getallen voorbeeld: met d = 100 meter, grad n = 200 × 10-9 per meter (hetgeen correspondeert met een verschil van 20 × 10-6 in de brekingsindex onder en boven de laag) krijgen we terugbuiging naar het aardoppervlak wanneer de invalshoek ligt tussen 89,6 en 90°. Wanneer de invalshoek kleiner is dan 89,6° is de terugbuiging onvoldoende en gaat de straling in de ruimte verloren.
Bij een laagliggende inversielaag (d.w.z. dicht bij het aardoppervlak) is de hock van inval dicht bij 90° en zullen we dus meer kans hebben op terugbuiging naar het aardoppervlak dan bij een hogerliggende laag (aangenomen dat de gradient en de dikte dezelfde is voor beide gevallen) waarbij de hoek van inval verder van 90° afligt. We zien dit direkt uit fig. 9.
Omdat de hoek waarover de terugbuiging plaats heeft dicht bij 180° ligt zal het weinig uitmaken of we nu horizontaal dan wel verticaal gepolariseerde straling beschouwen. Bij reflectie tegen het aardoppervlak is het voordelig om horizontaal gepolariseerde straling te gebruiken, omdat hiervoor het reflectievermogen van het aardoppervlak hoger ligt. Bij een laagliggende inversielaag kan het verschijnsel dat bekend staat als 'ducting' optreden. De golf wordt dan a.h.w. opgesloten tussen de inversielaag en het aardoppervlak. Dit legt een beperking op aan de golflengte, deze mag n.l. niet to groot zijn. Voor de maximale golflengte geldt dat t = 500λ 2/3 waarin t de hoogte van de laag en A de golflengte, beide in centimeters.
Dit houdt in dat voor een inversielaag op een hoogte van enkele honderden meters de golflengte ligt in het VHF en UHF gebied. Men kan zich voorstellen dat terugbuiging optreedt in de inversielaag, daarna reflectie tegen het aardoppervlak waarna weer terugbuiging etc. Tenslotte moet nog opgemerkt worden dat de hier gegeven beschouwing een geidealiseerde toestand betreft. Radiostraling afkomstig van onze antennes is nog wel iets anders dan de hier veronderstelde puntvormige lichtbron en ook de inversielagen zullen er wel gecompliceerder uitzien dan hier verondersteld is (b.v. niet altijd parallel aan het aardoppervlak en geen uniforme gradi8nt).
Deel 1 - Deel 2.
G.A. Wiegers, PE1BGU.