De staande-golf meter; goed of slecht
Een veel gebruikt maar slecht begrepen meetinstrument is de staande-golf meter (SWR-meter). Nu zijn er goede en slechte SWR-meters; dit artikel geeft inzage in het hoe en waarom en beschrijft een methode om te constateren in hoeverre onze eigen meter van onbespro ken gedrag is.
Hoe werkt een SWR-meter? Om dit eens en voor altijd duidelijk te maken, dienen we eerst de coaxkabel te belichten. Een SWR-meter is weliswaar ook te gebruiken voor niet-coaxiale voedingslijnen, maar de doorgaans in gebruik zijnde typen zijn hiervoor niet geschikt. Overigens is een SWR-meting aan een niey-coaxiale lijn meestal niet erg zinvol.
De spanning en stroom in een coaxkabel heeft een bepaalde verhouding. Deze verhouding is over de gehele lijn gelijk wanneer de coaxkabel met zijn karakteristieke impedantie wordt afgesloten. Deze verhouding U/I is dan precies gelijk aan de karakteristieke impedantie.
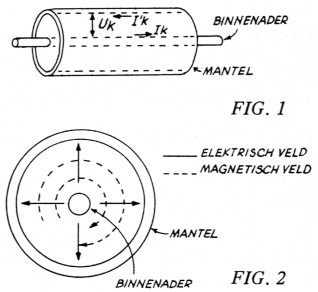
De stroom in de kabel bevindt zich aan de buitenkant van de binnenader, en aan de binnenkant van de mantel (skineffect), zie fig. 1. Het energie transport in de coaxkabel komt tot stand door het electro-magnetische veld, dat zich bevindt tussen de mantel en de binnenader. Dit is geschetst in fig. 2. De richting van het energietransport wordt aangegeven door de richting van de richting van de electrische en magnetische velden. Dit betekent dat de spanning en stroom een bepaalde richting hebben, afhankelijk van de richting van het energietransport. Op dit verschijnsel is de SWR-meter gebaseerd!
Bezien we nu de constructie van een SWR-meter als getekend in fig. 3. Weliswaar zijn er vele andere uitvoeringen in omloop, maar de werking is in principe steeds dezelfde. Er zijn twee factoren die de meteruitslag van M1 en M2 bepalen. Enerzijds is er een inductieve koppeling tussen de meetdraadjes, anderzijds een capacitieve. De inductieve koppeling introduceert een stroom, die via R wordt omgezet in een spanning. De capacitieve koppeling geeft eveneens een spanning op de meetdraden en de som van de beide spanningen wordt door de diode omgezet in een gelijkspanning. De som is dus C1 × Uk plus C2 × R × Ik, waarbij C1 en C2 de capacitieve en inductieve koppelfactoren voorstellen.
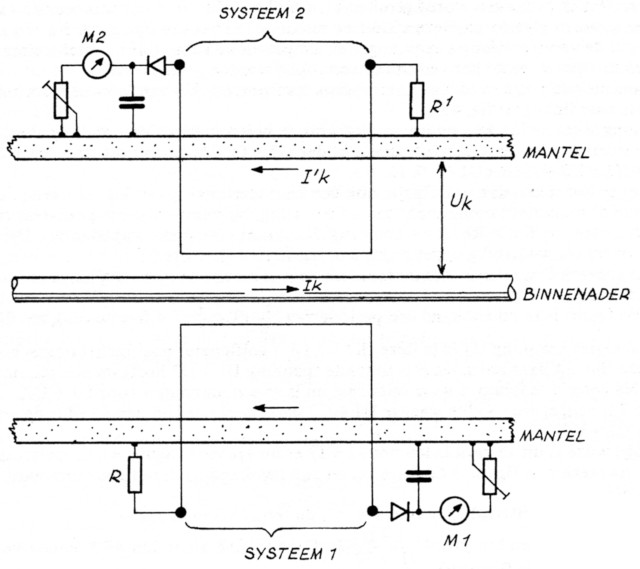
Fig. 3.
Veronderstel nu, dat er energietransport plaatsvindt van links naar rechts en dat de kabel is afgesloten met zijn karakteristieke impedantie. Er is dan alleen een energietransport van links naar rechts, en verder is er een bepaalde plaats onafhankelijke verhouding tussen de spanning en de stroom in de kabel. Verder kiezen we R zodanig, dat C1 × Uk = C2 × R × Ik. Meter M2 zal nu een uitslag vertonen, M1 echter niet. Dit komt, omdat de spanning t.g.v. Uk precies 180° uit fase is met C2 × R. Ik in meetsysteem 1. Het faseverschil tussen 1 en 2 is steeds 180°, immers, in feite is alleen het meetdraadje gewoon omgedraaid.
Wordt er nu energie de kabel opgestuurd aan de rechterzijde, en links de kabel afgesloten met de karakteristieke impedantie, dan zal M1 een uitslag geven en M2 niet.
Dus, de uitslag van M1 of M2 geeft aan, in welke richting er energietransport plaatsvindt. Tevens is de meteruitslag een maat voor het vermogen dat wordt getransporteerd. Men moet echter bijzonder voorzichtig zijn met het gebruik van de SWR-meter als vermogensmeter want dit is alleen haalbaar als de kabel karakteristiek is afgesloten, dus met zijn karakteristieke impedantie.
Een eenvoudig experiment kan dit illustreren. Maak maar eens met opzet een misaanpassing; de SWR-meter zal meestal in de stand "forward" iets anders aanwijzen. Overigens is dit een tekortkoming van de SWR-meter. De betere en dus kostbaardere SWR-meters vertonen dit verschijnsel niet!
Resumerend, de meteruitslag van M1 is een maat voor het vermogenstransport van rechts naar links, M2 geeft het vermogen aan van lins naar rechts. Door beide uitslagen te vergelijken hebben we inzicht in de verhouding van de beide vermogens.
Bij ons zendamateurs wordt het vermogen geleverd door een zender en wordt er een zeker vermogen gereflecteerd door de antenne. De meters M1 en M2 laten dan zien hoeveel (of hoe weinig) vermogen door de antenne wordt gereflecteerd.
Merkwaardig genoeg is de werking van een SWR-meter te illustreren zonder over staande golven te spreken. Dit is een gevolg van het feit dat de SWR-meter gebaseerd is op de zgn. "directional coupler" (richtingsgevoelige koppeling).
Het is echter interessant om te zien hoe een en ander in zijn werk gaat, wanneer er staande golven worden geihtroduceerd. Eerst een beschrijving van het staande-golf verschijnsel. Wanneer een coaxkabel (of een willekeurige andere transmissielijn) wordt afgesloten met een impedantie ongelijk aan zijn karakteristieke impedantie, ontstaat er een gereflecteerd vermogen. Dat er vermogen wordt gereflecteerd blijkt uit het feit, dat wanneer de kabel karakteristiek wordt afgesloten, deze afsluiting maximaal vermogen opneemt. Bij een andere afsluiting is de vermogensopname geringer en aangezien de kabel zelf meestal weinig of geen vermogen dissipeert, moet het verschil in vermogen worden gereflecteerd.
In de transmissielijn zijn er nu twee vermogens transporten, een van links naar rechts en een van rechts naar links (zie fig. 4).
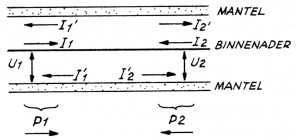
Fig. 4.
De spanning langs de lijn kan nu eenvoudig worden beschreven als de optelling van U1 en U2. Veronderstel, dat de reflectie zodanig is, dat U2 = C × U1, dan wordt de totaalspanning Ut: Ut = U1 + U2 = U1 + cU1 (C ≤ 1).
Men dient te bedenken dat de reflectie ook een faseverschuiving kan introduceren (n1. bij capacitieve of inductieve component van de belasting, bij ohmse belasting ontstaat er een sprong van 180° bij R1 > Rk, R1 = belasting, Rk = karakteristieke impedantie). Deze fasesprong kan echter wiskundig opgeborgen worden in de constante C.
Voor een gegeven C is nu een momentopname te maken van de spanning langs de lijn. Stel b.v. C = 0,5, zie figuur 5.
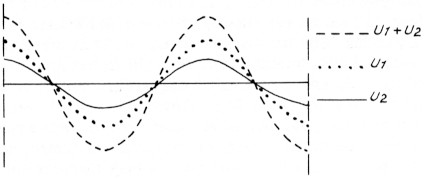
Fig. 5.
Een zelfde figuur is te tekenen, na een periode van ![]() (T = 1/f, f = frequentie), zie figuur 6.
(T = 1/f, f = frequentie), zie figuur 6.
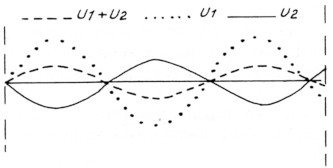
Fig. 6.
De sinusvormige spanning U1 is in deze tijd ¼λ (λ = golflengte) naar rechts opgeschoven, U2 in deze tijd ¼λ naar links. De resulterende spanning U1 + U2 heeft nu een minimum bereikt. Na weer ¼ is figuur 5 weer ontstaan, en is er een maximum voor U1 + U2. In figuur 7 is aangegeven welke waarde U1 + U2 maximaal aan kan nemen (dus de amplitude van U1 + U2).
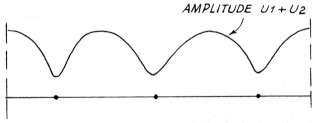
Fig. 7.
Op analoge wijze is uit te knobbelen hoe Il + I2 er uit zal zien (figuur 4). Er ontstaat dan figuur 8. Aangezien in figuur 8 de amplituden zijn getekend, is deze figuur uiteraard tijds onafhankelijk.
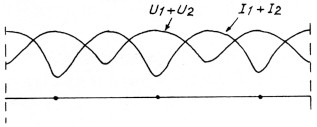
Fig. 8.
Deze tijds onafhankelijkheid is de oorzaak van de term "staande golven"!
In figuur 8 is te bepalen hoe groot ![]() is. Deze grafiek moet dan de dimensie van impedantie hebben (zie figuur 9).
is. Deze grafiek moet dan de dimensie van impedantie hebben (zie figuur 9).
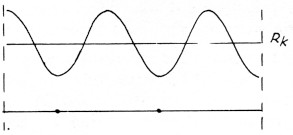
Fig. 9.
Deze impedantie grafiek blijkt rond de waarde Rk te slingeren. Betekent dit nu, dat op de snijpunten van deze grafiek met de lijn Rk de impedantie gelijk is aan Rk? Dit is niet het geval. Op deze snijpunten bestaat n.l. een faseverschil tussen de spanning en de stroom en er is dus een capacitieve of inductieve component op deze plaatsen.
Wat heeft dit nu voor gevolgen voor de SWR-meter? Om dit te illustreren kunnen we de spanning en stroom die in de meetdraadjes wordt geïmnduceerd het beste als vectoren geven (zie figuur 10 en 11).
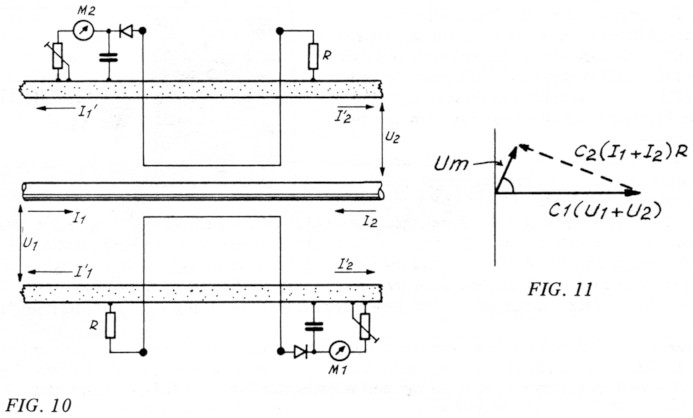
We zien in figuur 11 dat C1 (U1 + 12) in de meetleiding wordt verminderd met C2(I1 + I2)R Beide zijn echter vectoren, zodat er een verschil vector ontstaat, Um, die eventueel de meter kan doen uitslaan. Het aardige is nu, dat Um voor een gegeven waarde van de belastingsimpedantie een constante lengte heeft. Deze lengte of amplitude wordt via de gelijkrichter omgezet in een gelijkspanning.
Deze gelijkspanning heeft dus een constante waarde, ongeacht waar in de kabel de SWR wordt gemeten, of hoe lang de kabel is. Dit geldt alleen voor verliesvrije kabels! Wanneer we de SWR-meter denkbeeldig door de kabel schuiven, zal de SWR-meter dus steeds dezelfde SWR moeten aangeven. Het vectortje Um in figuur 11 draait hierbij rond, t.g.v. het veranderen van de vectoren (U1 + U2)C1 en C2(I1+I2)R.
In de praktijk blijkt dit echter niet of nauwelijks op te gaan. Dit is een gevolg van de constructieve tekortkomingen van de SWR-meter, het niet oneindig klein zijn van de meetdraadjes en het optreden van stroom langs de buitenkant van de SWR-meter.
Om een indruk te geven: een goede SWR-meter (b.v. van Bird) geeft bij een SWR van 1:2 waarden tussen de 1,8 en 2,2 en een goedkope SWR-meter geeft waarden tussen de 1,5 en 3! Een heel eenvoudige test kan de kwaliteit van een SWR-meter duidelijk maken. Hiervoor is nodig:
- Een stuk coaxkabel van 75 ohm, ¼ golflengte lang.
- Een stuk coaxkabel van 50 ohm, ⅛ golflengte lang.
- Een stuk coaxkabel van 50 ohm, ¼ golflengte lang.
- Een stuk coaxkabel van 50 ohm, ½ golflengte lang.
Hoe we een en ander in de praktijk gaan beproeven wordt duidelijk uit de opstelling getekend in figuur 12.
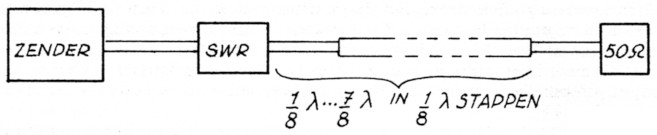
Fig. 12.
Het stuk kabel van 75 ohm, ¼λ transformeert de 50 ohm dymmyload naar ongeveer 100 ohm. Dit moet een SWR geven van 1:2. Door steeds de lengte kabel te varieren tussen deze 100 ohm en de SWR-meter, is een grafiekje te maken van de waarde die de SWR-meter aangeeft t.o.v. de werkelijke SWR van 1:2.
Wellicht dat deze test de relativiteit van een SWR-meting laat zien of een tot nu toe "vertrouwde" meter door de mand laat vallen. Door het grafiekje steeds bij de hand to houden kunnen we de meter-uitslag voortaan interpreteren en aflezen wat de werkelifIce SWR is.
PA0WOW.