Dbm, dB, dBc, dBA, dBmV, dBV, dBkW, dBW
De decibel is een rekeneenheid, die of en toe tot verwarring leidt. Het volgende artikel is bedoeld om enigszins duidelijkheid te scheppen. Voor iemand die niet gewend is met dB's en zijn verwanten te rekenen, zal dit artikel wellicht niet meteen het gemak aantonen van het rekenen met dB's. Misschien kan dit artikel dan dienen om het gebruik van dB's in andere artikelen op te helderen. Wellicht wordt de dB dan toch nog hanteerbaar.
Om iets over de decibel te kunnen zeggen, moet eerst verteld worden wat een logarithme is. De decibel en alle daarvan afgeleide vormen is n.l. een logarithmische maat.
Logarithmen
Het kan voordelen hebben om de logarithme te gebruiken wanneer de getallen waarmee gewerkt wordt erg groot of erg klein zijn, of wanneer er vaak wordt vermenigvuldigd of gedeeld.
Beide faktoren zijn in de telecommunicatie ruim vertegenwoordigd (denk b.v. aan "deze versterker versterkt 100 keer ", of "dat signaal is driemaal zo sterk als dit ", enz.).
Grote en kleine getallen worden geschreven in de zgn. exponentiele notatie. Neem b.v. 100.000. De exponentiele notatie is 1 × 105. Er zijn twee delen te onderscheiden. Ten eerste een getal tussen de 1 en 10, en tweede een 10 met een klein getalletje rechtsboven. Dit kleine getalletje is de "exponent". Deze exponent geeft aan, hoe vaak je het grondtal (hier 10) met zichzelf moet vermenigvuldigen. Vermenigvuldiging van beide delen (het eerste en het tweede) geeft het uiteindelijk resultaat.
Dus:
1 × 105 = 1 × 10 × 10 × 10 × 10 × 10 = 100000.
Een ander voorbeeld:
3,2 × 103 = 3,2 × 10 × 10 ×10 = 3200.
Is de exponent negatief, dan wordt het tweede gedeelte "een gedeeld door".
B.v.:
3,2.10-3 = 3,2. 1 = 32 (_ 2 10.10.10 10000 \ 625/Waarom al die moeite?
Het voordeel blijkt, wanneer de getallen vermenigvuldigd worden, of gedeeld.
B.v.: 3200- 3'2.103 = 3,2.103-10-5 = 3,2.10-2 100000 1.105Met deze mooie ronde getallen valt een en ander nog wel zonder exponentiele notatie te doen, maar probeer dit eens:
3650000000x 0,00032 78600Nu in exponentiele notatie:
3,65.109.3,2.10 3,65.3,2 109.10-4 3,65.3,2 • 109 7,86.104 7,86 104 7,86 3,65.3,2Het werkelijke rekenwerk is nu beperkt tot het uitrekenen van
Het is ook mogelijk om het eerste gedeelte van de exponentiele notatie als "tienmacht" te schrijven, dus net zo als het tweede gedeelte.
B.v.: 2.105 10°'3.105De getallen tussen 1 en 10 zijn in een tabel ondergebracht of m.b.v. een rekenmachine te vinden. De twee tienmachten die nu ontstaan zijn samen te nemen tot een, door de exponenten eenvoudig op te tellen, b.v.:
1. 2.105 = l0°'3.105 = 105'3 2. 5 .106 10°,7.106 = 106'7De gedachte achter de decibel is nu (zoals bij iedere logarithmische notatie) om alleen de exponent op te schrijven. Dit moet dan uiteraard wel aangegeven worden. Hiertoe dient de toevoeging "B". Deze nieuwe notatie bleek echter te grof voor gemakkelijk gebruik, dus werd (net zoals de decimeter) de decibel ingevoerd, afgekort de dB.
Het vinden van de exponent kan gebeuren d.m.v. een tabel of m.b.v. een rekenmachine. Hiertoe dient de toets "log". De logarithme van een getal is dus het vinden van de exponent. In het voorgaande is steeds het getal 10 gebruikt, waarbij een exponent moest worden gevonden. Er zijn natuurlijk ook andere getallen mogelijk, dit valt echter buiten het bestek van dit artikel.
Er kan nu worden gedefinieerd wat de omzetting van een getal in dB's wordt.
dB = 10 × log A.
Hierbij is A het getal wat omgezet wordt.
Ter illustratie volgen hier een aantal voorbeelden.
Het begrip dB en alle daarvan afgeleide rekeneenheden dienen ter vergelijking van twee vermogens, b.v. uitgangsvermogen van een versterker Los. het ingangsvermogen, het signaalvermogen t.o.v. het ruisvermogen, e.d.
In een klein aantal gevallen is de spanningsverhouding aan de orde, b.v. in lijnsystemen. Om de zaak echter niet nodeloos te compliceren, blijft dit even buiten beschouwing.
De decibel geeft dus een vermogensverhouding aan. Voor het getal A dient deze verhouding te worden ingevuld. We krijgen dan:
dB = 10.1og -P1 P2 IIOp deze manier kan de versterking van een eindtrap b.v. opgegeven worden als 6 dB.
P1Dit betekent (zie tabel A) dat -P2 = 4, dus de vermogensversterking bedraagt 4x.
| A → dB (ongeveer) | |
|---|---|
| 2 | 3 |
| 4 | 6 |
| 5 | 7 |
| 10 | 10 |
| 100 | 20 |
| 1 | 0 |
| 0,5 | -3 |
| 0,1 | -10 |
| 0,01 | -20 |
Omdat de dB een verhouding aangeeft, is het onmogelijk om een bepaald vermogen te koppelen aan het aantal dB's. De invoering van de dB had echter een zodanig succes, dat de behoefte ontstond om ook absolute vermogens, en niet alleen verhoudingen, m.b.v. dB's te schrijven. De procedure hiertoe is eenvoudig, er wordt gewoon afgesproken wat het referentievermogen wordt. M.a.w.: P2 in vgl. II wordt vastgelegd. De dB gaat nu over in een andere notatie, waarin dit referentievermogen genoteerd staat, zie tabel B.
| referentievermogen (P2) | notatie |
|---|---|
| 1 mW (= 0,001W) | dBm |
| 1 W (= 1 W) | dBW |
| 1 kW (= 1000 W) | dBkW |
Voor een vermogen kan ook -U2 worden geschreven.
Vergelijking II wordt dan:
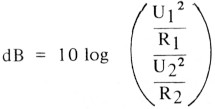( U12 \ R dB = 10 log U22 IIIAls nu geldt R1 = R2, dan2volgt:
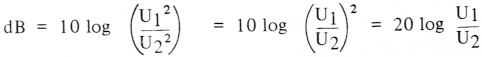
dB = 10 log (U1 = 10 log (U1)2 = 20 log U1 U22 U2 U2De laatste stap ligt niet direkt voor de hand, maar het voert hier te ver dit toe te lichten.
Deze laatste vorm, dB = 20 log U - is de grondslag voor een aantal andere "dB vormen".
Hierbij wordt nu een referentiespanning i.p.v. een referentievermogen gebruikt, zie tabel C.
| referentiespanning | notatie |
|---|---|
| µV | dBµV |
| mV | dBmV |
| V | dBV |
Er zijn nu nog twee dB-vormen ongenoemd, de dBA en dBc. De dBA heeft als referentie het nog net hoorbare geluidsniveau. Het is dus een acoustische rekeneenheid.
De dBc is een vorm met als referentie het draaggolf (carrier) vermogen. Hiermee kan dus eenvoudig b.v. onderdrukkingen t.o.v. het draaggolf niveau worden aangegeven.
Praktische rekenvoorbeelden
De meest voorkomende rekengrootheden in de telecommunicatie zijn de dB, dBc en dBm. Dit artikel zal zich hiertoe dan ook beperken.
Als eerste dient opgemerkt te worden, dat de dB een vermogensverhouding aangeeft, terwijl de dBm een vermogensniveau aangeeft. Bij het rekenen met dB's en dBm's is het volgende van belang.
Wanner men de "gewone" getallen vermenigvuldigt , worden de dB's opgetelt. Delen komt overeen met aftrekken.
Om eenvoudig te kunnen werken met de dB's en dBm's wordt hier nog even een tabel gemaakt van enerziids de vermenigvuldigfactoren en anderzijds de bijbehorende dB waarden.
Hoe kunnen nu tussenliggende waarden worden gevonden? Het eenvoudigst kan dit d.m.v. een rekentuig, zie hiervoor het theoretisch gedeelte.
Vaak is echter een schatting voldoende nauwkeurig. Dit kan als volgt gebeuren:
Stel dat de bedoeling is om een vermenigvuldigfactor om te zetten in dB's. Splits hiertoe deze factor in een produkt, waarvan de factoren min of meer in tabel D terug te vinden zijn. Vervolgens wordt het aantal dB's per term opgeteld.
B.v.: de om te zetten factor is 40.
Dit is te schrijven als 4 × 10.
Dus 40 = 4 × 10 = 6 + 10 dB = 16 dB.
Een versterker met een vermogensversterking van 40 x geeft dus 16 dB versterking. Een ander voorbeeld:
5000000 = 5 × 1000 × 1000 = 7 + 30 + 30 dB = 67 dB.
Bij verzwakking is de procedure geheel gelijk, echter het aantal dB's wordt van een minteken voorzien.
B.v.: Een mixer verzwakt 10 ×. Hoeveel dB's is dit?
10 × = 10 dB + de mixer geeft -10 dB versterking.
De werkwijze om van dB's naar een vermenigvuldigfactor te komen is als volgt:
Splits het aantal dB's in een optelling, waarbij de afzonderlijke termen in de tabel D terug kunnen worden gevonden. De termen worden stuk voor stuk omgezet en met elkaar vermenigvuldigd.
B.v.: 37 dB = 30 + 7 dB = 1000 × 5 = 5000 ×.
Een station, dat 37 dB sterker is dan een ander, produceert dus een 5000 maal groter vermogen aan de ingang van de ontvanger.
Bij dBm's is de werkwijze geheel analoog. Hierbij is de uitkomst echter geen losse vermenigvuldigfactor, maar een vermogen dat te vinden is door 1 mW met de gevonden vermenigvuldigfactor te vermenigvuldigen.
| factor | dB's |
|---|---|
| 1 | 0 |
| 2 | 3 |
| 4 | 6 |
| 5 | 7 |
| 10 | 10 |
| 100 | 20 |
| 1000 | 30 |
| 10000 | 40 |
B.v.:
Hoe groot is een vermogen van 30 dBm?
30 dB = (zie tabel D) 1000 ×. 1000 × 1 mW = 1 W.
Het vermogen is dus 1 W.
Hoe groot is -20 dBm?
20 dB = 100 ×. -20 dB = gedeeld door 100,
dus -20 dBm = 1 mW gedeeld door 100 = 0,01 mW = 10 µW.
Op analoge wijze kan de dBc worden gebruikt. Hierbij heeft de vermenigvuldigfactor echter betrekking op het draaggolfvermogen.
B.v.: Een zender produceert een draaggolf met een ongewenste component op -40 dBc.
Wat wil dit zeggen? 40 dB = 10000 ×. De ongewenste component bevat dus 10000 maal minder energie dan de draaggolf. Heeft de draaggolf een vermogen van 100 Watt, dan heeft de ongewenste component een vermogen van
100 = 10 mW. 10000Bij wijze van afsluiting wordt een blokschema behandeld van een ontvanger, waarbij aan de ingang van een bepaald ingangssignaal aanwezig is, zie fig. 1.
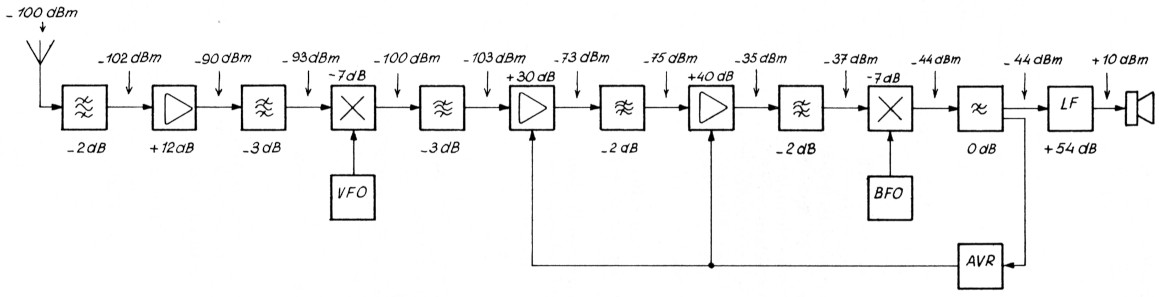
Uiteraard is dit slechts een schets. Het voordeel van dB's en dBm's moge uit dit voorbeeld blijken. Om een inzicht te krijgen in de verdeling van de versterking en verzwakking in een ontvanger, en de diverse signaalniveaus, is slechts de versterking in dB's per trap nodig. Een aangenomen ingangssignaal is daar eenvoudig te volgen door de gehele ontvanger.
PA0WOW.