Plaatsbepaling van de maan
In de eerste CQ-PA van 1983 stond een oproep om een eenvoudige tabel te produceren, waaruit de richting en de hoogte boven de horizon van de maan afgelezen kan worden. Zo'n tabel bestaat echter niet; de beweging van de maan aan de hemel is daarvoor te ingewikkeld. Met grote rekenmachines en tegenwoordig computers lukt dit wel. Toch was er vroeger reeds een behoefte om te weten waar de maan aan de hemelbol staat, bijvoorbeeld bij astronomen en zeelieden. In astronomische almanakken (Nautical Almanac, Kalender flir Sternfreunde), staan tabellen, waaruit we met enige achtergrondkennis de plaats van de maan op de hemelbol kunnen bepalen. Het doel van dit verhaaltje is nu, om ook nietastronomen enige van deze trucjes te leren. Met een catalogus kunnen we dan alles berekenen. Het is ondoenlijk om hele rissen tabellen hier weer te geven; ik beperk me daarom tot zes dagen rond het perigeum (het punt van dichtste nadering tot de aarde).
Enige opmerkingen vooraf. In dit verhaaltje worden graden en boogminuten enerzijds en uren en minuten anderzijds door elkaar gebruikt. Goniometrische functies van uren zijn niet getabelleerd; ook een rekenmachine weigert zo'n argument. Voor zover dit van toepassing is, moeten we uren in graden omrekenen. 24 uur komt overeen (A) met 3600, ofwel 10 ≡ 4m. Verder gelden de basisgegevens voor Oh GMT, dus niet in lokale tijd.
Ruwe lijnen
We willen om "a" uur GMT de maan vinden.
- Bepaal de lokale sterretijd "LST".
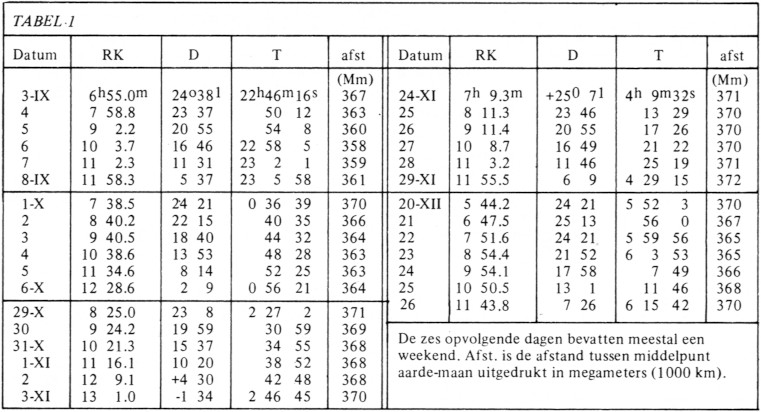
- Bereken de rechte klimming "RKL" om "a" uur met behulp van tabel 1.
- Bereken de uurhoek "t".
- Bereken de declinatie "dn" om "a" uur uit tabel 1.
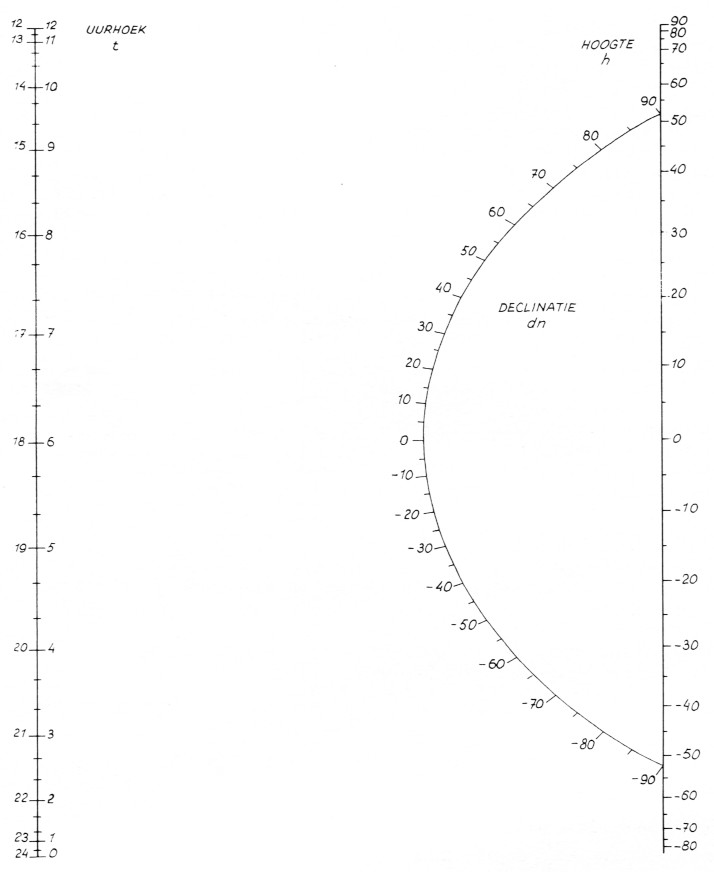
- Lees uit figuur 1 de hoogte "h" boven de horizon af.
- Lees uit figuur 2 het azimuth "A" af.
Verder uitgewerkt
1. De lokale sterretijd
Reken uw lengtegraad om in een tijdmaat. Dit is de lengtecorrectie, "LC". Vervolgens bepalen we de tijdcorrectie, "TC" = a × 10s. Rond rustig op gehele minuten af.
De sterretijd van Oh GMT op 00 OL lezen we af uit tabel 1: "T".
De lokale sterretijd is dan in formule: LST = T + LC + TC + a.
Voorbeeldje:
28 januari 21h GMT te Rotterdam, 52° NB en 4° 30' OL.
LC = 4.5° × 4m = 18m. TC = 21 × 10s = 210s = 4m.
LST = 8h 27m + 18m + 4m + 21h = 29h 49m = 5h 49m.
2. De rechte klimming
We interpoleren lineair in tabel 1 tussen dag "n" en "n+1". Dit is een aanname.
RKL = RK(n)+ -a [RK(n+1) - RK(n)].Voorbeeldje: 28 januari 21h GMT.
RKL = 7h 46m + 24 21 Oh 51m - 7h 46m) = 7h 46m + -7 (66m) = 711 46m + 581n = 8h 44m.3. De uurhoek van de maan, "t"
t = LST - RKL; eenvoudiger kan het niet.
Voorbeeldje: gegevens als boven. Omdat RKL groter dan LST is, mogen wij bij LST 24h bijtellen. t = 29h 49m - 8h 44m = 21h 05m.
4. De declinatie
Ook hier interpoleren we lineair in de tabel 1 tussen dag "n" en "n+1".
dn = D(n)+24 [D(n+1) - D(n)].Voorbeeldje: 28 januari 1983, 21h GMT.
dn = 23o 31 + 21 24 (200 491 - 230 31)= 230 31 - 8 - 7 (20 141)=230 31 -10 571= 210 61.5. De hoogte van de maan boven de horizon
In figuur 1 leggen we een denkbeeldige lijn tussen het punt t op de uurhoek-as (links) en dn op de gebogen declinatielijn en we snijden de hoogte-as in "h".
Als de hoogte negatief is, dan staat de maan onder de horizon.
Voorbeeld: De lijn door t = 21h 5m en dn = 21° snijdt de hoogte-as in h = 45°.
6. Het azimuth
In figuur 2 snijden we een denkbeeldige lijn door "dn" op de rechter as en "h" op de kromme hoogte-as met de linker as A. Het snijpunt "A" is de richting van de maan vanuit het noorden. Deze richting kan nog negatief (oostelijke hemeldeel) of positief (westelijke hemeldeel) zijn. Hiervoor bestaat een eenvoudig criterium.
Als t kleiner is dan 12u staat de maan westelijk, maar als t tussen 12h en 24h in ligt dan staat de maan oostelijk. Zoals we in figuur 2 kunnen zien, zijn de einden van de azimuth as nogal onnauwkeurig. Een klein foutje is zo gemaakt, met aanzienlijke afwijkingen als gevolg. Een formuletje schiet ons in zo'n geval to hulp:
sin A = [cos(dn) sin(t)] / cos(h). Bij de oplossing van deze vergelijking maken we toch handig gebruik van figuur 2. Veronderstel we vinden dat sin A = 0.07, dan vinden we als oplossing voor A ≈ 4°; echter 180° - 4° = 176° voldoet dan ook. Uit het geschatte snijpunt uit figuur 2 weten we of we 4° of 176° moeten kiezen.
Voorbeeldje: 28 januari om 21/1 GMT.De lijn door dn = 21° en h = 45° snijdt de A-as in figuur 2 bij ± 116°. De uurhoek is 21h 5m dus we moeten het minteken gebruiken: A = -116°; dit is tussen OZO en ZO. Met formules (zie appendix) hebben we kunnen berekenen dat h = 44.4° en A = -115.8°.
Nog een extra voorbeeld: 28 januari 1983, 23h 30m GMT.
- LST = 8h 27m + 18m + 4m + 2311 30m = 8h 19m
- RKL = 7h 46m + 5m = 8h 5m
- t = gh om _8h sim = 23h 28m
- dn = 230 31 - 20 111 = 200 521
- h = 600
- A = ?; het snijpunt ligt boven de A-as: omdat t < 24h verwachten we A - 180°.
De berekening met de sinusformule leert ons dat sin A - 0.26, dus A = -165°.
De berekening met de formules uit de appendix levert op h = 58.30 en A = -166.20.
Voor antennes met relatief kleine openingshoeken 50 bij -3B (30 dB "gain") is deze nauwkeurigheid nog voldoende.
Amateurs met niet eleveerbare antennes moeten testen of luisteren als de maan laag aan de horizon staat. Dit is kort na opkomst of voor ondergang. Het tijdstip van opkomst halen we uit de krant of agenda, of we kunnen het zelf bepalen. De beschreven berekening lijkt gecompliceerd, maar dat is slechts schijn. We moeten gewoon de voorafgaande berekening nu in omgekeerde volgorde uitvoeren.
Als de maan opkomt, heeft zijn middelpunt een hoogte 00. Lees af de rechte klimming en declinatie op dag "n", Oh GMT. Bepaal uit figuur 1 de bijpassende uurhoek "t". Voor opkomst moet deze liggen tussen ongeveer 15h en 21h, bij ondergang tussen 3h en 9h (uurhoek). De bijbehorende lokale sterretijd berekenen we uit: LST = t + RKL. Voor RKL nemen we de rechte klimming van Oh GMT. Van de lokale sterretijd trekken we de sterretijd T, zie tabel 1, de lengtecorrectie en de tijdcorrectie af. Het restant, "b" uur, is ongeveer het tijdstip van opkomst of ondergang van de maan, in GMT. Echter in die "b" uur is zowel de rechte klimming als de declinatie van de maan aanzienlijk veranderd. We gaan dus zowel de rechte klimming als de declinatie corrigeren en we herhalen de berekening met de rechte klimming en declinatie van "b" uur, i.p.v. Oh GMT. Zodoende vinden we dan "c" uur, een betere benadering. Een volgende correctie levert "d" enz. Na "c" uur kunnen we stoppen.
Het een en ander heb ik in tabelvorm (tabel 2) uitgevoerd voor maansopkomst op 28 januari 1983. Het azimuth A lezen we bij de declinatie van "b" uur af uit figuur 2. De derde keer is dus overbodig, de correctie is slechts 4m (A 10). We zien dat bij de tweede keer (uitgaande van 14h 41m) naast de rechte klimming ook de declinatie veranderd is, waardoor ook weer de uurhoek groter is geworden.
| 1e keer | 2e keer | 3e keer | |
|---|---|---|---|
| RKL | 7h 46m | 8h 26m | 8h 29m |
| do | 23° 3' | 21° 41' | 21° 35' |
| t | 15h 40m | 16h 00 | 16h 00m |
| LST | 23h 26m | 24h 28m | 24h 31m |
| TC | 0 | 2m | 3m |
| schatting | 14h 41m | 15h 43m | 15h 47m |
| GMT | "b" | "c" | "d" |
| T = 8h 27m LC = 18m | |||
De rechte klimming werd 40m groter, de uurhoek 20m, dus schatting "b" en "c" verschillen een uur, "c" en "d" slechts 4m. De door de astronomen opgegeven tijd van opkomst is 15h 57m GMT. Het verschil bedraagt 10m. De oorzaak van het verschil is de lineaire interpolatie, deze is onvoldoende. Ook hierin kan worden voorzien, maar dat zou het voorbeeld onnodig ingewikkeld gemaakt hebben.
Appendix
De gebruikte formules:
sin(h) = sin(NB) sin(dn) + cos(NB) cos(dn) cos(t).
sin(A) = [cos(dn) sin(t) / cos(h).
sin(dn) = sin(NB) sin(h) + cos(NB) cos(h) cos(A).
De laatste formule dient ter controle van de juiste waarde van het azimuth A.
PA0DAR.