Modulatie
In de zendamateurpraktijk wordt modulatie altijd toegepast. Een zo algemene signaalbewerking verdient een nadere beschouwing.
Modulatie als bewerking
Om met een zender een bepaalde informatieoverdracht te bereiken, moet de over te dragen informatie zodanig worden bewerkt, dat ze door de antenne kan worden uitgestraald. Deze bewerking wordt moduleren genoemd.
Moduleren komt meestal op het volgende neer: Men gaat uit van een sinusvormig signaal (oscillatorsignaal) waarvan of de frequentie, Of de fase, Of de amplitude wordt veranderd. Dit veranderen gebeurt door de over te dragen informatiestroom. Dus frequentie, fase of amplitude worden afhankelijk gemaakt van een stuursignaal, b.v. een versterkt mikrofoonsignaal.
Typen modulatie
Een sinusvormige spanning kan als volgt worden geschreven:
Uo = A. sin (ωct + Φ)
Hierin is:
Uo de beschreven spanning
A de amplitude
ωc de (radiaal) frequentie
Φ de fase
De bewerking modulatie kan nu worden toegepast op een van de konstanten, dus op de amplitude, frequentie of de fase. Men spreekt dan ook van amplitude, frequentie of fasemodulatie.
Behalve de bovenbeschreven opvatting van modulatie is het ook mogelijk om op andere wijze te moduleren. Voorgaande leidt tot de zgn. frequentie multiplex modulatie. Dat wil zeggen, dat er naar het beschikbare frequentiespektrum wordt gekeken en dat dit zo efficient mogelijk wordt gebruikt voor massatransport van informatie.
Een ander uitgangspunt is te kijken naar de beschikbare tijd en aan iedere informatiedrager een klein beetje tijd te geven om die informatie over te dragen. Dit is de zgn. tijd multiplex modulatie. Deze laatste manier van moduleren blijft in dit artikel buiten beschouwing. Overigens dient wel te worden opgemerkt, dat deze "TDM" de frequentie multiplex modulatie geheel zal overschaduwen.
AM, SSB, FM en PM
Zoals al opgemerkt, kan van een oscillatorsignaal de amplitude, de frequentie of de fase worden gemoduleerd (veranderd). Er ontstaat dan resp. AM (SSB), FM of PM. De eigenschappen van het gemoduleerde signaal (verder "modulaat" te noemen) verschillen sterk, afhankelijk van het feit, of de amplitude dan wel de frequentie(fase) wordt beihvloed. Om het proces AMmodulatie te illustreren wordt vaak een tijd-spanningsgrafiek getekend. Bij FM (PM) is een frequentie-vermogens grafiek zinvol.
AM en SSB
De diverse amateur-handboeken behandelen AM doorgaans uitvoerig. SSB komt er meestal wat magerder af, terwlil AM in de amateurpraktijk een ondergeschikte rol speelt. Vatten we AM hier nog even kort samen:
Bij AM is er een draaggolf, die altijd onveranderd blijft. Tevens zijn er twee zijbanden, een met een frequentie lager dan de draaggolf (lage zijband) en een met een frequentie hoger dan de draaggolf (hoge zijband). Beide zijbanden zijn elkaars spiegelbeeld, met de draaggolf als spiegel. Grafisch ziet e.e.a. er als volgt uit (zie figuur 1).
Fig. 1.
Door nu met filters of andere trucs de draaggolf en een zijband te verwijderen, ontstaat het SSB signaal. Men kan naar smaak de hoge (USB) of de lage (LSB) zijband uitzenden. Er ontstaat dan een signaal volgens figuur 2.
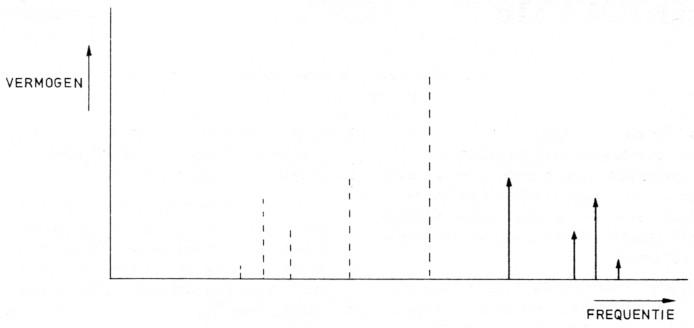
Fig. 2.
FM en PM
De opbouw van een FM (en PM) spektrum is heel wat gekompliceerder dan dat van een AM of SSB spektrum. Het spektrum is nl. van een aantal faktoren afhankelijk. Om iets over een dergelijk spektrum te kunnen zeggen, moeten er eerst een paar begrippen worden vastgelegd:
ZWAAI: Het verschil tussen de hoogste frequentie van de draaggolf en de laagste noemt men de zwaai. Bij 2 meter FM zenders is de zwaai meestal 3 à 5 kHz.
MODULATIE-INDEX: De modulatie-index is gedefinieerd als de zwaai, gedeeld door de hoogste modulatie-frequentie, dus:
Waarbij:
Δf = zwaai
fm = hoogste modulatiefrequentie
Wanneer het over te dragen signaal bestaat uit spraak, kunnen we voor fm = 3 kHz nemen. Voor 2 meter FM wordt de modulatie-index dan:
dus M ligt voor de 2 meter FM zenders meestal tussen de 1 en 2.
In het gebied tussen de 88 en 104 opererende omroepzenders is de modulatie-index veel groter
voor mono bedrijf.
Het FM (of PM) spektrum kan nu worden bepaald, wanneer of de modulatie-index van de modulator en de hoogste modulerende frequentie bekend is, of de zwaai en de hoogste modulerende frequentie.
Laten we eens aannemen, dat een 2 meterzender een modulatie-index heeft van 1 en gemoduleerd wordt met een sinus van 3 kHz (zie figuur 3).
Fig. 3.
Meteen valt op, dat de frequentie-afstand tussen de zijbanden 3 kHz = de modulatiefrequentie is. Dit is altijd het geval. De frequentie-afstand tussen de zijbanden bij een FM of PM modulaat is gelijk aan de frequentie van het modulerende signaal. Tevens valt de symmetrie op. Ook dit is een eigenschap die bij FM en PM (en AM!) thuishoort. Verder is er een groot aantal zijbanden zichtbaar, terwijl er met een sinus werd gemoduleerd. Dit is een typisch verschil tussen FM en PM enerzijds en AM en SSB anderzijds. Ook als alle onderdelen van een FM zender ideaal zouden zijn, dan zou toch het spektrum een groot aantal zijbanden vertonen.
Bessel funkties
De amplitude van deze zijbanden t.o.v. de draaggolf is wiskundig vastgelegd door Bessel, in de naar hem genoemde uitdrukkingen.
Om niet in de wiskunde verzeild to raken, maakt men gebruik van tabellen en grafieken.
FM en PM zijn tot nu toe steeds als gelijk behandeld. Het verschil wordt pas duidelijk wanneer aan de modulator niet een maar meer frequenties worden toegevoerd. Verdubbelt men bij een FM zender de modulerende frequentie, dan halveert de modulatie-index. Bij PM blijft deze echter gelijk. Vandaar, dat een PM-zender beluisterd met een FM ontvanger meestal schel aandoet (b.v. oudere mobilofoons). Zolang er echter sprake is van een modulerende frequentie, is aan het spektrum niet te zien, of er sprake is van een FM of PM gemoduleerde zender.
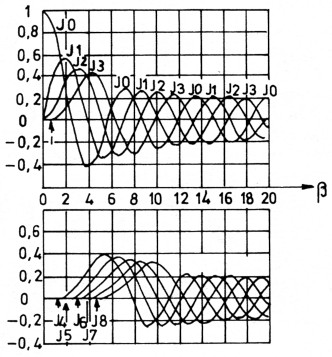
Β = modulatie-index
J0 = draaggolfniveau
J1 = niveau eerste paar zijbanden
J2 = niveau tweede paar zijbanden
J3 = niveau drede paar zijbanden
enz.
Om het spektrum van de FM of PM zender te kunnen tekenen, nu eerst wat Bessel funkties in tabel- en grafiekvorm.
| n | Jn(0.2) | Jn(0.4) | Jn(0.6) | Jn(0.8) | Jn(1.0) | Jn(1.25) | Jn(1.5) | Jn(1.75) | Jn(2.0) | Jn(2.5) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | +0,9900 | +0,9604 | +0,9120 | +0,8463 | +0,7652 | +0,6459 | +0,5118 | +0,3690 | +0,2239 | -0,0484 |
| 1 | +0,0995 | +0,1960 | +0,2867 | +0,3688 | +0,4401 | +0,5106 | +0,5579 | +0,5802 | +0,5767 | +0,4971 |
| 2 | +0,0050 | +0,0197 | +0,0437 | +0,0758 | +0,1149 | +0,1711 | +0,2321 | +0,2940 | +0,3528 | +0,4461 |
| 3 | +0,0002 | +0,0013 | +0,0044 | +0,0102 | +0,0196 | +0,0369 | +0,0610 | +0,0918 | +0,1289 | +0,2166 |
| 4 | +0,0003 | +0,0010 | +0,0025 | +0,0059 | +0,0118 | +0,0209 | +0,0340 | +0,0738 | ||
| 5 | +0,0002 | +0,0007 | +0,0018 | +0,0038 | +0,0070 | +0,0195 | ||||
| 6 | +0,0002 | +0,0006 | +0,0012 | +0,0042 | ||||||
| 7 | +0,0001 | +0,0002 | +0,0008 | |||||||
| 8 | +0,0001 |
n = nummer van de zijband, tussen haakjes staat de modulatie-index.
De grafiek geeft de amplitudes van de zijbanden aan t.o.v. de amplitude van de draaggolf. Hierbij is J0 de draaggolfamplitude, J1 de eerste zijband, J2 de tweede, enz.
Β geeft de modulatie-index aan.
In de tabel staat vertikaal het nummer van de zijband aangegeven en horizontaal de modulatie-index. Kiest men nu opnieuw het voorbeeld van de 2 meter FM zender, gemoduleerd met 3 kHz en een zwaai van 3 kHz, dan volgt uit de tabel: (M = 1)
| draaggolf amplitude | (J0)= + 0,7652 |
|---|---|
| 1e zijband | (J1)= + 0,4401 |
| 2e zijband | (J2)= + 0,1149 |
| 3e zijband | (J3)= + 0,0196 |
| 4e zijband | (J4)= + 0,0025 |
| 5e zijband | (J5)= + 0,0002 |
Met deze gegevens is nu het spektrum te konstrueren, door de amplitudes om te rekenen naar vermogens en in dBc uit te drukken.
Dit kan door de amplitude te kwadrateren, zodat een vermogen ontstaat en hiervan de 10log te nemen. Hetzelfde resultant geeft 20log van de amplitude te nemen.
b.v.: 3e zijband bij M = 1 is 0,0196
10log (0,0196)2 =
20log 0,0196 = -34,2dBc
Op de -74dBc punten is dit signaal nog altijd 30 kHz breed. Het is nu duidelijk, waarom bij 25 kHz-raster er een modulatieindex van ten hoogste 1 kan worden toegepast.
Bij een 12,5 kHz-raster moet de modulatieindex worden verkleind. Op de +6 en -6 kHz punten bevat het spektrum van figuur 4 nog komponenten van -18.8dBc. Een ontoelaatbare storing in het nevenkanaal bij een dergelijk raster.
Frequentievermenigvuldiging
Eenvoudig is na te gaan, wat er met de modulatie-index van een FM modulaat gebeurt, wanneer de frequentie verveelvoudigt, d.m.v. een in klasse C ingestelde versterker. De modulerende frequentie blijft gelijk, echter de zwaai verveelvoudigt.
Als voorbeeld kan een frequentieverdubbelaar dienen. De zwaai verdubbelt dan. De modulatie-index echter ook. Immers, de modulatie-index is 
dus rechtevenredig met de zwaai. Een frequentievermenigvuldiging met een faktor n geeft dus een toename van modulatie-index van eveneens n maal. Op grond van de nieuwe modulatieindex kan dan het nieuwe spektrum, dus na de vermenigvuldiger worden berekend. Het is dus niet zo, dat een FM of PM signaal via frequentievermenigvuldiging eenvoudig n maal zo breed wordt.
Verdubbelen we het in figuur 4 geschetste signaal, dan wordt de modulatie-index 2 en uit de tabel vinden we, dat voor Jn (2) = 0,0002 we de 7e zijband moeten hebben. De totale bandbreedte voor -74dBc is dan 2 × 7 × 3= 42 kHz, terwijl in figuur 4 de bandbreedte bij -74dB 30 kHz is. Een heel wat ander resultaat dan te veronderstellen, dat verdubbeling van figuur 4 een twee maal zo breed spektrum, dus 60 kHz, oplevert.
Fig. 4.
Bij frequentieverveelvoudiging van een FM of PM modulaat dient dus altijd het nieuw gevormde spektrum te worden bepaald via de modulatie-index en de Bessel funkties.
Andere vormen van FM en PM
Naast het met een sinus gemoduleerde FM of PM signaal uit het voorgaande gedeelte zijn er nog andere vormen van FM en PM in gebruik bij zendamateurs. Te denken valt aan FSK (frequency shift keying), telex, slow scan tv e.d.
Voor al deze FM of PM-achtige modulatie vormen kan op dezelfde manier, zoals hierboven aangegeven, het spektrum worden voorspeld.
Bij de bepaling van een FSK spektrum bijvoorbeeld, of telex, dient men er wel rekening mee te houden, dat het signaal dat de frequentieomschakeling verzorgt liefst geen blok is. Een blokvormig signaal zorgt voor een zeer breed spektrum.
Voor een ingewikkeld signaal, zoals een min of meer gefilterde blokspanning, kan het beste de harmonischen inhoud worden geschat en vervolgens via de modulatieindex het uiteindelijke spektrum worden samengesteld. Het geheel analytisch opsporen van een dergelijk signaal is veel te tijdrovend.
Literatuur
- Betts, J.A. Signal Processing, modulation and noise. Londen: Hodder and Stoughton, Unibooksseries, z.j.
- Manassewitsch, V. Frequency synthesizers. New York: Wiley & Sons, 1980.
PA0WOW.