Strip-line techniek
Een variant ter realisering van amateurprojekten in het VHF/UHF bereik.
Het is niet voor niets dat men vroeger de UHF-banden de loodgietersbanden noemde. Zenders en ontvangers voor deze banden bestonden voornamelijk uit strip-lines, leggers en aanverwante koperstrippen. Het enige verschil met de echte loodgieter was de manier van werken. De loodgieter keek niet op een mm, terwijl de zenderbouwer rekening hield met elke mm afwijking. Tegenwoordig is hier heel wat veranderd. Met de opkomst van de printplaat gaat het maken van een afgestemde kring veel gemakkelijker. Het is voldoende om een keer de kring te berekenen en dan in de vorm van een strip-line op een printfilm te zetten. Het fotografische printenprocede doet de rest.
In dit artikel hoop ik uiteen te zetten wat een strip-line is, hoe deze ontstaat en enkele berekeningen, grafieken en toepassingen geven zodat u wat meer inzicht krijgt in zo'n strip-line of om eventueel zelf zoiets te maken.
Strip-lines zijn ontstaan omdat de spoelen in het UHF gebied zo klein worden, dat ze bijna niet te maken zijn. Een recht stuk draad heeft al voldoende zelfinduktie waardoor het wikkelen niet meer nodig is. Een strip-line bestaat in zijn eenvoudigste vorm uit een vlakke geleider (de strip-line) op een dunne draagplaat waarvan de rugzijde geheel gemetalliseerd is (zie figuur 1). Men kan de strip-line als een opengeklapte coaxkabel beschouwen. Er zijn diverse vormen van strip-lines. De voornaamste zijn de onsymmetrisch (zie figuur 2) en de micro-slotgeleiding (zie figuur 3). Beide uitvoeringen noemt men micro-strips. De isolatie tussen afgestemde strip-line en het massavlak is het printmateriaal. Dit heeft een bepaalde dikte die weliswaar voldoende isoleert maar toch nog zorgt voor een kapaciteit tussen strip-line en massa. Wanneer een kant van de strip-line aan massa ligt hebben we al een afgestemde kring waarvan de L gevormd wordt door de lengte van de line.
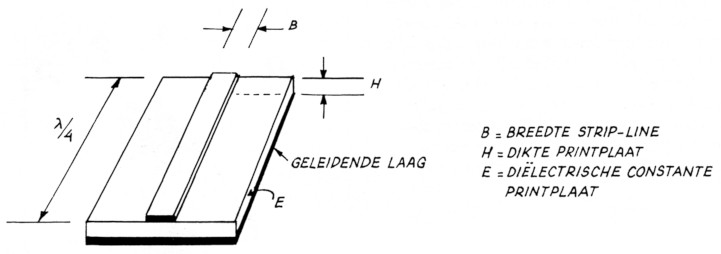
Fig. 1. Een ¼λ resonatiekring in strip-line.
Fig. 2. Onsymetrisch.
Fig. 3. Micro-slotgeleiding.
Elke strip-line is in wezen een ¼λ of een ½λ lang. Wanner we echter de lengte opmeten van diverse strip-lines dan is de lengte altijd korter. Dit korter zijn dan de verwachte lengte ontstaat door de kapaciteit. Hoe groter de C is hoe korter de strip-line. Vaak is de lengte dan nog te lang. Vandaar dat men aan de top een kondensator plaatst waardoor de line nog korter kan zijn.
Voor de amateur is de onsymmetrische strip-line het ideaalste, daar deze naar een twee-dimensionale opbouw teruggevoerd kan worden: lengte × breedte. We zullen deze strip-line dan ook nader gaan bekijken. Indien men een onsymmetrische strip-line voor b.v. een kring wil opbouwen dan kan men deze zowel als ¼λ-line uitvoeren maar ook als ½λ-line. Bij de volgende beschouwing zullen we alleen de ¼λ bezien daar deze het eenvoudigst te maken is (zie figuur 2). Het te bereiken ideaal, laten we dit de Q-faktor noemen, hangt voornamelijk of van:
- het printmateriaal en inherent hieraan de ε van het materiaal
- de dikte van de print h
- de strip-line breedte b
Bij normaal print bereikt men bij een dikte van 1,5 mm al gauw een Q-waarde van 300, hetgeen dus zeer goed is.
Een zeer belangrijke faktor is de impedantie Z. Deze laat zich berekenen uit:
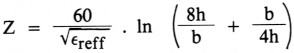
Voor b < h.
In deze formule is In de natuurlijke logarithme met het grondtal e = 2,718. εreff is de werkzame dielektrische konstante van de print.
Om met deze formule te kunnen werken moet men eerst εreff berekenen. Deze volgt uit de volgende formule:
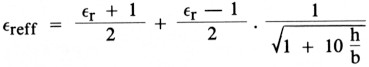
In deze formule wordt εr gebruikt. Dit is de relatieve dielektrische konstante van het materiaal.
Enkele waarden van εr zijn:
CEVAUSIT 4,8 (fabrieksnaam)
TEFLON/FIBERGLAS 2,55
DUROIT 2,3 (fabrieksnaam)
BERYLLIUMOXIDE 6,8
ALUMINIUMOXIDE 10,0
LUCHT 1,0
Met deze kennis kan men de volgende vergelijking gebruiken om de kapaciteit te berekenen:
Waarin:
ω de cirkelfrequentie (2πf)
Z de impedantie
Leff de 'echte' strip-line lengte
λl de golflengte op de print
Denk erom dat 2πLeff/λl in radialen staat.
Hierbij moet opgemerkt worden dat de λ op de print anders is dan we normaal zouden verwachten. We zijn gewend om de golflengte te berekenen, uitgaande van de lichtsnelheid 300.000 km/s. Voor radiogolven geldt ook deze snelheid, maar alleen in de lucht. In een andere stof is de voortplantingssnelheid lager waardoor λ dus ook lager wordt. Bij coaxkabel zijn we gewend om hiermee te werken. Denk maar aan de verkortingsfaktor. Eenzelfde faktor geldt ook voor printmateriaal. We moeten dus λ voor het printmateriaal gaan berekenen. Hiervoor gebruiken we de volgende formule:
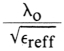
waarin λo de golflengte in de lucht is.
In deze formule is een deel van de Q-faktor van het printmateriaal meegenomen. Met deze gegevens is het mogelijk om ¼λ-striplines te berekenen.
Ook kan men de induktie en kapaciteit berekenen. Voor de induktie geldt:
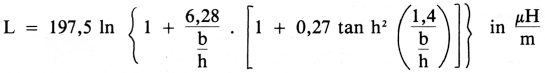
Voor de kapaciteiten geldt:
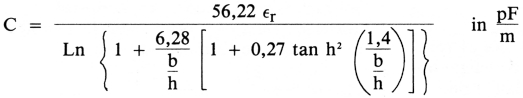
Ook hier weer staat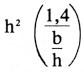 
in radialen (1 radiaal = 57,3°, immers 2πR = 360°).
Van droge theorie naar de praktijk
Zo, dat waren dan een heleboel formules. Hopelijk heeft u zich er door kunnen worstelen. Velen van u zullen nu denken: `kan dat niet eenvoudiger'. Ja zeker kan dat. We hebben immers de computer. Men heeft met de computer allerlei variaties berekend en deze in een diagram verzameld. Het is duidelijk dat bij een bepaalde printdikte vele strip-line-breedtes kunnen passen. Men moet bij dergelijke berekeningen van parameters gebruik maken, dat wil zeggen vaste gegevens. Men ziet dan wel wat er uit rolt.
Een voorbeeld:
Voor een ¼λ-strip-line gebruiken we de volgende gegevens:
εr diëlektrische konstante van de print
h dikte van de print
f de frequentie
C de kringkapaciteit
Uit deze gegevens zijn nu de karakteristieken van figuur 4 berekend.
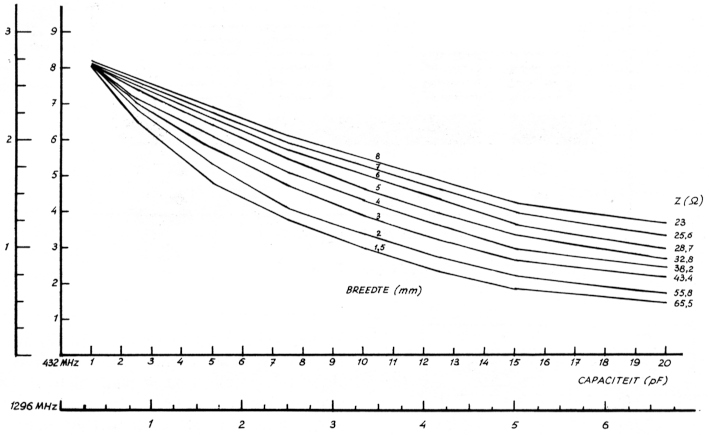
Fig. 4. Grafiek voor het bepalen van strip-lines.
Met deze grafieken zijn we in staat om voor diverse printdiktes de lengte van de line en de grootte van de top-kapaciteit te halen.
Het berekenen van een strip-line
Hoe gaan we nu te werk. Aan de hand van een voorbeeld zullen we dit laten zien. We willen voor een zender op 432 MHz een strip-line maken. We kiezen als breedte 2 mm en als printdikte 1,5 mm. Uit de grafiek van figuur 4 kunnen we nu aflezen dat de lengte van de strip-line 3,8 cm moet zijn wanneer de kapaciteit 9 pF is.
Tevens kunnen we zien dat de impedantie z = 55,8 Ω is.
Een tweede voorbeeld: frequentie is 1296 MHz, b is 5 mm, C is 2 pF. Uit de grafiek kunnen we nu halen dat de lengte 2 cm moet zijn.
Vaak wordt de kondensator als variabele C uitgevoerd. Hierdoor is de kring afstembaar geworden. Een mooi voorbeeld hiervan is de universeel bruikbare konverter uit CQ-PA nr. 18. Bekijken we de print op blz. 481 dan kunnen we opmeten dat de lengte van de strip-lines L8 en L9 3,5 cm is. De breedte van de lines is 4 mm. Uit figuur 4 kunnen we dan aflezen dat voor een printdikte van 1,5 mm de kapaciteit 8 pF moet zijn. Kijken we in de komponentenlijst op blz. 484 dan zien we dat voor C1 en C2 kondensatoren van 2 tot 10 pF gebruikt worden. Dit komt dus overeen met de waarde uit figuur 4.
Low-pass-filter voor 2 m
Om het nu niet alleen bij droge theorie to laten, nog een praktisch voorbeeld als slot. In figuur 5 zien we een low-pass-filter voor twee meter met strip-lines. Het kan onder andere gebruikt worden in kombinatie met de al genoemde universeel bruikbare konverter en een twee-meter-ontvanger wanneer u de konverter voor telefonie wilt gebruiken. Wat eigenschappen van het filter:
kantelfrequentie = 150 MHz
doorlaatdemping 0,1 - 0,2 dB
sperdemping > 60 dB
afsluitimpedantie 60 Ω
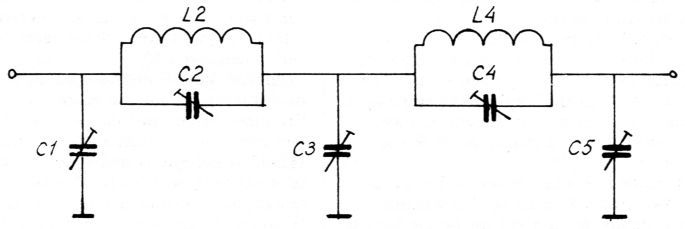
Fig. 5a. Filter voor 2 meter.
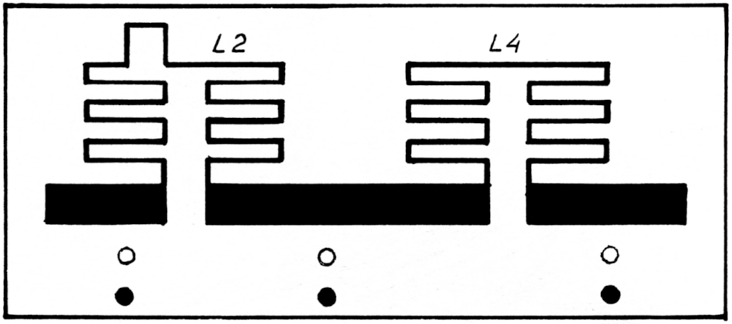
Fig. 5b. Print van het filter.
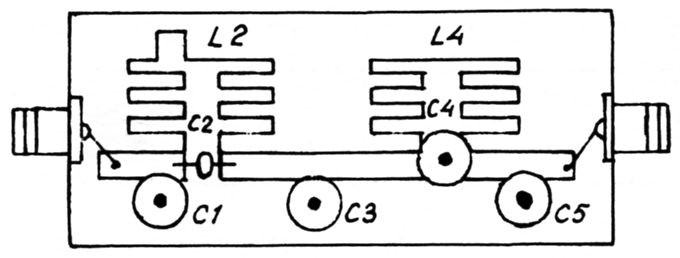
Fig. 5c. Componentenopstelling.
Het filter wordt gemaakt op een stukje dubbelzijdige printplaat. De kondensatoren zijn deels vaste en deels variabele.
Volgens berekeningen moeten de kondensatoren de volgende waarden hebben:
C1 = 22 pF
C2 = 1,3 pF
C3 = 34,4 pF
C4 = 3,6 pF
C5 = 19,8 pF
U ziet wel dat het merendeel als trimmer uitgevoerd moet worden. De opgegeven doorlaatdemping kon ik niet halen. Bij mij was de demping ongeveer 0,8 dB, maar in vergelij king met een filter met gewone spoelen was er geen verschil meetbaar.
Ik hoop dat ik iets over strip-lines uit de doeken gedaan heb. Het is weer eens iets anders.
Literatuur
- QST
- Funkamateur
- ARRL handboek 1983
- RSGB handboek
A.W. de Herder, PE1KEY.