Theoretische beschouwingen over de SWR-meter
1. Inleiding
De juiste werking van de SWR-meetbrug is voor vele amateurs een raadsel. Het meetprincipe is vrij eenvoudig, doch nogal verwarrend. Ook gaat men er in vele handboeken nogal snel overheen. Omdat de werking van dit toestel mij reeds lange tijd interesseerde ben ik er een studie over begonnen. Het meetprincipe had ik vrij snel achterhaald, doch wat men eigenlijk meet, namelijk de staande golf verhouding zelf, dat is een ander paar mouwen. Voor ik de cijfervoorbeelden als afsluiting van dit artikel op papier zette, heb ik eerst de zware materie van de transmisielijnen moeten doorworstelen. Eenmaal inzicht hierin komt men terecht in een fascinerende wereld die de moeite van het ontdekken waard is.
2. Hoe wordt de SWR gemeten?
De SWR of Standing Waves Ratio (verhouding tussen staande golven) wordt gemeten met een reflektometer. Ook komt men in de literatuur de naam richtkoppler tegen. Figuur 1 geeft het principeschema van zo'n reflektometer. S = afscherming / AG = antennegeleider / MG = meetgeleider.
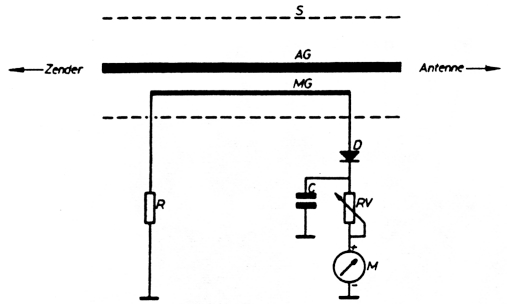
Fig. 1.
AG vormt samen met S een coaxiale configuratie, welke dezelfde impedantie heeft als de antennevoedingskabel. MG is een parallelgeleider van AG en wordt gebruikt om te meten. Weerstand R sluit de meetgeleider of naar massa. Diode D en kondensator C vormen een topgelijkrichterschakeling, terwijl met de regelbare weerstand RV de gevoeligheid van meter M kan ingesteld worden.
3. Hoe werkt de reflektometer?
Als we KG opnemen in een coaxkabel waarlangs we energie naar een antenne sturen, dan zal in MG een spanning opgewekt worden, welke gelijkgericht wordt door diode D en afgevlakt wordt door kondensator C. De ontstane gelijkspanning zal door meter M een gelijkstroom sturen welke op haar beurt de naald van de meter zal laten uitslaan.
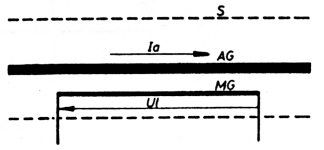
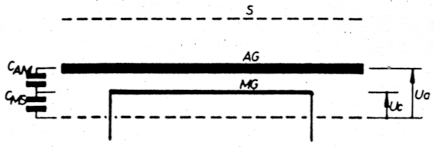
3.1. De kapacitieve spanningsdeler
AG vormt samen met MG een kapaciteit CAM, terwijl MG samen met S de kapaciteit CMS vormt. Beide kapaciteiten vormen een kapacitieve spanningsdeler. De spanning tussen MG en S kan met onderstaande formule berekend worden:
Vc = CMS : CMS + CAM
3.2. De geinduceerde spanning
Ten gevolge van de antennestroom Ia door AG zal in de nabijgelegen geleider MG een spanning Ul geinduceerd worden. De kombinatie AG/MG vormt dus een stroomtransformator.
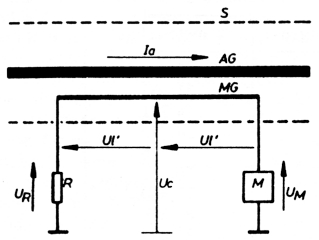
3.3. Samenspel van Uc en Ul
De spanning Ul staat symmetrisch ten opzichte van het middelpunt van MG. We kunnen stellen dat ten opzichte van dit middelpunt zich twee deelspanningen Ul' bevinden, waarbij geldt Ul' = Ul/2. Het middelpunt van MG bevindt zich op het potentiaal Uc. Over weerstand R komt nu de spanning UR te staan.
UR = Uc + Ul'.
Over het meetcircuit komt nu de spanning UM te staan.
UM = Uc - Ul'.
Het equivalent schema van figuur 5 geeft hier meer duidelijkheid over.
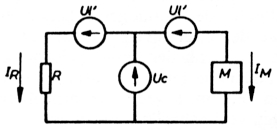
Fig. 5.
De hoger vermelde formules kan men vinden door de wetten van Kirchhoff en de theorie van de mazennetwerken toe te passen.
4. De optimale reflektometer
Als we de reflektometer nu zodanig konstrueren dat:
- zijn karakteristieke impedantie gelijk is aan die van de gebruikte zender en de antenne-voedingskabel;
- bij een zuivere Ohmse afsluiting van de uitgang, gelijk aan de karakteristieke impedantie van de zender, de spanningen Uc = UP , dan zal de meterspanning UM = 0 Volt bedragen, zal er geen stroom IM vloeien en zal de naald 0% aanduiden.
Nemen we deze reflektometer op in de antenneleiding, dan zal bij optimale aanpassing van de antenne aan de zender de meternaald eveneens 0% aanduiden. Bij misaanpassing zal Uc = Ul' en zal de meternaald een bepaalde uitwijking vertonen. Hoe groot de misaanpassing nu is, wel, daar hebben we het raden naar, voorlopig althans.
5. Wat gebeurt er als we R en M van plaats verwisselen?
Aan de waarden van de spanningen Uc, Ul en Ul' verandert er nets omdat we geen veranderingen aangebracht hebben aan de spanningsbepalende komponenten van de geoptimaliseerde reflektometer. Enkel UR en UM zullen een andere waarde hebben als voorheen, omdat we beide komponenten van plaats verwisseld hebben. Over M staat nu de som van Uc en Ul', zodat:
UM = Uc + Ul'.
Over R staat nu het verschil van Uc en Ul, zodat:
UR = Uc - Ul'.
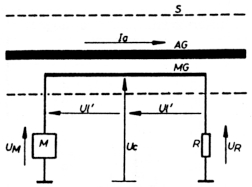
Fig. 6.
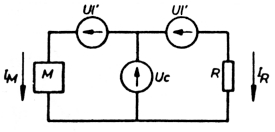
Fig. 7.
5.1. De reflektometer gebruikt als vermogenindikator
Sturen we nu een optimaal aangepaste antenne via de, zoals in figuur 4 geschakelde, reflektometer, dan zal UR = 0 volt en UM = 2 × Uc zijn. UM zal een meterstroom IM veroorzaken welke op zijn beurt de naald van de meter zal laten uitslaan. Omdat UM = fie (Uc), Uc = fie (Ua) en Pa = fie (Ua) zal UM = fie (Pa). Met andere woorden, de uitslag van de meternaald is een funktie (fie) van het door de antenne gekonsumeerde vermogen. Indien we nu de meter voorzien van een (kwadratische) vermogenschaal dan kunnen we rechtstreeks het vermogen aflezen, wat zeker zijn nut zal hebben.
Merk op dat bij misaanpassing van de antenne de meteruitslag niet meer overeenstemt met het door de antenne opgenomen vermogen daar nu UM = fie (Uc, Ul' ) en Ul' ≠ fie (Ua).
5.2. De powerschaal
| % meterschaal | % vermogen | % vermogen | % meterschaal |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 10 | 1 | 10 | 31,663 |
| 20 | 4 | 20 | 44,721 |
| 30 | 9 | 30 | 54,772 |
| 40 | 16 | 40 | 63,246 |
| 50 | 25 | 50 | 70,711 |
| 60 | 36 | 60 | 77,460 |
| 70 | 49 | 70 | 83,666 |
| 80 | 64 | 80 | 89,443 |
| 90 | 81 | 90 | 94,868 |
| 100 | 100 | 100 | 100 |
De waarden in bovenstaande tabel kunnen berekend worden met onderstaande formules:
%P = (%M:10)2
%M =√%P × 10
%P = procent vermogenschaal
%M = procent meterschaal
6. Het bepalen van de SWR met de power-meters
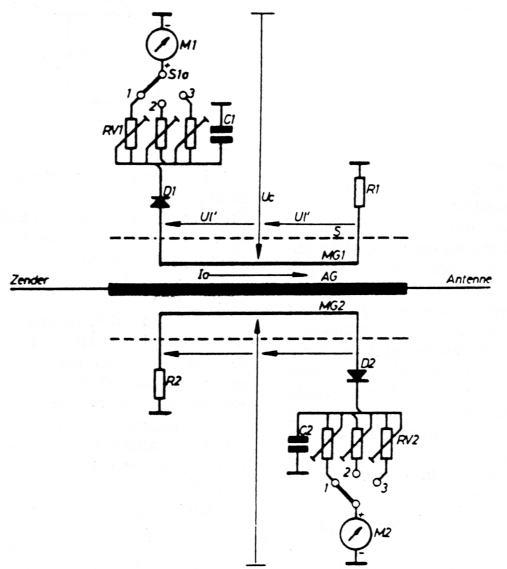
Fig. 8.
We kunnen met de reflektometer van twee zaken een indikatie geven:
- De mate van aanpassing: geen indikatie = juiste aanpassing / wel indikatie = misaanpassing.
- Het vermogen, verbruikt voor de antenne (enkel juist bij juiste aanpassing).
Indien we van beide indikaties gelijktijdig gebruik maken dan kunnen we en de SWR bepalen en bij misaanpassing het door de antenne opgenomen vermogen bepalen. Om een gelijktijdige meting van het 'voorwaarts-' en 'gereflekteerde-' vermogen to bekomen moeten we de reflektometer dubbel uitvoeren. Beide meeteenheden moeten identiek zijn, daar anders de gebruikte formules niet meer gelden. Figuur 8 geeft het principeschema van een veel gebruikte powermeter.
De meetkring rond M1 is identiek aan die rond M2, enkel de plaats van de afsluitweerstand R en het meetinstrument M zijn onderling verwisseld. De voorschakelweerstanden RV1 en RV2 zijn drie maal uitgevoerd en omschakelbaar d.m.v. een schakelaar S1. De voorschakelweerstanden zijn zodanig ingesteld dat bij elke stand van S1, 100% van de schaal overeenkomt met een ronde waarde voor het vermogen, namelijk in ons voorbeeld: 2 Watt, 20 Watt en 200 Watt.
Beide meters zijn voorzien van een (kwadratische) vermogenschaal, de aflezing van M1 noemt men 'FORWARD POWER', die van M2 'RFLECTED POWER'. Soms hebben beide instrumenten ook nog een lineaire schaalverdeling.
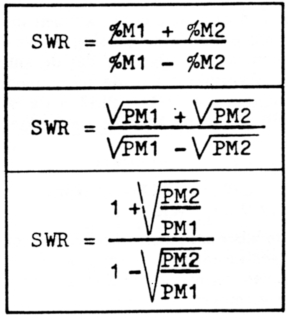
Als we de aflezing van M1 en M2 respektievelijk % M1 en % M2 noemen voor de lineaire schaalverdeling en PMI en PM2 voor de vermogens-schaalverdeling, dan kunnen we de SWR bepalen met een der nevenstaande formules.
Het aan de antenne afgeleverde vermogen kan met onderstaande formule berekend worden:
Pa = PM1 - PM2.
6.1. Voorbeelden
Van M1 leest men het vermogen af dat de zender aan de antenne zou kunnen leveren als er een optimale aanpassing is. Van M2 leest men het vermogen af dat de antenne minder verbruikt t.g.v. de misaanpassing. Het resultaat van PM1 - PM2 = Pa, of het werkelijke door de antenne verbruikte vermogen.
Voorbeeld 1
PM1 = 72 Watt, PM2 = 0 Watt, Pa = 72 Watt, SWR = 1.
Door de juiste aanpassing zal het door de antenne gekonsumeerde vermogen 100% bedragen van het maximum door de zender te leveren vermogen.
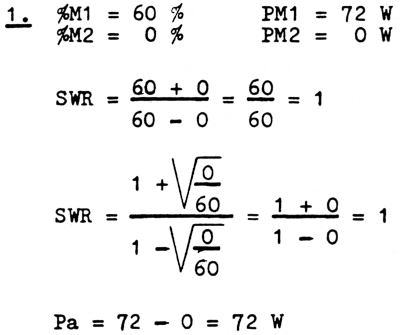
Voorbeeld 2
PM1 = 20 Watt, PM2 = 5 Watt, Pa = 15 Watt, SWR = 3.
Door de misaanpassing kan men slechts 75 % van het maximum aan vermogen benutten, wat een verspilling van 25 % betekent, wat toch al een serieuze waarde is.
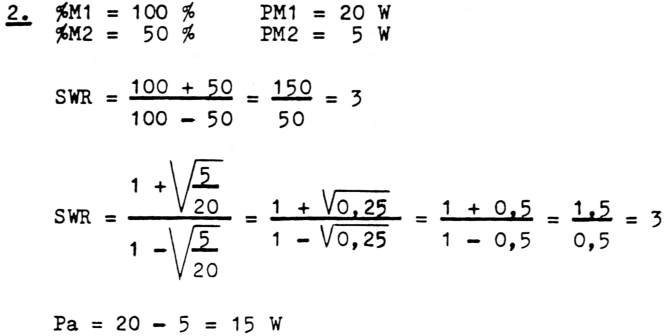
7. De SWR-meter met de SWR-schaal
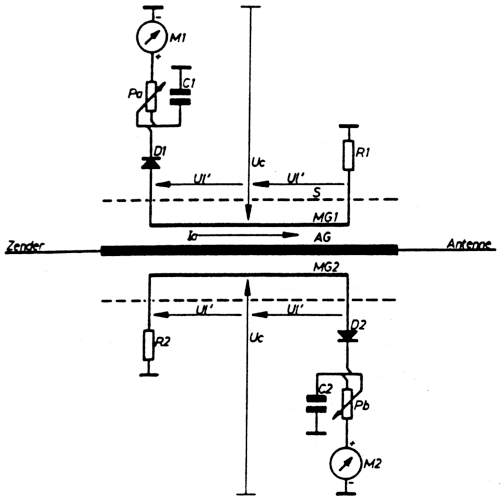
Fig. 9.
De hierboven besproken methode heeft als grote voordeel dat we een direkt beeld hebben van het door de antenne verbruikte vermogen. Het grote nadeel is dat het bepalen van de SWR nogal omslachtig is. Met onderstaande schakeling wordt het rekenwerk vervangen door het draaien aan het potentiometer.
RV1 en RV2 worden elk vervangen door een sektie van een tandempotentiometer, respektievelijk Pa en Pb. Met potentiometer P kan men nu kontinue de gevoeligheid van beide meters, M1 en M2, in gelijke mate veranderen.
7.1. Meetprocedure
De meters worden door middel van P1 in hun meest ongevoelige stand gebracht, de gehele weerstandswaarde van de potmetersekties staat in serie met de respektievelijke meter. De zender wordt ingeschakeld. Met potmeter P regelt men nu zodanig dat de naald van M1 juist 100% schaal aanduidt. De SWR kan nu berekend worden met de aangepaste formule:
SWR = 100 + %M2 : 100 - %M2.
Het is nu niet de bedoeling om de SWR te berekenen, doch wel om M2 van een SWRschaal te voorzien, zodat we direkt de waarde van de staandegolfverhouding kunnen aflezen. Dit kan omdat % M1 een konstante geworden is (% M1 is steeds 100%).
7.2. De SWR-schaal
De SWR-schaal kan samengesteld worden gebruikmakend van onderstaande formule, welke afgeleid is uit onderstaande formule:
%M2 = (100 × SWR) - 100: 1 + SWR.
Onderstaande tabel geeft %M2 i.p.v. SWR.
| SWR | % M2 | SWR | % M2 |
|---|---|---|---|
| 1,0 | 0,000 | 2,1 | 35,484 |
| 1,1 | 4,762 | 2,2 | 37,500 |
| 1,2 | 9,091 | 2,3 | 39,394 |
| 1,3 | 13,043 | 2,4 | 41,176 |
| 1,4 | 16,667 | 2,5 | 42,857 |
| 1,5 | 20,000 | 2,6 | 44,444 |
| 1,6 | 23,077 | 2,7 | 45,946 |
| 1,7 | 25,926 | 2,8 | 47,368 |
| 1,8 | 28,571 | 2,9 | 48,718 |
| 1,9 | 31,034 | 3,0 | 50,000 |
| 2,0 | 33,333 | 100,000 |
Merk op dat de SWR-schaal enkel bruikbaar is als 'M1 = 100%, meestal hebben beide meters ook een lineaire schaal zodat bij andere waarden van % Ml, d.m.v. de bekende formule, de SWR toch nog berekend kan worden.
ON1AFW, Robert Buyle.