Elektromagnetische straling en polarisatie
Maxwell said:
V × E = 0 (1)
V × E = - Bt (2)
V × B = 0 (3)
V × B = εoµ0Et (4)
and there was light!
Maar er kwam meer. Door zorgvuldige bestudering van deze relaties voorspelde Maxwell de radiogolven. De mensheid kan nu niet meer zonder en wij al helemaal niet. Ook tekenen deze wetten voor het bestaan van rontgenstralen en maakten ze, wat recenter ontdekt, de 3K achtergrondstraling mogelijk.
U begrijpt het al. De wetten van Maxwell zijn de fundamenten waarop de elektromagnetische golftheorie gehuisvest is.
Een elektromagnetische golf bestaat, hoe kan het ook anders, uit een elektrische en magnetische komponent. Deze twee komponenten staan loodrecht op elkaar en voor het beschouwen van de golven kijken we alleen naar de elektrische komponent. (De hele golf is zo bepaald: Met de 'kurketrekker-regel' geldt dat de voortplantingsrichting gevonden wordt door over de kleinste hoek van E naar B te draaien.) Iedere oplossing van de Maxwell-vergelijkingen stelt een mogelijke elektromagnetische golf voor. Een algemene oplossing van deze vergelijkingen ligt niet binnen de mogelijkheden van een dergelijk artikel, maar ik wil de oplossing bekijken waarbij het elektrische veld geheel in de Y-richting wijst en als grootte
E = A sin k(x - ct) (5)
heeft. Hierin is A de amplitude van de golf, c de snelheid van het Licht en k = 2π/λ het golfgetal, dat de frequentie van de trilling vastlegt.
Met behulp van (2) volgt dat B = E/c. De uitwijking is in de Z-richting. Het min-teken in (5) geeft aan dat de golf zich naar rechts voortplant. De golf is periodiek in zowel de plaats als de tijd. De plaatsperiodiciteit is uit figuur 1 of te lezen, voor de tijdsperiodiciteit zou ik een reeks opeenvolgende situaties, bijv. t = 0, t = π/2c, t = π/c, t = 3π/2c etc. moeten tekenen.
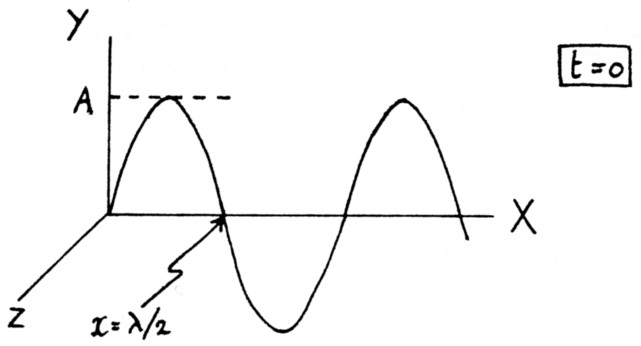
Fig. 1.
In het beschreven geval ligt de uitwijking van het elektrische veld geheel in een vlak. Vandaar dat deze golven vlakke golven worden genoemd. Normale radiogolven zijn vlakke golven. In de vrije ruimte is er maar een soort, maar omdat we op aarde rondwandelen onderscheiden we er twee. Wanneer het elektrische veld evenwijdig aan het aardoppervlak loopt, spreken we van horizontaal gepolariseerde golven, staat het loodrecht op de aarde dan heten het vertikaal gepolariseerde golven. De meeste door ons geproduceerde straling heeft een mengvorm en ligt bijvoorbeeld dichter bij horizontale dan vertikale polarisatie.
Op dezelfde manier als zojuist kunnen we ons ook een golf voorstellen, met een uitwijking in de Z-richting:
E = A cos k(x-ct) (6)
De vergelijkingen (5) en (6) voldoen allebei aan de relaties van Maxwell en dus moet ook de vektoriele som
E = E(Y) + E(Z) (7)
een oplossing zijn. We kunnen nu niet spreken van de richting van het elektrische veld, daar deze afhangt van zowel plaats als tijd.
De golf die we gekreeerd hebben is cirkulair gepolariseerd, zie figuur 2. Men kan zich hem het best voorstellen zoals de draden van een spoel liggen. Bij cirkulair gepolariseerde golven zijn er, zelfs in de vrije ruimte, twee mogelijkheden: de golf kan linksdraaiend, zoals in fig. 2, of rechtsdraaiend zijn.
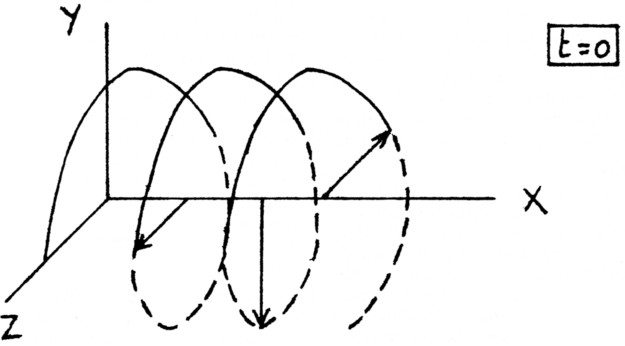
Fig. 2.
Cirkulair gepolariseerde golven komen we ook nog wel eens tegen.
Satellietgebruikers zijn er ongetwijfeld vertrouwd mee, maar ook de helical-antenne is cirkulair gepolariseerd. We kunnen de draairichting veranderen door de voedingspunten om te draaien.
In (7) waren de amplitudes van de op te tellen golven gelijk. Dit hoeft natuurlijk niet en door twee verschillende amplitudes te nemen ontstaan de elliptische golven. Voor zover mij bekend, vinden deze golven geen toepassing.
Waarom zijn deze harmonische golven, zoals (5) en (6) worden genoemd, nu van belang? Allereerst omdat het leeuwendeel van de elektromagnetische golven ermee kan worden beschreven. Zowel laserstralen als een ruiserig CW-station in de 160 meter-band worden globaal gekarakteriseerd door harmonische golven. Maar ze zijn ook van verder theoretisch belang.
Fourier heeft aangetoond dat iedere begrensde en periodieke funktie beschreven kan worden met de som van een konstante en een reeks sinussen en cosinussen. Zo geldt voor de blokgolf uit figuur 3 dat hij is opgebouwd uit:
1 + sin(πx) + ⅓ sin(3πx) + ⅕ sin(5πx) ....
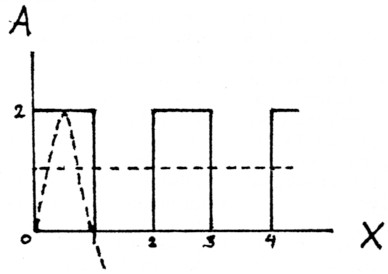
Fig. 3.
Op dezelfde wijze kan een elektromagnetische golf, na hem in een Y- en een Zkomponent te hebben verdeeld, ontbonden worden en is dan met (5) en (6) volledig te beschrijven. De konstante noemen we nul door ons assenstelsel op de juiste plaats te kiezen.
De praktijk
In theorie bestaat er dus geen verschil tussen horizontaal en vertikaal gepolariseerde golven. Voor lage frequenties, tot ± 30 MHz, is op lange afstand echter alleen de vertikale komponent bruikbaar omdat de aarde de horizontale komponent te sterk dempt. Verder is de invloed van geloniseerde luchtlagen zo groot dat er van de oorspronkelijke polarisatie weinig overblijft. Boven de 30 MHz is voor DX-verkeer horizontale polarisatie gebruikelijker. Menselijke stoorsignalen, zoals van motoren, zijn overwegend vertikaal gepolariseerd, zodat horizontale polarisatie zwakkere signalen hoorbaar kan maken. Een bijkomend voordeeltje is dat heuvelachtig terrein licht de neiging heeft golven horizontaal te maken. Alleen bij sporadische E blijft de polarisatie slecht behouden. Voor lokaal gebruik is vertikale polarisatie in zwang, omdat antennes daar eenvoudig voor te konstrueren zijn. Om via satellieten te kunnen werken moet de golf enorme afstanden afleggen. Er treedt dan een polarisatiedraaiing op en in die gevallen is cirkulaire polarisatie superieur. Wanneer de ontvangst- en zendantenne qua draairichting niet bij elkaar passen, wordt u gestraft met een verlies van 20 dB, net als het verschil tussen vertikaal en horizontaal trouwens. Een cirkulair gepolariseerde antenne ontvangt vlakke golven, zowel horizontaal als vertikaal, met een verlies van 3 dB.
Tot slot een kritische kanttekening. De wetten van Maxwell, zoals geponeerd in (1) t/m (4) zijn alleen geldig in vakuüm waar zich geen lading of stroom bevindt. Ze vormen voor onze atmosfeer echter een goede benadering. Verder pretendeer ik niet de wijsheid in pacht te hebben en hou me dan ook aanbevolen voor zowel aanvullingen als kritiek.
Literatuur
- Alonso/Finn: 'Fields & Waves' (1979) CCIR: Report 227 (1978)
PA3FAQ.