Nader bekeken: Het PI-filter
Heeft u ook al eens een PI-filter berekend of bent u daar nooit aan begonnen, geschrokken nadat u in ieder leerboek steeds andere en dan ook nog heel ingewikkelde formules tegenkwam? dan moet u nu verder lezen.
Het kan anders, het kan simpel!
Stel u voor een autotrafo (fig. 1), de impedanties van N1 en N2 verhouden zich als de wikkel verhoudingen in het kwadraat (C-examen). Bij de trafo met kapacitieve aftakking is dit niet anders (fig. 2). Het PI-filter is een gekantelde trafo met kapacitieve aftakking (fig. 3).
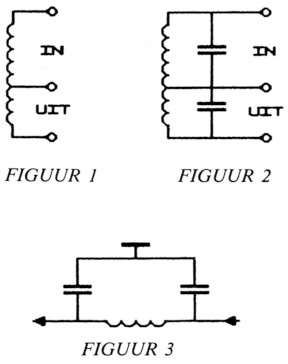
Als rekenvoorbeeld wordt hier het onderstaande PI-filter berekend.
R-in : R-uit als 5000 : 50 = 100 : 1, de transformatieverhouding is dus 10 : 1. Als we Cuit dezelfde impedantie geven als R-uit wordt X-uit, na vektorisch optellen, ca 35 Ohm (50/√2).
X-in, de andere 'winding' van de trafo, zal bij de gewenste transformatieverhouding 10 × zo groot moeten zijn, dus 350 Ohm.
De totale impedantie van de trafo wordt dan dus 35 + 350 = 385 Ohm(1).
Teneinde de in- uitgang 'zuiver' Ohms te krijgen moet de kapacitieve belasting van C-in en C-uit teniet worden gedaan met een even grote zelfinduktie. De spoel krijgt dus een impedantie van 385 Ohm, wat voor b.v. de 29 MHz werkfrequentie neerkomt op ± 2 µH(2).
Een spoel met deze waarde kan met een dipper worden gemaakt (15 MHz/50 pF)(2). Xc-uit = 35 Ohm, voor 29 MHz wordt dat 150 pF(2). Neem hiervoor een variabele C die iets groter in waarde is (200 pF). Xc-in = 350 Ohm, C-in is dan 15 pF(2) (trimmer 25 pF). Dit PI-filter werd in een 10 meter buizen eindtrap gemonteerd en na afgesloten te zijn met 50 Ohm nagemeten met de probe uit CQ-PA nr. 5-1988. Het klopte: U-in = 10x U-uit!
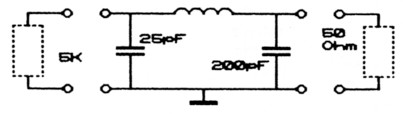
Fig. 4.
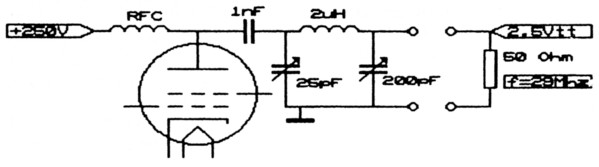
Fig. 5.
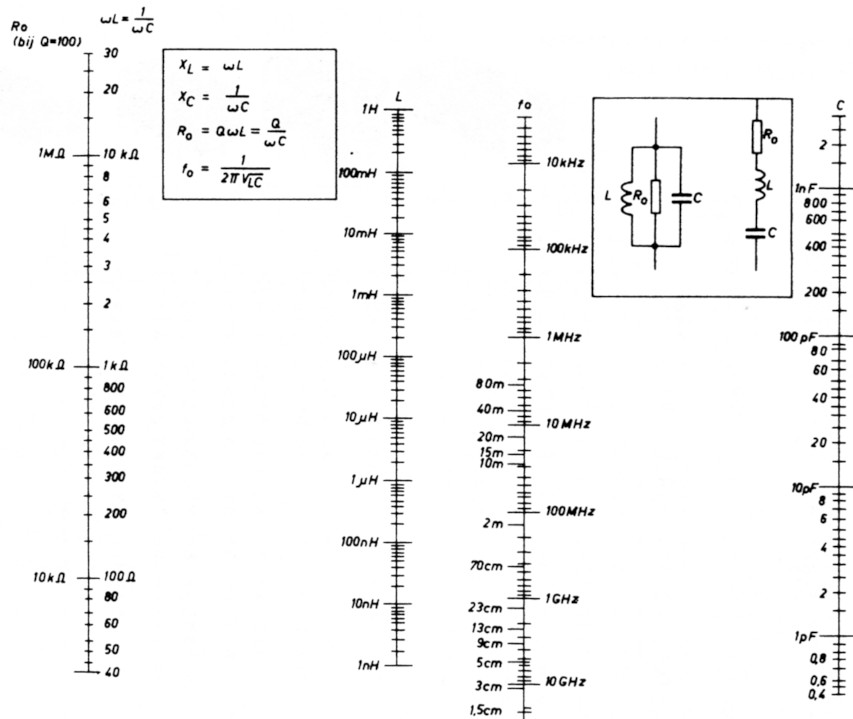
Nomogram voor serie- en parallelkringen.
Notes
- Hier had eigentijk met spanning moeten worden gerekend, maar aangezien de stroom door de trafowikkeling gelijk blijft is er niets op tegen hier met weerstand te rekenen.
- Niet berekend maar met een 'nomogram' bepaald.
PE1MJS.