Aanpassen via de kabel
Zoals bekend is een juiste impedantie-aanpassing essentieel voor het optimaal functioneren van iedere zend/ontvangst installatie. Niettemin blijkt er in de amateurwereld aangaande dit onderwerp een flink aantal misverstanden te bestaan.
Met name de rol die de antennekabel hierbij speelt is voor velen nogal duister. Op zich is dat niet zo vreemd, want het is niet zo eenvoudig om de ingangs-impedantie van een willekeurig afgesloten kabel te berekenen. Zeker niet wanneer we daarbij ook nog rekening houden met de kabelverliezen. Hier ligt dan ook een schone taak voor onze elektronische rekenslaaf: de computer. Naar aanleiding van een interessante discussie met Bastiaan PA3FFZ ontstond het idee om een eerder geschreven eenvoudig BASIC programmaatje om te zetten naar Pascal om er vervolgens nog een snuifje gebruiksvriendelijkheid en een schepje opties aan toe te voegen. Het resultaat: ZIN (spreek uit zet in) Voordat ik inga op de werking van het programma is het wellicht goed om eerst nog eens wat theorie op te halen.
Aanpassing
Bij impedantie- of beter gezegd vermogens-aan passing (er bestaat ook nog zoiets als ruis-aanpassing) draait het om de vraag hoe aan een gegeven spanningsbron een zo groot mogelijk vermogen kan worden onttrokken. Zoals bekend bezit iedere praktische spanningsbron een inwendige weerstand (impedantie). Voor zuiver Ohmse impedanties is eenvoudig aan te tonen dat het afgegeven vermogen maximaal zal zijn wanneer de belastingsweerstand gelijk is aan de inwendige weerstand van de spanningsbron. In de praktijk hebben we echter niet altijd te maken met zuiver Ohmse impedanties. Wanneer de antenne niet geheel, of geheel niet in afstemming is zal de impedantie ervan complex zijn: d.w.z. zowel een zuiver Ohmse als een reactieve (Inductieve of Capacitieve) component bevatten.
Aangezien reactieve componenten geen vermogen dissiperen vormen ze slechts een obstakel voor het bereiken van een maximale vermogensoverdracht.
Daarom geldt dat voor een optimale vermogensaanpassing, niet alleen de Ohmse componenten van bronen belastings-impedantie even groot moeten zijn, maar tevens dat de som van de reactieve componenten van bron- en belastings-impedantie nul dient te zijn. Een goed voorbeeld van het 'wegresoneren' van een reactieve (in dit geval capacitieve) component van de antenne-impedantie is de toepassing van een verlengspoel bij (te) korte mobielantennes. Dit 'wegresoneren' van reactieve cornponenten wordt vaak gezien als het afstemmen van de antenne. Strikt genomen is dit niet juist! De resonantiefrequentie van een antenne wordt uitsluitend bepaald door de afmetingen van de antenne.
Met het toevoegen van een capacitieve of inductieve impedantie wordt de antenne zelf niet in resonantie gebracht, maar wordt slechts bereikt dat de combinatie van antenne en b.v. verlengspoel of antennetuner een zuiver Ohmse impedantie oplevert.
Reflecties
Met uitzondering van portofoons is het om praktische redenen niet gebruikelijk om een transceiver direct op de antenne aan te sluiten. In pleats daarvan wordt de antenne via een kabel met de transceiver of ontvanger verbonden. Zoals bekend be-zit ook de antennekabel een bepaalde impedantie: de karakteristieke impedantie. Deze impedantie is afhankelijk van de constructie van de kabel ; de afmetingen en onderlinge afstand van de geleiders, en de dielektrische constante van het isolatiemateriaal.
Wanneer we aan het uiteinde van een kabel een spanningsbron aansluiten zal een gecombineerde spannings- en stroomgolf ontstaan die zich met een bepaalde sneiheid in de richting van het andere uiteinde voortplant. De verhouding tussen spanning en stroom in deze golf is gelijk aan de karakteristieke impedantie van de bewuste kabel. Aangezien spanning en stroom in deze lopende golf met elkaar in fase zijn gaat het hier om een zuiver Ohmse impedantie.
Wat gebeurt er nu als de golf het eind van de kabel bereikt?
Wel, laten we eens aannemen dat de kabel is afgesloten met een impedantie die hoger is dan de karakteristieke impedantie van de kabel. Een dergelijke impedantie zal bij de gegeven spanning niet alle aangevoerde stroom accepteren. Het stroom-overschot kan slechts worden afgevoerd door een tweede lopende golf die zich in terugwaartse richting voortplant. Aangezien spanning en stroom ook hier weer gekoppeld zijn via de karakteristieke impedantie van de kabel, betekent dit dat een gedeelte van het toegevoerde vermogen wordt gereflecteerd. Een soortgelijke situatie ontstaat ook wanneer de kabel wordt afgesloten met een impedantie die lager is dan de karakteristieke impedantie van de kabel, of wanneer de afsluit-impedantie niet zuiver Ohms is. In het laatste geval ontstaat een faseverschil tussen spanning en stroom, waardoor ook dan het toegevoerde vermogen niet volledig door de belasting wordt opgenomen. De sterkte van de
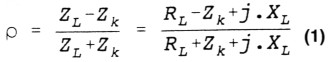
gereflecteerde golf wordt bepaald door de reflectie coefficient p die als volgt berekend kan worden waarin RL en XL resp. de Ohmse en reactieve component van de belasting, en Zk de karakteristieke impedantie van de kabel voorstellen. ρ is dus in het algemeen complex. De absolute waarde van ρ kan berekend worden uit:
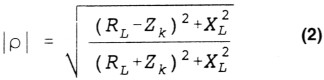
De sterkte van de gereflecteerde spanning- en stroom-golf wordt nu gegeven door Uref = |ρ|2 × Pheen en Iref = |ρ| × Pheen (althans wanneer wordt verondersteld dat de stroom voor zowel de heengaande als gereflecteerde golf in dezelfde richting loopt). Het gereflecteerde vermogen is derhalve gelijk aan:
Pref = |ρ|2 × Pheen.
S.W.R.
De totale spanning of stroom op iedere plek in de kabel is de som van de spanning en stroom van zowel de heengaande golf als de gereflecteerde golf.
Tussen heen- en teruggaande golf bestaat echter een faseverschil dat plaatsafhankelijk is. Op sommige plaatsen zullen de heen- en teruggaande golven elkaar versterken, terwijI ze elkaar op andere plaatsen juist verzwakken. Op deze manier ontstaat een zogenaamd staande golf patroon. Doordat de reflectiecoefficient voor spanning en stroom in feite van teken verschilt (zie boven) zullen in dit patroon spanningsbuiken samenvallen met stroomknopen en omgekeerd stroombuiken met spanningsknopen. Dit betekent dat ook de impedantie van plaats tot plaats verschillend zal zijn. (Hierover later meer.)
Zoals gezegd varieren spanning en stroom langs de kabel tussen een maximum en een minimum waarde. De verhouding tussen dit maximum en minimum noemen we de staande golf verhouding (of Standing Wave Ratio: SWR). Dit is tevens een maat voor de misaanpassing.
De maximum waarde vinden we door de heen- en teruggaande golven bij elkaar op te tellen, dus b.v.: U(1 + p) en de minimumwaarde door beide golven van elkaar of te trekken: U(1 - p). Hieruit volgt voor de staande golf verhouding:
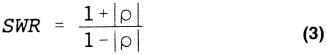
Praktijk
Genoeg theorie en enge formules. Laten we ons eens verdiepen in de praktijk.
In de meest ideale situatie hebben we te maken met een lopende aanpassing; d.w.z. een transceiver met een in- en uitgangsimpedantie van b.v. 50 Ω is aangesloten op een 50 Ω coax kabel, welke vervolgens is verbonden met een resonante antenne met een stralingsweerstand van 50 Ω. Geen reflecties, geen ellende: perfect. Deze situatie is voor mono-band antennes vaak redelijk te benaderen. Een afwijkende stralingsweerstand wordt met behulp van b.v. een gamma match, balun, kwart lambda trafo of op andere wijze ter plaatse van de antenne aangepast aan de karakteristieke impedantie van de antennekabel.
Voor VHF en UHF is dit eigenlijk ook de enige juiste manier, maar voor de HF banden gelden andere overwegingen. Zo is het uiterst onpraktisch om voor iedere band een aparte antenne te installeren. Daarom wordt vaak gebruik gemaakt van een draadantenne, die met behulp van een antennetuner (door sommige minder verlichte geesten ook wel 'kassie belazer' genoemd) op iedere band kan worden aangepast. Omdat het altijd een goede zaak is om het kwaad bij de wortel aan te pakken ligt het voor de hand om de tuner tussen de antenne en de kabel aan te sluiten. Dit levert echter, vooral wanneer we gebruik maken van zo'n automatische antennetuner, een ietwat onhandige configuratie op.
Daarom is het gebruikelijker om de tuner aan het andere eind van de kabel, tussen de transceiver en de antennekabel aan te sluiten.
De vraag is echter of dit zonder meer is toegestaan, en of hiermee inderdaad een optimale aanpassing kan worden gerealiseerd.
Verliesvrije kabel
Laten we er eens vanuit gaan dat de antenne is aangesloten op een stuk verliesvrije kabel, en dat de impedantie van de antenne kan worden geschreven als Za = Ra + j.Xa. Aan het andere uiteinde van de kabel meten we in dat geval een impedantie Zb = Rb + j.Xb. Deze impedantie is niet alleen afhankelijk is van Za, maar ook van de elektrische lengte van de kabel (dus rekening houdend met de verkortingsfactor van de kabel), de frequentie en de karakteristieke impedantie van de kabel. Wanneer we nu de antennetuner zo instellen dat diens uitgangsimpedantie Zt gelijk is aan Rb - j.Xb, dan zal het volledige beschikbare vermogen aan de combinatie kabel/antenne worden afgegeven. Aangezien er in de kabel zelf geen verliezen optreden betekent dit tevens dat al het vermogen door de antenne zal worden opgenomen. Dit is slechts mogelijk wanneer de antenne wordt gevoed vanuit een impedantie die gelijk is aan Ra - j.Xa. Berekeningen tonen aan dat wanneer de kabel wordt afgesloten met Zt = Rb - j.Xb de impedantie die we aan het andere uiteinde meten inderdaad geljk is aan Ra - j.Xa. Met andere woorden, door aan de transceiverzijde te zorgen voor een optimale aanpassing aan de daar heersende impedantie, wordt automatisch bereikt dat ook aan de antenne de juiste impedantie wordt aangeboden. Voor alle duideIijkheid: er is geen sprake van aanpassing tussen tuner en karakteristieke impedantie van de kabel, noch van aanpassing tussen kabel en antenne. Het gevolg is dan ook dat er zowel op de overgang van tuner naar kabel als op de overgang van kabel naar antenne reflecties zullen ontstaan. Bij de bovenstaande procedure wordt de tuner echter zo ingesteld dat de reflectie aan de uitgang van de tuner even groot doch in tegenfase is met de reflectie afkomstig van de antenne.
Deze twee reflecties heffen elkaar dus op, zodat uiteindelijk toch sprake is van een optimale aanpassing.
Meervoudige reflecties
Oplettende lezers zullen aanvoeren dat ik in het voorgaande geen rekening heb gehouden met het feit dat de reflectie van de antenne opnieuw gedeeltelijk zal worden gereflecteerd door de tuner. In werkelijkheid zullen we dus te maken hebben met een oneindig aantal weliswaar steeds zwakker wordende golven die voortdurend door de kabel heen en weer pendelen.
Laten we deze situatie eens nader bekijken. Een spanningsbron met een bronspanning V en een inwendige impedantie Z is aangesloten op een niet karakteristiek afgesloten stuk kabel met een karakteristieke impedantie Rk.
Z wordt zodanig gekozen dat er een optimale aanpassing tussen bron en kabel plus belasting ontstaat. Dit betekent tevens dat de reflectiefactoren ρ1 en ρ2 resp. aan het begin en het eind van de kabel even groot, doch vanuit de kabel gezien tegengesteld van teken zijn. Vlak na het aanschakelen van de bron bedraagt de ingangsspanning Vi van de kabel:

Een factor ρ van deze ingangsspanning keert na reflectie bij de belasting weer terug bij de bron. Hier ontstaat opnieuw een gedeeltelijke reflectie, waardoor een factor ρ2 opnieuw in de richting van de belasting vertrekt, enz. enz.
Door alle, bij de ingang terugkerende en vertrekkende reflecties bij elkaar op te tellen kunnen we de spanning Vu die uiteindelijk op de ingang van de kabel zal staan berekenen:

De som van reflecties aan de ingang bedraagt:

Wiskundig kan worden afgeleid dat:
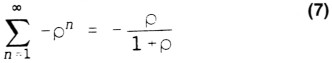
Tellen we alle reflecties op bij de oorspronkelijke ingangsspanning dan vinden we de spanning die uiteindelijk aan de ingang zal ontstaan:
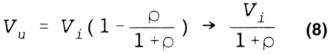
Vervangen we Vi door (4) en ρ door (5) dan volgt:
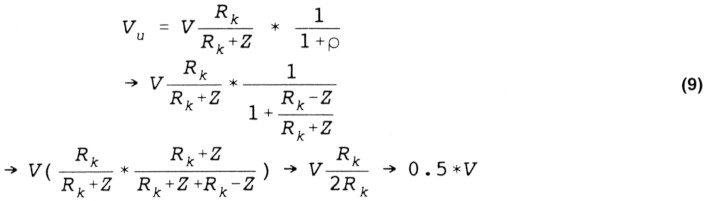
Oplettende lezers die inmiddels nog niet zijn afgehaakt zullen hieruit met mij concluderen dat de bron door de combinatie van kabel en belasting inderdaad karakteristiek is afgesloten. Met andere woorden: het is volstrekt toegestaan om meervoudige reflecties buiten beschouwing te laten!
Verliezen
Terugkerend uit het nirvana van de wiskunde moeten we echter constateren dat energietransport via kabels in praktijk wel altijd gepaard gaat met verliezen.
Hierdoor worden zowel heengaande als gereflecteerde golven in zekere mate gedempt. Het gevolg is dat de reflecties van de antenne en van de overgang van tuner naar kabel elkaar niet langer zullen opheffen. Door de tuner anders in te stellen kan weliswaar worden bereikt dat er aan de ingang van de kabel een perfecte aanpassing ontstaat, maar dit betekent niet langer dat ook de antenne perfect is aangepast (hetgeen bij verliesvrije kabels wel het geval was).
Karl Rothammel beschrijft in z'n onvolprezen Antennen Handbuch dat door de staande golven op de kabel extra verliezen optreden: ter plekke van een stroombuik zouden er extra koperverliezen, en ter plekke van een spanningsbuik extra dielektrische verliezen optreden. In feite is zijn beschrijving uiterst misteidend: Het extra verlies wordt niet veroorzaakt door het optreden van staande golven (immers wat te denken van de geringere verliezen in de spannings- en stroomknopen), maar doordat we er simpelweg niet meer in slagen om de antenne optimaal aan te passen.
Overigens merkt Karl terecht op dat het met die verliezen in praktijk doorgaans wel mee zal vallen. Pas bij een relatief hoge SWR zullen de extra verliezen uitstijgen boven de kabeldemping die ook bij een perfecte aanpassing op zou treden.
Kassie belazer?
In de inleiding sprak ik at over de misverstanden die er bestaan ten aanzien van een aantal onderwerpen die te maken hebben met aanpassing.
Een veel gehoorde opvatting is dat je jezelf alleen maar voor de gek houdt wanneer je een antennetuner tussen de transceiver en de antennekabel toepast.
Volgens velen zou het minimaliseren van de SWR tussen transceiver en tuner er slechts toe dienen om te voorkomen dat het vermogen uit de eindtrap wordt teruggeregeld. De hoge SWR op de antennekabel wordt hierdoor niet beInvloed, en dus zou er ook geen sprake kunnen zijn van een optimale aanpassing. Dit misverstand wordt waarschijnlijk ingegeven door een heilig geloof in de noodzaak van een lage SWR. Dit is waarschijnlijk tevens de reden waarom veel OM's een diepgeworteld wantrouwen koesteren ten aanzien van de aanwijzing van hun staande golf meter.
Zotang echter de kabelverliezen beperkt blijven, en dat is op de HF banden vrijwel altijd het geval, kan een antenne m.b.v. een tuner goed worden aangepast. Een hoge SWR op de antennekabel is in dat geval helemaal niet erg, en is zeker geen bewijs dat de aanpassing niet deugt!
Het argument dat de tuner, ook wanneer er geen antenne op de uitgang is aangesloten, op minimale SWR kan worden afgeregeld pleit niet voor de bouwer van de betreffende tuner.
Dit effect kan namelijk alleen worden verklaard door te veronderstellen dat in de tuner zelf behoorlijke verliezen optreden. Bij de bouw van een antennetuner dient men altijd (ook voor kleine vermogens) gebruik te maken van dik, liefst verzilverd draad. Verder is het van belang om ervoor te zorgen dat contacten van schakeleers en dergelijke een zo klein mogelijke overgangsweerstand vertonen. Wanneer op die manier de verliezen in de tuner zijn geminimaliseerd zal het beslist niet zo eenvoudig meer zijn om een lage SWR te bereiken wanneer de tuner niet wordt belast.
Stralende kabels
Een ander misverstand is dat door het optreden van staande golven kabels zouden gaan stralen. Een kabel kan slechts gaan stralen wanneer er sprake is van ongelijke stromen in de beide geleiders. Hoewel bij staande golven stroom- en spanningsmaxima niet samenvallen blijven de stromen in de geleiders op ieder stukje kabel wel gelijk, en kan er dus geen sprake zijn van uitstraling door de kabel zelf. Dit geldt zowel voor coaxiale als voor symmetrische kabels!
Als een antennekabel blijkt te stralen is dit altijd terug te voeren op een foutieve symmetrie en/of slechte aarding.
Coax versus symmetrisch
Vaak wordt beweerd dat een antenne niet via een coax kabel kan worden aangepast, terwip dit bij een symmetrische kabel wel zou lukken. In principe is deze stelling onjuist. Toch zit er wel een kern van waarheid in.
Zoals ik omstandig heb uitgelegd spelen de verliezen van de antennekabel een belangrijke rol. Nu is het zo dat met name op hogere frequenties coax kabels aanmerkelijk meer verlies geven dan symmetrische voedingslijnen.
Dit komt doordat bij hogere frequenties de dielektrische verliezen van het isolatiemateriaal een belangrijke rol gaan spelen. Bij symmetrische voedingslijnen, zoals de bekende home-made kippenladders, bestaat het dielektricum voornamelijk uit lucht. Hierdoor blijven de dielektrische verliezen bij dit soort kabels uiterst beperkt.
Verder is het zo dat de karakteristieke impedantie van coax kabels over het algemeen betrekkelijk laag is, zeker in vergelijking met zelfgemaakte kippenladders, waarvan de impedantie doorgaans een paar honderd Ohm bedraagt.
Deze waarde stemt wat beter overeen met de antenne impedanties die we zoal tegen kunnen komen: varierend van enkele tientallen Ohm tot een paar kiloOhm. Het gevolg is dat de SWR op een symmetrische lijn gemiddeld genomen lager zal zijn dan bij coax kabels, zodat ook hierdoor de verliezen beperkt blijven. Dit alles neemt echter niet weg dat in veel gevallen (bij niet at te extreme antenne impedanties) aanpassen via een coax kabel zonder meer mogelijk is. Overigens moet hierbij wel worden opgemerkt dat, wanneer voor het aansluiten van een symmetrische antenne op een coax kabel gebruik wordt gemaakt van een breedbandige ringkern balun, de nodige complicaties kunnen ontstaan. Met name bij hoge antenne-impedanties bestaat het gevaar dat de ringkern in verzadiging raakt. Het gevolg is oververhitting en permanente beschadiging van de balun.
Arend Harteveld, PA-9782 (PEIPVB).