Elke dag een nieuwe horizon
Leren ze het dan nooit? !@?%!]
Iedereen schijnt die kreet wel een paar maal in z'n leven te slaken. Nou, beste radiovrienden, aan mij is hij ook wel eens ontsnapt. En wel naar aanleiding van vraag 46 van het afgelopen C-examen.
C-46: Vanuit een ballon op 300 meter hoogte boven het aardoppervlak ligt voor VHF-communicatie de radiohorizon op ongeveer:
A. 10 km
B. 50 km
C. 200 km
D. 1000 km
Hum, 'ze' zeggen 200 km (antwoord C). Dat is wel een boel, maar het zou misschien kunnen; 300 m is tenslotte wel erg hoog.
"Kan ik dat ook op de een of andere manier uitrekenen?", wilde mijn kandidaat weten. Ja, daar is een fraaie formule voor... iets met de wortel uit hoogte maal een of andere constante , drie-komma-zoveel. Maar dat weet ik niet uit mijn hoofd. Kijk maar in een goed cursusboek, daar vind je het wel.
Eerlijk gezegd had ik toen nog niet het gevoel dat er 'bloed' uit dit vraagstuk liep. Dat kwam pas bij het nabespreken. Mijn kandidaat had zich gewapend met een (redelijk) modern cursusboek (VERON, 1983) terwijl ik mij voor moeilijke gevallen wend tot een oud boek uit 1972. Dat oude boek geeft een complete afleiding en de factor drie-komma-zoveel blijkt 3,56 te zijn.
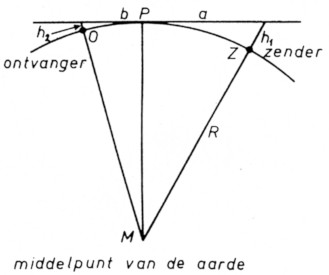
In de driehoek MPZ geldt:
a2 + R2 = (h1 + R)2 = h12 + 2h1 + R2
a2 = h12 + 2h1R = h1(h1 + 2R)
Ten opzichte van de middellijn van de aarde 2R kan de hoogte h1 van de antenne verwaarloosd worden, zodat ook kan worden geschreven:
a2 = 2R × h1
a = √h1 × 2R
2R = 12740 km
a = 3,56√h1
b = 3,56√h2
De totale direktzicht afstand wordt a + b = 3,56 (√h1 + √h2) km
De afstand in kilometers en de hoogte in meters.
Het is een eigenaardige formule met de hoogte in meters en de afstand in kilometers. Dat doen we even: 3,56 × 4300 = 61,7 km. He??? Dat komt in de buurt van antwoord B!!
Inmiddels heeft mijn kandidaat het 'moderne' boek erbij gepakt. De factor 3,56 is inmiddels 'opgewaardeerd' tot 4. Kijk, we hebben inmiddels de flower-power tijd achter ons. Ik zie de dingen tegenwoordig een stuk verder dan vroeger en dan schuift je radiohorizon ook een stukje op... helemaal tot 69,3 km. Maar het 'goede' antwoord 'C' van 200 km komt voor geen meter in beeld.
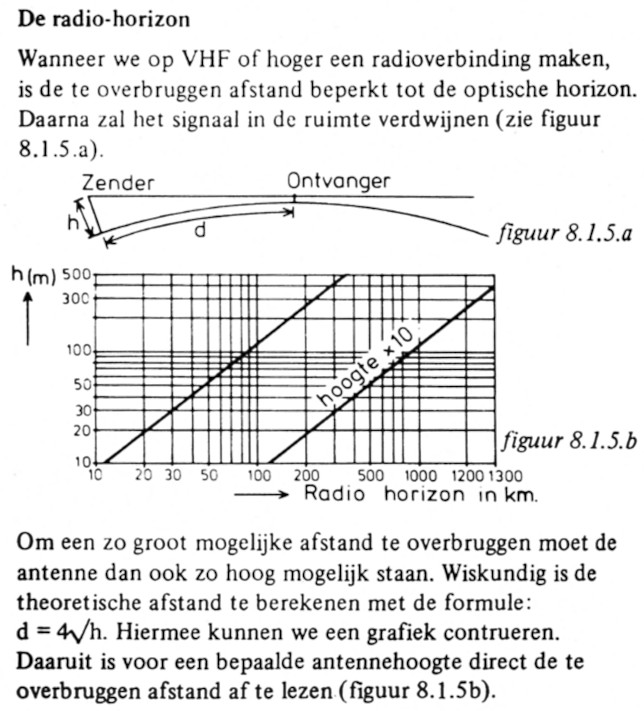
Maar nu gaat mijn kandidaat met figuur 8.1.5b aan de slag.
Kijk dan, op de verticale as ga ik bij 300 meter naar rechts tot ik die dikke lijn snijd. Van daaruit ga je verticaal omlaag en dan lees ik een afstand of van zo'n 250 km!
Waaaat!!! Ik kan nog net een krachtterm onderdrukken. Hier schuift je radiohorizon wel even van op zeg. Zo kun je nog eens leuke afstanden draaien met je 2m-setje!
To 'grafiek' or not to 'grafiek'...
Bij nadere beschouwing vinden jullie misschien dat de schaalverdeling van fig. 8.1.5b er een beetje eigenaardig uitziet. Dit is een log-log schaal. Het aardige van zo'n schaal is dat heel wat formules die er in een gewone (lineaire) grafiek niet zo gemakkelijk uitzien, zich voor laten stellen door een rechte lijn en dat is natuurlijk een stuk handzamer. 'Krities' ingestelde lieden zouden zeggen dat we een moeilijke lijn vervangen door een moeilijke schaalverdeling. (In de flower-power tijd moest je 'Icrities' echt zo spellen.)
In de praktijk komt het er op neer dat de exponent (die in de formule verscholen zit) wordt vertaald in de hellingshoek van de lijn. Stel: ik heb een formule van de vorm y=x2 (een parabool). In een log-log grafiek wordt dat een rechte lijn met een hellingshoek van 63° (richtingscoefficient 2). Met y=x wordt het een rechte lijn onder 45° (richtingscoefficient 1) en y=√x geeft een rechte lijn onder 27° (richtingscoefficient ½). Dat is dus de lijn die we voor de formule d=4√h zouden verwachten, maar de lijnen in figuur 8.1.5b lopen ongeveer onder 45°! De makers van deze figuur hebben vast de zomer in het hoofd gehad want het lijkt wel of ze bij het 'vertalen' van de formule naar de grafiek, het wortelteken geschrapt hebben. Je durft het toch bijna niet te denken he... maar zou de examencommissie zich bij het opstellen van vraag 46 hebben laten leiden door dit figuurtje? Tja, dan leren ze het nooit.
Wat ik zo mogelijk nog beroerder vind: hoe moet een examenkandidaat zich hier uitredden? Het probleem begint al bij de opgave. Als ik die lees denk ik in de eerste plaats aan rechtlijnige voortplanting. Dus wil ik de formule b=3,56√h toepassen. Dat klopt natuurlijk niet helemaal want een VHF-signaal buigt nog wel een beetje met de aardkromming mee. Bovendien: wat is VHF? 144 MHz? Daarmee kijk je nog wel een stukje over de optische horizon. Maar 50 MHz is ook VHF en daarmee kijk je een stuk verder. Moet ik dat meenemen of niet? En tenslotte: wat is de gevoeligheid van je ontvanger? Je bent het tegenstation immers pas kwijt als het signaal zakt onder het ruisvermogen van de ontvanger...
Als men nu eens begon om het vraagstuk eenduidig te maken. Bijvoorbeeld:
Een zendantenne staat op 300 m hoogte. De radiohorizon bedraagt bij rechtlijnige voortplanting ongeveer: ?
Vervolgens zorg je nog voor een 'goed' antwoord en klaar is Kees. Wie weet leren 'ze' het op een dag toch nog.
Joop, PA3BMV.