Spoelen wikkelen
"Ik heb een spoel en nu wil ik op een lagere frequentie gaan werken. Er zal dus een nieuwe spoel gewikkeld moeten worden of aan de bestaande spoel lets moeten worden veranderd. Wie weet hoe dat moet... een spoel wikkelen? Kent iemand de formules daarvoor?"
En toen werd het stil
Wonderlijk eigenlijk. Het is toch een probleem waar menige zelfbouwer tegen aanloopt. Alles is te koop... zegt men. Dus gaan we niet zelf aan de slag. Weerstanden zou je zelf kunnen maken en condensatoren ook. De kwaliteit en de afmetingen zijn echter van dien aard dat het zelf maken van deze onderdelen echt niet loont. Met spoelen ligt dat toch even anders. Er is wel-is-waar een groot aantal spoelen en trafo's in de handel maar... lang niet over-al en bovendien vaak slecht gecodeerd, voor speciale toepassingen, met de verkeerde aftakkingen of gewoon te klein.
Soms kan men het probleem oplossen door aan een bestaande spoel die veranderd moet worden extra spoelen parallel of in serie te schakelen. Zo heb ik een MG autoradio naar de 10 MHz-amateurband omgezet door parallel aan de oscillatorspoel met "verschuifbare kern afstemming" (permeabiliteits-afstemming) een klein spoeltje te schakelen. De waarde van dit spoeltje kan berekend worden met de formule die we ook gebruiken voor het parallel schakelen van weerstanden. Eerst moet dan wel de waarde van de oorspronkelijke spoel worden vastgesteld. Meten is weten... maar daar moet je dan wel de apparatuur voor hebben. Rekenen is ook een manier. Ms we de frequentie(s) weten en de parallel-C komen we er met de bekende formule vast wel uit.
Deze formule rekent niet lekker. Het duurt lang voordat je de juiste waarde te pakken hebt en de kans op fouten met het aantal nullen is groot. Ik gebruik dan ook vrijwel altijd het nomogram zoals dat in CQ-PA mei 2000 (blz. 155) is gepubliceerd.
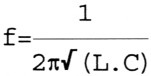
In het geval van de beschreven oscillator is experimenteel te werk gegaan. Verschillende spoeltjes zijn "op goed geluk" geprobeerd totdat het gewenste frequentiebereik gevonden was. Soms geeft rekenen snellere resultaten. Soms proberen. Hier was ook van belang of de oscillator zou afslaan en dat is met proberen eenvoudig na te gaan en met berekenen vrijwel niet.
Met de MF-trafo's uit het Verre Oosten kunnen we ook dit soort grappen uithalen. 50 trafo's voor 455 kHz heb ik nagemeten en 49 daarvan hadden een spoel van 600 µH met een parallel-C van ca 180 pF. Willen we daarin verandering brengen dan is de eenvoudigste manier: een extra C parallel frequentie omlaag. Minder C kan ook: in de voet zit een keramisch buis-Ctje en dat kan men met een klein scherp schroevendraaiertje stukbreken. Uit de genoemde formule volgt dat de frequentie athankelijk is van √(L.C). Maken we C nu 4 × zo klein dan wordt de frequentie 2 × zo hoog. Dus met 45 pF wordt de nieuwe resonantiefrequentie ca 900 kHz.
Met de 10,7 trafo's gaat het net zo. De spoel heeft over het algemeen een waarde van 3 tot 5 µH en de inwendige C een capaciteit van ca 45 pF. Om op 3,6 MHz uit te komen moet een C worden bijgeplaatst (meestal 270 pF) en met het verwijderen van de inwendige condensator zijn frequenties tot ±20 MHz haalbaar. Nog hoger gaat ook nog door het parallelschakelen van een kleine RFC (smoorspoeltje); die dingen die er uitzien als kleine weerstanden. Er zijn heel veel gelegenheden waarbij het bijplaatsen van een extra C of een spoel voor het veranderen van de resonantiefrequentie van een Laing een prima oplossing is. Het vreemde is echter dat we 'het' met condensators allemaal wel eens doen en met spoelen bijna nooit.
Dit systeem - het parallel-schakelen van spoelen - gebruik ik ook in mijn antennetuner. Niet alleen wordt voor de lage banden extra C met een schakelaar bijgezet, voor de hogere frequenties schakel ik een of meer spoelen parallel. Mijn tuner heeft dus niet een spoel met veel aftakkingen maar vier spoelen die in verschillende configuraties parallel kunnen worden geschakeld met simpele wipschakelaars.
Zelf wikkelen
Soms valt er niet aan te ontkomen: we moeten zelf gaan wikkelen, maar hoe luidt de formule voor het zelf wikkelen van spoelen? Ik heb er 3 formules voor kunnen vinden. Ze zijn verschillend en zijn van toepassing op spoelen waar maar in een laag wordt gewikkeld.
De eerste: (bron: W6SAUCQ-PA)
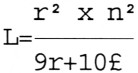
L in µH
r = ½ diameter in inches
n = aantal wdg
£ = bewikkelde lengte in inches
1" = 25,4mm
Voor deze formule die wat ongemakkelijk in inches luidt wordt door W6SAI een nauwkeurigheid geclaimd van 1% tot in de VHF-band.
De tweede: (bron: PEIFWU in Electron)

£ = lengte in cm
L in nH
Deze formule lijkt me niet zo geschikt om een spoel mee te gaan wikkelen maar goed bruikbaar om van een bestaande spoel de zelfinductie te achterhalen. Voor het bepalen van de lengte van het draad is het natuurlijk niet nodig om de spoel of te wikkelen. = n.d.fc met eventueel een paar % erbij als de wikkelingen een grote spatie hebben.
De derde: (bron: Das Spulenbuch, H. Sutaner)

π2 = 9,87
d = diameter in cm
n = aantal wdg
£ = bewikkelde lengte in cm
K = vormfactor uit het nomogram (d/£)
L in H!
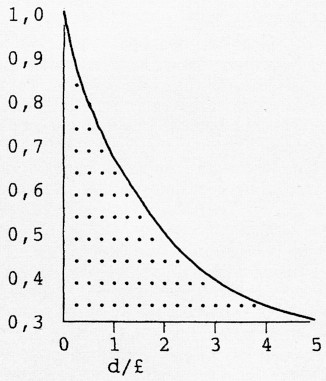
De draaddikte komt u niet tegen in de tot nu toe gegeven formules en die speelt dan ook geen belangrijke rol by het wikkelen. Wel moet het draad natuurlijk op de "bewikkelde lengte" passen.
Kloppen deze formules?
Meten is weten! De grote spoel op de foto (er staat een 9V-batterijtje voor) is gewikkeld als verlengspoel voor een lange golf antenne en heeft een gemeten zelfinductie van 2,8 mH. Er zijn 125 windingen gelegd op een spoellichaam met een diameter van 320 mm en de bewikkelde lengte is 275mm.

Formule 1:
r = 160 mm = 6,3"n = 125
£ = 275 mm = 10,82"
Dit is 1,34 maal de waarde die gemeten is. Een rekenfout? Een meetfout? Of is de formule toch net zo nauwkeurig als geclaimd wordt?
Formule 2:
£draad = πd × n = 3,14 × 32 × 125 = 12560 cm (125 m)
£spoel = 27,5 cm
L = 125602 / 27,5 = 5736472,7 nH = 5,74 mH en dat is ca 2× de gemeten waarde!
Formule 3:
Onze laatste hoop. Diameter/lengte = 320/275 = 1,16 en dat geeft een "K" van 0,66 in het nomogram. L wordt nu: 9,87 × 322 × 1252 × 0,66 ÷ 27,5 = 9,87 × 1024 × 15625 × 0,66 ÷ 27,5 = 3790080 nH = 3,79 mH en alweer een flinke afwijking t.o.v. de meting.
Maar... de uitkomst van formule 3 komt wel binnen 1% van die van formule 1 en dat geeft te denken. Is wel goed gemeten? De meter waarop ik de meting heb afgelezen heeft behalve de analoge schaal waarop de 2,8 mH is afgelezen ook een uitgang waarop de frequentie van de inwendige oscillator staat. Met de formule 1/f2 last zich de spoel veel nauwkeuriger meten. De frequentie was 17,59 kHz en dat geeft een L van 3,23 mH *). Al beter. Maar hoe groot is die spoel nu werkelijk? Ik verrichtte nog twee metingen en die liepen op nets uit. Deze metingen zijn allemaal gedaan op basis van een parallelkring. Zullen we eens een seriekring proberen?
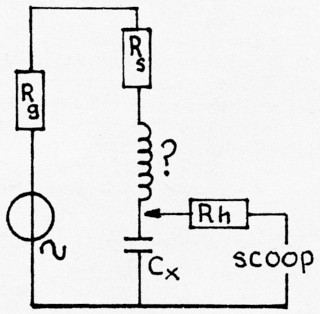
De resonantiefrequentie is uitsluitend afhankelijk van L en C en daarop hebben Rg, de inwendige weerstand van de generator (meetzender) en Rs, de verliezen in de spoel, geen invloed. Alleen Cx is gevaarlijk omdat daarop de scoop wordt aangesloten en die zou de waarde van Cx kunnen beïnvloeden. Door de hoogohmige weerstand Rh wordt die beïnvloeding voorkomen. Meestal voer ik een dergelijke meting zo uit dat ik de coaxkabel naar de scoop kan gebruiken als capaciteit. RG-58 heeft een capaciteit van 93,5 pF/m en de scoop een ingangscapaciteit van 40 pF... met anderhalve meter kabel zitten we dan op 140 + 40 = 180 pF.
Met Cx = 200 pF werd resonantie gevonden = maximum uitslag op de scoop, bij een frequentie van 140 kHz en dat ziet er gezond uit. Laten we de boel nog even narekenen.
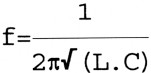
De formule is om te zetten naar: 2πF = 1 / √(L. C) of (2πf)2 = 1/(L.C) = (6,3 × 140k) = 8822 kk = 0,778 Mkk = 0,778 MM
L.C = 0,778 µµ en C = 200 pF = 200 µµ
L = 0,778 µµ / 200 µµ = 3,89 mH
De spoel gemaakt volgens formule 1 of formule 3 zou een spoel moeten opleveren van 3,79 mH. Meten we hem na dan blijkt hij 3,89 mH te zijn... een afwijking van 2,5%... fantastisch!
In de berekeningen worden m,k,M en p als getal gebruikt. Alhoewel ongebruikelijk is dit geheel legaal en voorkomt veel fouten met 'de nullen'. µ = mm. p = µµ. M = kk of 1/µ. Zie ook het begeleidend artikel "rekenen".
Nog een eenvoudige berekening voor spoelen:
n = lam : d
n = aantal windingen van de spoel
lam = lambda = golflengte in meters
d = diameter van de spoel in cm
Deze simpele regel gaat op zolang de bewikkelde lengte gelijk is aan de spoeldiameter en er bovendien een condensator van 82 pF wordt gebruikt voor de afstemming.
Werkt dit met onze grote langegolfspoel? Een spoel van 3,8 mH met 82 pF geeft een frequentie die op het nomogram net meer is af te lezen. Wat nu? 200pF is 2,44 maal 82 pF dus de frequentie gaat 42,44 = 1,56 maal omhoog met die kleinere 82pF. Dat wordt dus 1,56 x 140 kHz = 218 kHz zijnde een golflengte van 300 M : 218 k = 1,38 k. Lambda is dan 1380 meter.
Het aantal windingen zou dan moeten zijn: n = 1380/32 = 43 maar we hebben er echter 125 nodig om 3,79 mH te verkrijgen. Zullen we deze "formule" of vuistregel ook maar naar de prullenbak verwijzen!?
√(L.C)
Veel berekeningen kunnen sterk vereenvoudigd worden als we ons realiseren dat de frequentie uiteindelijk bepaald wordt door de "wortel uit L maal C". Als we met de frequentie van een bestaande kring, bijv. een MF-trafo een factor twee omhoog willen, dan moet het product van L maal C met een factor vier worden verkleind. Met 2 µH en 130 pF resoneert een kring op 10 MHz (nomogram). Verkleinen we of C of L met een factor 4 dan komen we op 20 MHz, dus met 0,5 µH en 135 pF of 2 µH en 33 pF.
Met een kern

Met een kern in de spoel kunnen we de zelfinductie verhogen. Het spoeltje op de foto, 30 wdg op een stukje plastic installatiebuis, heeft een zelfinductie van 8,5 µH zonder kern en met een staafje ferriet (van een MG-ferrietantenne) van 35 mm lengte en een diameter van 9 mm kan de zelfinductie worden verhoogd tot 33 µH, bijna een verviervoudiging. Men zegt dan ook dat de permeabiliteit van dit stukje ferriet gelijk is aan 4, µ = 4. De µ = 4 is gevonden door twee metingen te verrichten, eentje met en eentje zonder de kern. Voor ieder materiaal en voor iedere afmeting van de kern vinden we een andere Als we weten welke soort ferriet is gebruikt, maar dat staat er meestal niet op, dan kunnen we aan de hand van de data-sheets van de fabrikant de µ wel achterhalen. Dit is echter een ingewikkelde materie.
Ferriet is niet het enige materiaal om spoelkemen te maken, ook gesinterd ijzerpoeder komt in aanmerking. Beide materialen dient men niet boven de 'grens- of kritische frequentie' te gebruiken. De permeabiliteit neemt dan af en de verliezen gigantisch toe. IJzerpoeder kernen lenen zich beter voor oscillatoren, afgestemde kringen en hoge frequenties dan ferriet, een materiaal dat geschikter is om te gebruiken voor HF-transformatoren en breedband toepassingen... waaronder begrepen ontstoringsfilters. Bij permeabiliteits-afstemming - zoals in autoradio's - schuift men de kern mechanisch in en uit de spoel. Met de spoel op de foto kan men de zelfinductie op deze manier instellen tussen 8,5 en 33 µH. En over welk gebied kan men zo de resonantiefrequentie wijzigen? Als L met een factor 4 varieert dan doet het product van L.C dat ook en de √(L.C) met een factor 2.
Ringkernen
In principe wijkt een op een ringkern gewikkelde spoel net veel af van een gewone spoel. De kern is rondgebogen tot een ring waardoor het magnetische veld niet meer door de lucht behoeft te gaan. Dit heeft twee voordelen:
- Een spoel op een ringkern heeft een zeer klein strooiveld en pikt ook weinig tot geen storing van buiten op.
- Lucht is een slechte magnetische geleider en omdat er met een ringkern geen "weg door de lucht" meer is heerst er een grotere veldsterkte in de kern van een ringkern dan in een "gewone" spoel. De consequentie hiervan is dat er bij gebruik van een ringkern veel minder windingen nodig zijn dan bij een gewone spoel om dezelfde zelfinductie te realiseren.
Net als bij een gewone spoel neemt de zelfinductie toe met het aantal wikkelingen in het kwadraat. De volgende formule komt u in de meeste handboeken over ringkernen tegen:
![]()
Wilt u de waarde van de spoel "L" of het aantal windingen "n" dat voor die zelfinductie nodig is weten dan heeft u "M" nodig. M is een factor die afhankelijk is van de afmetingen en het gebruikte materiaal van de ringkern. M is een theoretische waarde die betrekking heeft op 100 (soms 1000) windingen en is bestemd om te kunnen rekenen. (Voor 1000 wdg wordt de formule: n = 1000 √{L/A£}.) Voor in het front-end van een 50 MHz transceiver had ik een stel spoelen nodig met een gering strooiveld om oscilleren door terugkoppeling te voorkomen. Gewenste spoel: L = 0,33 µH en de gekozen kern een T37/2 met A£ = 40. Het aantal windingen n = 100√(0,33 ÷ 40) = 100√0,00825 = 100 × 0,09 = 9 wdg. Na het wikkelen voldeed de spoel aan de gewenste specificaties. Merk weer op dat de draaddikte niet in de formule voorkomt.
Een paar jaar geleden kwam een medeamateur aan de deur met onder zijn arm een schoenendoos... een uit de hand gelopen QRP- bouwproject. Een van de weinige delen die het wel deed was de oscillator en die was uitgevoerd met een ring-kern. Een VFO met ringkern dat is vloeken in de kerk. De "deskundigen" zijn het er over eens dat met een ringkern geen stabiele oscillator gebouwd kan worden. Nadat ik eindeloos met C-tjes in de weer ben geweest is het verloop nu minder dan 10 Hz/24 uur op 80-meter. De kern was er eentje van Amidon, de T50/2. T=ijzerpoeder (FT=ferriet). 50 is de diameter = 0,50"(inch) en /2 is het materiaal dat het frequentiegebied mede bepaalt. In de documentatie van Amidon wordt voor deze ringkern een A£ = 4,9 aangegeven en bij het narekenen van deze spoel klopt de gegeven formule ook als een bus.
Er zijn er nog veel meer!
Een kern van ferriet is eerder verzadigd dan eentje van ijzerpoeder. Gebruik voor breedband-trafo's en baluns bij grote vermogens een grote kern!
| Type | Diam | A£ | Freq | Kleur/power |
|---|---|---|---|---|
| T68/1 | 17 | 115 | 0,2-10 | blauw |
| T37/2 | 8 | 40 | 3-50 | rood |
| T50/2 | 12,5 | 49 | 2-50 | rood |
| T68/2 | 17 | 57 | 1-30? | rood 35 W |
| T80/2 | 20 | 80 | 1-30 | rood 60 W |
| T106/2 | 27 | 135 | 1-30 | rood 100 W |
| T68/3 | 17 | 195 | 0,05-5 | grijs |
| T37/6 | 10 | 31 | 5-40 | geel |
| T50/6 | 12,5 | 40 | 3-40 | geel |
| T68/6 | 17 | 47 | 2-40 | geel |
| T37/10 | 10 | 25 | 20-150 | zwart |
| T50/10 | 12 | 30 | 10-100 | zwart |
| T37/12 | 10 | 15 | 30-400 | groen/wit |
| T50/17 | 12 | 18 | 25-300 | geel/blauw |
Afscherming
Het aantrekkelijke van ringkernen is dat het magnetische veld in de kern geconcentreerd blijft en dat die kern gesloten is, m.a.w. er hangt geen magnetisch veld rond de spoel dat kan inwerken op de bedrading van een schakeling of op een andere spoel. De onbedoelde magnetische koppeling kan allerlei ongewenste effecten geven zoals oscillaties en daar kunnen we last van hebben bij het gebruik van de z.g.n. "open spoelen" zoals die die we net gewikkeld hebben.
Aan deze last is wel iets te doen: afscherming. Afscherming wordt veelvuldig toegepast, veelal in de vorm van een blikken of aluminium huisje om de spoel. Zelden wordt de afschenning op deze manier goed toegepast, ook niet door bekende fabrikanten. We moeten er namelijk voor waken dat de afscherming geen kortgesloten winding om de spoel vormt. Om de spoel van foto 2, de spoel met het ferrietstaafje gewikkeld op een plastic buisje met een diameter van 16 mm, heb ik een afscherming aangebracht van blik. Vierkant 40 × 40 mm... dat is een royale afstand tot de spoel maar de oorspronkelijke hoge Q was volledig genfineerd. Met een blikschaar is vervolgens een opening van 2 mm, over de gehele lengte van de spoel, geknipt om de kortgesloten wikkeling op te heffen. Na deze operatie functioneerde de spoel weer goed en door de 2mm brede spleet ontsnapt geen of nauwelijks HF.
Een tweede voorbeeld. Een van mijn eerste bouwprojekten voor HF was een buizenzender met een uitgangsvermogen van een watt of twaalf. Het ding functioneerde best aardig todat ik er, om het netjes te maken, een fraai metalen kastje omheen maakte. Het vermogen liep terug tot ca. een watt waarbij het gemakkelijke afstemmen van de tankspoel ineens niet meer wilde. Deze zender slingert nu ergens rond in de shack en het is onwaarschijnlijk dat ik hem nog eens onder handen neem.
Een andere veelgebruikte manier van afschermen is het gebruik van een (blikken) doosje met kamertjes of afschermschotjes. De kans op een kortgesloten winding door de kast is zo wat kleiner maar kan optreden als het laatste dekseltje gesloten wordt. Het monteren van spoelen "staand" op de print kan problemen geven... de print of het aardvlak op de print kan gemakkelijk als kortgesloten winding gaan fungeren. Dus: oppassen met afschermschotjes en metalen behuizingen.
Het is ook lang niet altijd nodig om af te schermen. Wat kan het nut zijn van het afschermen of opbergen van een antennetuner in een metalen doos als de antenne die aan die doos zit bedoeld is om zoveel mogelijk RF-vermogen uit te stralen? Een plastic of houten omhulsel werkt veel be-ter en geeft ook bescherming tegen hoge spanningen. En als het perse metaal moet zijn... maak dan ergens een gleuf of breng een strook van isolatiemateriaal aan om de 'kortgesloten winding' die de kast gaat vormen te onderbreken. Er zijn in de amateurpraktijk meer voorbeelden te vinden van een schadelijke afscherming in een situatie waarin die afscherming helemaal niet nodig is. Probeer eens van die reflex af te komen om alles maar in te blikken. Vaak is dat nodig, maar lang niet altijd.
Er is nog veel meer over spoelen of alternatieven daarvoor te vertellen. Kijk nog maar eens terug naar de 'lechers' in CQ-PA augustus 2000.
*) Deze L-meter wordt beschreven in het boek "Fantasie & Zelfbouw" door PA3FFZ. Met de L-meter zijn ook ingeblikte spoelen met parallel-C's nauwkeurig te meten.
Bastiaan, PA3FFZ.