Rob's web

Home - Techniek - Electronica - Radiotechniek - Radio amateur bladen - Practical Wireless - External noise vs receiver sensitivity

External noise vs receiver sensitivity

All listeners to the h.f. bands know that external noise can sometimes cause even strong signals to become unreadable. For this reason, many textbooks on h.f. receivers contain a sentence to the effect that, the sensitivity of h.f. receivers need not be very good.

In spite of what the textbooks say, the signal to noise ratio sensitivity of modern receivers is becoming better and better. You only need to look at advertisements and reviews. Many amateurs must have asked themselves the question: When really is the sensitivity good enough and at what value is there no point in improving it anymore?

I found a few articles on this subject but none really gave me the answer, until I read the article by Gerald Stancey G3MCK(1).

This article addresses the point directly and is actually a very good one. My article is an extension and expansion of Gerald's thoughts and an attempt to arrive at some sort of answer.

No Theory

I'm not going through all the theory of noise, sensitivity, noise figure, noise factor, etc. This is given in all textbooks and well condensed in Gerald's article. I shall only give a few of his final formula here.

If the `noisiness' N_y, of a receiver is defined as: the signal to noise ratio at the input (S_i/N_i) divided by the signal to noise ratio at the output (S_o/N_o) of a receiver, it can be shown that

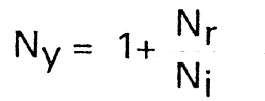
where:
N_y = noisiness of the receiver
N_i = noise at input of receiver (external noise)
N_r = noise added by receiver

If the lowest possible external noise is only the thermal noise at room temperature in a certain bandwidth, we can take this as standard (N_s). Then N_i = N_s. At this condition, the noisiness, N_y = N_Fa (the well-known noise factor) or noise figure N_Fi if expressed in dB. The relationship between the two is: N_Fi = 10log(N_Fa).

Thus we can see that

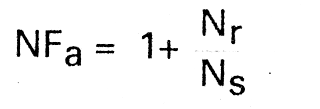
Now, say the noise input N_i is a factor N_e more than the standard N_s, then N_i = N_eN_s or N_i = N_e + N_s (when expressed in dB) Then

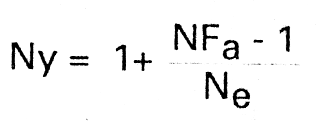
We now have thenoisiness, N_y, in terms of the noise Factor, N_Fa, and the external noise, N_e, above the noise standard, N_s.

An Example

Let's have an example. Say a receiver has a N_Fi = 16(dB), then N_Fa = 40. If on 21MHz the external noise is 20dB above the standard, eg. N_e = 100, then

S_o, if the minimum discernible signal (m.d.s.) is where S_o = N_o then S_i = N_yN_i = 1.39N_i or, S_i must be 1.43dB higher then N_i. If S_o/N_o must be 10dB then S_i must be 14.3dB above N_i. Or if S_i/N_i = 10dB, then S_o is only 8.57dB above N_o.

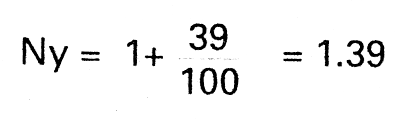
Calculations & Results

From the above theory we can now draw up a few tables and graphs to put the whole thing into perspective. In Table 1 the external h.f. spectrum. noise data is summarised. This data can be found in virtually every radio handbook.

The data in Table 1 is taken from the Radio Communications Handbook. In column 1 of the table are the different frequency bands. Column 2 is the different times of day conditions. Column 3 is the external noise N_i reaching the antenna in dBm (referred to one milliwatt).

Column 4 is the same data expressed in microvolts to give you a better feeling for the values. In modern transceivers S9 on the S-meter can represent anything between 20 to 50µV an the antenna.

Column 5 in the table is the external noise N_e (in dB) above the s tandard (-141dBm in this article, which is the thermal noise at room temperature in a 2100Hz bandwidth).

A rough plot of Ne against frequency is shown in Fig. 1. You can see the noise levels on the 1.8, 3.5 and 7MHz bands in stormy conditions really are quite high - as you all well know.

Now we come to Table 2 where column one contains different values of Ne. Column two has four different values of receiver sensitivity noise figure (N_Fi) in every Ne group. Column three has the same values in V.

Columns 4 and 5 are calculated values of S_i/N_i for m.d.s. (S_o = N_o), using the relevant values of N_e and N_Fi (converted to N_Fa). In columns 1, 2 and 6 are the value of S_o/N_o (in dB) to give an input value of S_i/N_i = 10dB for the different Ne and N_Fi values.

If the above S_ounds complicated, it will be clearer after looking at Fig. 2, a plot of the figures in Table 2. The plot is column one against column six for the different values in column two. Putting the explanation in full: Fig. 2 is a plot of the external noise Ne against S_o/N_o (if S_i/N_i = 10) for different values of receiver sensitivity N_Fi.

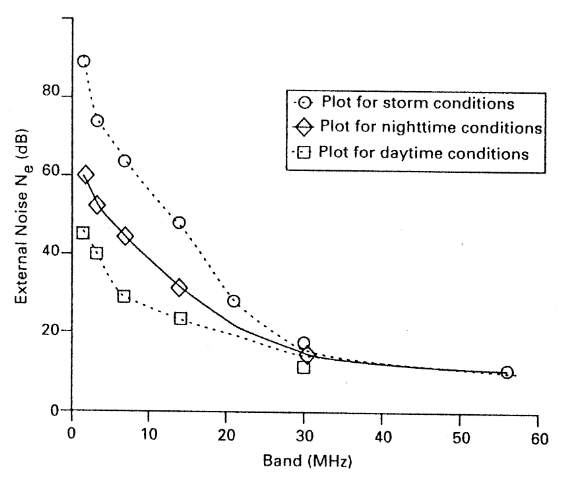
Fig. 1: This graph plots the external noise above a standard level for over the various bands.

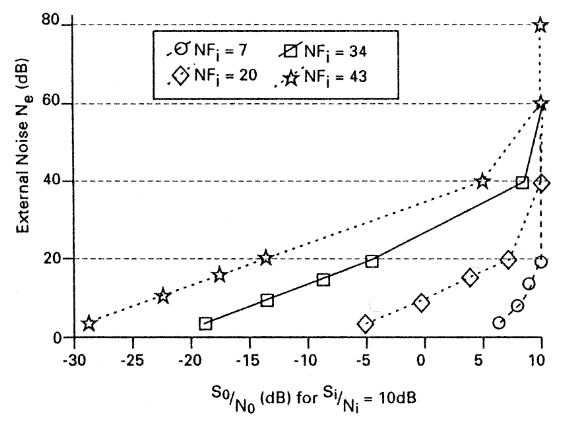
Fig. 2: This graph shows the external noise above a standard against S_o/N_o (when Si/Ni=10) for differing values of receiver sensitivity (N_Fi).

Table 1: Showing external noise for various frequency bands. The right hand column (N_e) is shown as dB above above the standard (N_s) {N_e=N_i-N_s or N_i-(-141 dB)}.

Band	Condition	noise		noise above
MHz		dBm	µV	standard
1.8	Storm	-51	630	90
	Night	-81	20	60
	Day	-96	3.5	45
3.5	Storm	-66	112	75
	Night	-88	8.9	53
	Day	-101	2	40
7	Storm	-76	35	65
	Night	-96	3.5	45
	Day	-111	0.63	30
14	Storm	-96	3.5	45
	Night	-108	0.89	33
	Day	-116	0.35	25
21	Storm	-111	0.63	30
	Night	-116	0.35	25
	day	-121	0.2	20
28	Storm	-126	0.11	15
	Night	-126	0.11	15
	Day	-126	0.11	15
56	Storm	-131	0.063	10
	Night	-131	0.063	10
	Day	-131	0.063	10

Another example

As an example: Say on 7MHz during daytime the figure for N_e = 30 (from Fig. 1) and you have a receiver with a poor N_Fi = 34dB (lµV). You can see from Fig. 2 that you will get S_o/N_o = 4.4dB for an input of S_i/N_i = 10dB. It is from Fig. 2 that we will try to answer the question posed at the start of the article.

Some conclusions

To arrive at some conclusion we must move from radio science to human physiology, which differ from individual to individual. In physiology textbooks one reads that the smallest difference in sound (at say 1000Hz) that the human ear can detect is 1dB(3).

The figures quoted seemed very low in value S_o, in the interests of science, I did a few rough experiments with two of my children. Using an amplified audio signal generator, and an a.c. digital voltmeter I let them hear pure tones through headphones. Sure enough, all the values were between 1 and 2dB except at very low sound levels where it rose to 3 or 4dB.

Returning to Fig. 2, if the perfect receiver gives S_o/N_o = 10dB for S_i/N_i = 10dB and, if one can detect a 1dB difference, then you should be able to detect a difference at S_o/N_o = 9dB and lower.

So, if we draw a vertical line at S_o/N_o = 9dB in Figure 2, then at all conditions left of this line we will be able to detect a deterioration in readability. Let's take a few examples.

1. During daytime on 3.5MHz, the N_e = 40dB (from Fig. 1). Entering N_e = 40 in Fig. 2 we see that it cuts the vertical line where S_o/N_o = 9dB at N_Fi = 34dB (1µV). S_o, any better sensitivity won't help you at 3.5MHz.
2. At 28MHz it can be seen from Fig. 1 that N_e is about 15dB. Entering N_e = 15dB in Fig. 2, we see that it cuts the S_o/N_o = 9dB line at a point between N_Fi = 20 and N_Fi = 7. But I estimate the value, to be probably at N_Fi = 9dB. So, on 28MHz it is worthwhile to have a receiver or pre-amp with this lower noise figure.
3. Let's take everybody's favourite band (well it's mine anyway) 14MHz. During day time N_e = 25dB, giving an N_Fi of approximately 18dB. During night time N_e = 33, which gives an N_Fi of approximately 24dB. During stormy conditions, N_e = 45 giving a N_Fi of approximately 39dB. All of the above interpolated at the S_o/N_o = 9dB line.
4. If you build small receivers at home, then design it for the N_Fi values in Table 3 for good readability, taken from daytime Ne values.

There is another question that can be asked. If you don't really need S_o/N_o = 10 or 9dB to read a signal, what is the lowest value of S_o/N_o that is still readable. There are experienced c.w. operators can read a signal below the noise level. On s.s.b. mode if someone at the other end of the link is reading numbers slowly it can also be read just below the noise level(4).

Say, for arguments sake, the lowest that can be read is S_o/N_o = 0dB, that is the m.d.s. level. N_ow we can determine the approximate least sensitivity which is needed on the different bands if S_i/N_i = 10dB. From Fig. 1, again get the daytime N_e values for the different bands, enter this at the left hand side of Fig. 2 and read the approximate values of N_Fi at the S_o/N_o = 0dB vertical line. We get the following:

1.8MHz	NFi = 60dB
3.5MHz	NFi = 50dB
7MHz	NFi = 38dB
14MHz	NFi = 34dB
21MHz	NFi = 28dB
28MHz	NFi = 23dB
56MHz	NFi = 21dB

The above values of N_Fi are for S_o/N_o = 0dB if S_i/N_i = 10dB

We can N_ow determine N_Fi for many S_o/N_o values, or we can take a certain N_Fi value from Table 2 and determine what S_i/N_i must be for S_o/N_o = 0 on every band. An interesting S_o/N_o case is where S_i/N_i =1dB (S_i/N_i = ratio 1.26). At this point S_o/N_o is 1dB less than S_i/N_i. If we follow the arguments through we see that in this case the N_Fi values are the same as that given in Table 3. S_o, it seems as if the N_Fi values in Table 3 is the lowest that we must aim for on the different bands.

I must emphasise that my conclusions will differ from person to person. The human ear/brain is a remarkable instrument with surprising filtering properties. S_o much S_o, that it's nearly impossible to describe in exact terms.

Table 2: External noise and signal to noise ratios for differing receiver sensitivities.

External noise above standard Ne = Ni - Ns	Receiver sensitivity		Si/Ni for m.d.s.		So/No for Si/Ni = 10dB
	NFi	µV	Ratio (Ny)	dB
80dB	7	0.046	1	0	10
	20	0.2	1	0	10
	34	1.0	1	0	10
	43	3.0	1.0002	0.0009	9.9991
60dB	7	0.046	1	0	10
	20	0.20	1.0001	0.0004	9.9996
	34	1.0	1.0025	0.0018	9.9892
	43	3.0	1.0200	0.0860	9.9140
40dB	7	0.046	1.0004	0.0017	9.9983
	20	0.20	1.0099	0.0428	9.9572
	34	1.0	1.2511	0.9729	9.0271
	43	3.0	2.9952	4.7643	5.2357
20dB	7	0.046	1.0400	0.1703	9.8297
	20	0.20	1.9900	2.9885	7.0115
	34	1.0	26.11	14.168	-4.168
	43	3.0	200.5	23.021	-13.021
15dB	7	0.046	1.1266	0.5177	9.4823
	20	0.20	4.1329	6.1625	3.8375
	34	1.0	80.46	19.056	-9.056
	43	3.0	832.4	28.010	-18.010
10dB	7	0.046	1.4000	1.4612	8.5388
	20	0.20	10.90	10.374	0.3740
	34	1.0	252.1	24.016	-14.016
	43	3.0	1996	33.002	-23.002
5dB	7	0.046	2.2658	3.5522	6.4478
	20	0.20	32.33	15.096	-5.096
	34	1.0	795.6	29.007	-19.007
	43	3.0	6315	38.004	-28.004

Table 3: Suggested minimum receiver noise figures for the various frequency bands (see the text for more details).

Band (MHz)	Ne (dB)	NFi (dB)
1.8	45	40
3.7	40	34
7	30	22
14	25	18
21	20	13
28	15	9
56	10	6

References

1. Stancey Gerald G3MCK, 'noise in h.f. receivers', Practical Wireless, August 1984.
2. Radio Society of Great Britain, Radio Communication Handbook, Volumes 1 & 2.
3. Katz J., Handbook of Clinical Audiology, 1985
4. Ainsworth W., 'Recognising speech in noise'. Electronics Today International, April 1989.

ZS6UP