Note on inductance calculation
Designing coils having a fixed winding pitch.
In designing air-core coils for a desired in-ductaicc and where a table or chart (or the ARRL Lightning Calculator - Ed.) are not readily available, the equation
![]()
is used, where L is the inductance in micro-henrys, a is the mean diameter of the coil in inches, b is the length of the winding in inches, c is the radial depth or thickness of the winding and n is the number of turns. In the case of single-layer coils, 10c may be neglected so that the equation becomes
![]()
This is the form of the equation that will be discussed here.
Insofar as the coil diameter and the desired inductance are known, the equation usually is rearranged to solve for the number of turns of wire directly and a value for b is assigned that will suit the design. Thus when the number of turns has been determined from the equation, it is simply a matter of spacing these turns equally in the length b as chosen. For this purpose the equation is written
![]()
or
![]()
The number of turns solved for must be spaced out in the length already assigned by the value b, and very often this spacing is an odd value that is difficult to accomplish. Furthermore, the formula cannot be used for a winding with a desired turn spacing or "pitch," nor does it provide a precise solution for close-wound coils, whose "pitch" is the number of turns per inch listed in the wire tables for the particular size and type of wire being used. However, a precise solution for any "pitch" is easily found as follows:
Every coil has a certain number of turns per inch, or "pitch," whether it be the value from the wire tables or any other spacing that may be desired. Hence, the length b of any coil can be stated in terms of the total number of turns divided by the number of turns per inch, or "pitch," or, we can say b = n/P. Then the equation (3) becomes
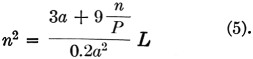
By a little algebraic manipulation this can be put in the form
![]()
This is an equation in the quadratic form x2 - ux = v, the solution for which is
![]()
If the coefficient of n in parentheses in equation (6) is substituted for u and the right-hand term of equation (6) is substituted for v, the equation becomes
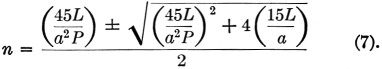
At first glance, this appears to be quite formidable, but since L, a and P are known, it is readily apparent that the values shown in parentheses will resolve into single terms, thereby making the solution quite simple.
If the terms shown in parentheses in equation (7) are tabulated, their values become constants for the particular size of wire and diameter of coil form being used. A tabulation of such constants for ½ inch diameter forms is shown in Table 1.
| Gauge | P | |||
|---|---|---|---|---|
| 18 | 23.6 | 7.63 | 58.2 | 120 |
| 20 | 29.4 | 6.12 | 37.5 | 120 |
| 24 | 46.3 | 3.89 | 15.1 | 120 |
| 28 | 72.7 | 2.48 | 6.13 | 120 |
| 32 | 113 | 1.59 | 2.54 | 120 |
The value of P in the above table is for enameled wire as listed in the wire tables.
To illustrate this simplification, assume that a coil of No. 28 enameled wire is to be close-wound on a ½ inch diameter form. Equation (7) then would be
![]()
and the only remaining variable would be the value of inductance desired.
Theodore Elliott.