Measuring SSB/CW receiver sensitivity
The ability of a communications receiver to copy very weak radio signals is one of its most important attributes. Here's how to quantify this particular fundamental specification of basic receiver performance.
Sensitivity is an important communications receiver specification. Intuition suggests that this is the receiver's ability to distinguish a weak signal (produced by a lab signal generator having a specified temperature and output impedance) from background noise. When the receiver is connected to an antenna, the system sensitivity may be much different, but the spec-sheet sensitivity value is still a useful baseline for designing a receiving system. This article examines the more precise meanings of sensitivity and describes some methods of measuring it. It also describes in detail a simple home-brew instrument - a true-RMS-to-dc converter - which is especially useful for making accurate sensitivity measurements. The instrument can also be used for other valuable measurements.
Sensitivity, noise figure and noise power bandwidth
Excess noise power (noise in "excess" of thermal noise power) is generated at various locations within a receiver. This power appears at the receiver output with a magnitude and power-spectrum shape which is determined by the various band-pass filters (RF, IF and AF) through which it passes, by the magnitudes of these excess noise sources, and by the gain following each excess noise source. The output also contains a thermal noise power component which is a basic natural phenomenon, generated all along the receiver signal path and also by the output impedance of the signal generator connected to the receiver antenna jack. These sources of thermal noise are also processed in various ways and the spectrum of thermal noise at the receiver output can be quite different from that of the excess noise.
At the receiver output, the total noise power is the sum of thermal noise power and excess noise power. The noise factor of the receiver is simply the ratio of the total noise power to the thermal noise power (if we somehow know the value of the thermal noise power). The receiver noise figure is 10 times the base 10 logarithm of its noise factor and is expressed in decibels (dB). The measurement of noise figure will be discussed later.
Noise figure is a widely accepted figure of merit for a receiver. But we also need to know the receiver sensitivity - the value of the weakest signal that can be copied correctly. Historically, for conventional SSB/CW receivers this signal is quite often assumed to be such that the sum of signal and total noise is 10 dB greater than the noise alone. This means that the signal is 9.54 dB greater than the noise.(1)
The noise level is proportional to the product of the receiver's noise factor and bandwidth. This implies that the best sensitivity is achieved when the bandwidth is no greater than that required for the signal (for example, 2.4 kHz for SSB and 150 to 500 Hz for CW). It also implies that a receiver which is equipped with switchable IF filters of equal insertion loss is more sensitive in narrow-band communication modes. A properly designed receiver will copy significantly weaker CW signals than SSB signals, even when antenna noise is very small.
The noise power bandwidth, exemplified in Fig 1 , is defined as the width of a fictitious perfectly rectangular spectrum that contains all of the significant noise power in the receiver output spectrum. The output spectrum itself may have a wide variety of shapes, as mentioned above. The flat top of this fictitious response can be viewed as an averaging process for the noise spectral density. Later discussion shows a simple method (subject to certain limitations) for measuring the approximate noise bandwidth of a receiver.
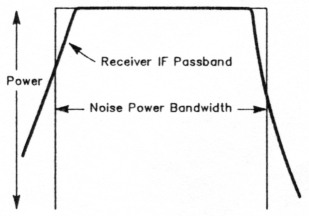
Fig 1 - A receiver's noise power bandwidth is defined as the width of a fictitious perfectly rectangular spectrum that contains all of the significant noise power in the receiver output spectrum. The output spectrum itself may take a wide variety of shapes.
Noise figure, noise bandwidth and 10-dB sensitivity for SSB/CW are neatly tied together by the following formula:
![]()
where S is the 10-dB sensitivity (dBm), -174 is available thermal noise power density (dBm in 1.0 Hz at room temperature), 9.54 is signal-to-noise ratio (dB), NF is noise figure (dB) and BW is noise power bandwidth (Hz). To get S in terms of voltage, use the formula
![]()
where E is the open-circuit voltage (called "hard" signal level) from a 50-ohm signal generator (twice the reading indicated on the generator's output meter with the generator operating into a 50-ohm load(2)) and S is in decibels relative to a milliwatt (dBm). An exception to the validity of Eq 1 will be discussed later.
Consider receiver intermodulation (IM) distortion caused by two or more strong CW signals on nearby frequencies. As bandwidth is reduced and sensitivity is thereby increased (S becomes smaller) these IM products become much more noticeable (they peek above the noise level). This is a very common effect in CW receivers that have poor IM performance. It is especially noticeable in a CW contest where band occupancy is very high. When the CW interferers are simultaneously "key down," a momentary beep is heard in the receiver. I have found myself actually trying to copy these phantom signals!
Signal, noise and sensitivity measurements
The instantaneous voltage amplitude of the random noise output of the SSB/CW receiver which uses a product detector has the Gaussian probability density (the familiar bell-shaped curve). If this noise voltage has a certain RMS value (the same as its standard deviation, or sigma [Σ]), its peak value exceeds four times its RMS value only about 0.01% of the time. The crest factor is the ratio of this peak value to the RMS, in this case 4. A voltmeter that measures the RMS value to this accuracy must not compress these occasional peaks, so its crest-factor rating must be at least 4. Also, the voltmeter's 3-dB bandwidth should be at least 20 times the width of the spectrum being measured to keep the error within 0.2 dB. (This assumes a simple one-pole frequency response.)
During receiver sensitivity measurements the receiver output also contains a sine wave test signal. We want to measure the ratio (noise + sine wave) / noise. To do this accurately, we should use a true RMS voltmeter. A conventional rectifier-type ac voltmeter which performs an averaging operation on the rectified voltage and displays the result on a scale calibrated for the RMS value of a sine wave does not indicate the correct RMS value of noise. The rule is that the RMS value of noise is 1.05 dB greater than the value indicated on a conventional averaging ac voltmeter. Although it's possible to use such a meter and make this simple correction, it is often neglected. The indicated RMS value of sine wave plus noise is also slightly inaccurate.
A true-RMS voltmeter is the correct instrument to use. The meter should have sufficient damping so that its noise reading can be visually averaged easily. Commercial digital multimeters tend to be unsuitable in this respect. High-pass filtering to remove receiver-noise components below 1 Hz or so is also desirable.
The proper place to connect the voltmeter is in the audio section - after all of the audio selectivity circuits, but ahead of the loudspeaker. (Variations in speaker impedance with frequency may introduce substantial measurement errors.) It's best to use a resistor as a temporary load, with a quick-connect/disconnect headphone or speaker hookup to allow audio monitoring by ear. Many receivers have a 500-ohm phone-patch output jack; this can serve as a test point if loaded with a 500-ohm resistor. It is informative to measure sensitivity before and after the receiver's audio filtering (if any), to see the difference. Be careful not to let hum and/or BFO energy contaminate your measurements.
It's very important that the receiver signal path be linear, with no compression. This invariably means that the AGC must be turned off. The signal path, without AGC, must be linear over the full peak-topeak range of signal plus noise, with RF gain at maximum. Suppose the noise has a reference RMS value of 1.0 with a crest factor of 4. Added to that is a sine wave whose RMS is 9.54 dB greater than 1.0. The peak-to-peak voltage swing is then 16.48 times as great as the RMS noise.
You can verify linearity with a simple test. Increase the test signal by 2 dB. The RMS voltmeter indication should increase very nearly 2 dB; if it doesn't, there is compression in the signal path. This 2-dB margin is called headroom.
If compression occurs, it's probably happening in the receiver's last IF stage. All is not lost if you run into last-IF-stage compression, because the gain of a receiver's last IF stage can almost always be temporarily reduced as much as 10 dB without significantly affecting the receiver sensitivity. This must be done by a means that does not disturb other stages or IF-transformer tuning. The linearization method you use will probably have to be worked out on a case-by-case basis. Receiver linearity should be verified at each test frequency.
An additional test that tells something about the receiver's dynamics is to connect a variable dc supply to the AGC bus, reduce the receiver's gain in 5-dB steps and measure sensitivity at each step. You can use the receiver's RF gain control to do this if it controls gain in the same manner. If the receiver's gain and AGC are properly distributed, sensitivity will fall off gradually for the first 20 dB or so and more rapidly thereafter.
Measuring receiver noise performance
The following procedures assume the use of the RMS-to-dc converter described in the sidebar. You can use some other true-RMS voltmeter as long as it adheres to the specifications described above. Instead of changing attenuation settings as called for in the instructions for using the converter, you could read the necessary 3- and 10-dB level shifts directly on your meter's decibel scale. But the 3-dB and 10-dB switch positions in the RMS-to-dc converter completely eliminate any meter calibration errors. This is recognized as a superior measurement technique.
All of the procedures assume that the receiver BFO is offset from the IF passband in the normal SSB/CW manner. They also assume (for reasons to be explained) that the receiver's IF passband ripple (amplitude peaks or valleys) is less than one dB or so. If these assumptions are true, the measurement accuracy obtained should be sufficient for most purposes.
Measuring noise level. This test also measures minimum discernible signal (MDS). Connect a signal generator to the receiver. Verify the receiver's linearity with its AGC off. Connect the converter's input to the receiver output via a 10: 1 probe. Turn the signal generator's output off. Set ATTENUATOR (S2) to 0 dB and adjust LEVEL so that the converter's dc output with noise only is 200 mV. Set ATTENUATOR to 3 dB. Turn on the signal generator RF and increase its level until the converter output is again 200 mV. The RF level in dBm at which this occurs is referred to as the receiver's noise level or noise floor and is equal to the total receiver noise power (thermal plus excess). If the receiver is connected to a noisy antenna or a noise generator, the excess noise power of these sources can be measured using the signal generator. From the total noise power (convert dBm to watts), subtract the receiver noise (also watts) and convert the difference back to dBm. The value thus measured is correct for the particular receiver noise bandwidth in use. The RMS-to-dc converter is the correct instrument to use when making these measurements.
Be sure to make this measurement at the audio frequency that corresponds to signals near the center of the receiver's IF/AF passband, and use this frequency consistently throughout your measurements. An audio frequency counter is recommended.
This single-measurement procedure assumes that the receiver's passband is free of sharp peaks or dips. If one or both of these are present, a single noise-floor measurement may give results that are misleadingly high or low depending on whether you measure at a passband dip or peak, respectively (see Fig 2). The measured noise floor would be incorrect, for example, for an SSB signal that occupies 2.5 kHz. You can confirm the presence of peaks or dips by slowly tuning the signal generator through the receiver passband and watching for them in the converter output. You can reduce their effect by measuring at several test frequencies (the highest peak, the lowest dip and some points between) and averaging the results.
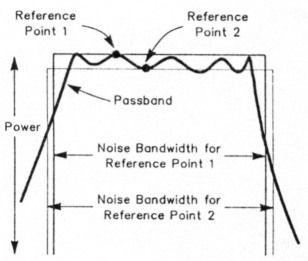
Fig 2 - A single noise-floor measurement may give misleading results if significant passband amplitude variation is present. Averaging readings taken at several spots throughout the passband can reduce this error. The value of noise power bandwidth is influenced by the choice of reference frequency.
A true-RMS-to-DC converter
The main text mentions that conventional rectifying/averaging ac voltmeters can give misleading indications when measuring receiver noise. Accurate dc voltmeters are inexpensive and easy to come by, however. Fig A shows a circuit that turns a dc voltmeter into a trueRMS voltmeter. The circuit uses an Analog Devices AD636JH RMS-to-dc converter IC which costs under $20 per unit in small quantities. It delivers a positive-going dc which is equal to the RMS input with better than 1% accuracy for input signals with a crest factor of 4 or less. The device is laser-trimmed for optimum accuracy at an input signal of 200 millivolts RMS (I use it in that manner for most measurements) but at 50 mV and 500 mV its accuracy degrades very little. And its frequency response is more than adequate for SSB/CW receiver audio measurements.
The converter has three input modes, selectable via Si, INPUT. A 10:1 oscilloscope probe which has a 10-megohm input impedance shunted by 12 pF (Tektronix P6109 In my case) can be dc coupled (DC), or ac coupled (AC) to U1A via C1. Si's third position, so, selects an ac-coupled low-impedance mode. R1 sets its impedance; I used 49.9 ohms to properly load my function generator. Test-select R3 so that the probe attenuation ratio is exactly 10.0 to 1.0. This assures that levels connected directly to J1 (without a probe) can be accurately measured without readjusting R4 (LEVEL). This means that 20.0 mV without the probe equates to 200 mV with the probe - a useful feature.
R4 adjusts U3's drive to 200 mV. R5 establishes this control's lower limit. If you cannot turn the level down far enough with the R4, reduce the signal applied to the Input probe. We don't want to overdrive U1A.
U2, an Analog Devices AD847JN wideband op amp, is set for a gain of about 10.5. This makes up for probe attenuation, with a little gain to spare. It is a bipolar device, so R6 is nearly equal to the parallel combination of R7 and R8. Set R9, NULL 1, to zero U2's output with zero signal present at J1. S2, ATTENUATOR, selects 0, 3 or 10-dB positions. These are set by R10, 3-dB ADJUST, and Rl 1, 10-dB ADJUST. More about this later.
With the input at pin 4 of U3 at zero, adjust R14, NULL 2, for zero output at our. C7 heavily damps U3's output response so that a DMM switched to its 200 mV dc scale can be used as an indicator across the our terminals with very little flickering of the reading.
U4 buffers the output of U3 and protects it from the outside world.
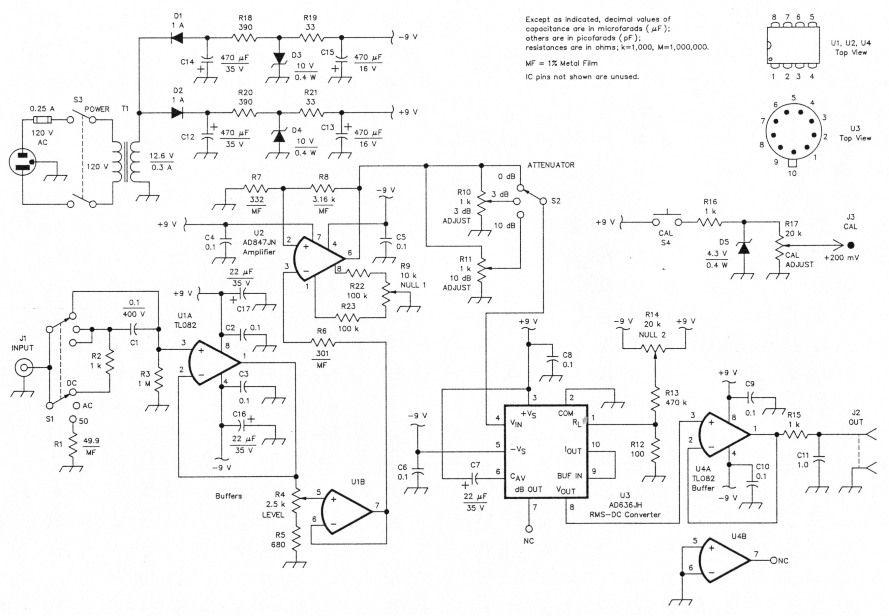
Fig A - Used in conjunction with a DMM capable of displaying 200 mV full-scale, this RMS-to-dc converter outputs as dc the true RMS value of input signals with a crest factor of 4 or less. All of its resistors are 1/4 watt, 5%-tolerance units unless indicated otherwise. PC-board templates for the converter and power-supply circuits are available from ARRL; see Note 3 of the main text. The Analog Devices ICs (U2 and U3) are available from a number of suppliers, including (among the suppliers listed in Table 42 of the 1992 ARRL Handbook's Chapter 35) Ocean State Electronics and Allied Electronics. Other Handbook-listed firms may carry them as well.
| D1, D2 | 1 A, 50 PIV (1N4001 or equivalent). |
| D3, D4 | 10-V, 0.4-W Zener diode (1N758 or equivalent). |
| D5 | 4.3-V, 0.4-W Zener diode (1N749A or equivalent). |
| R3 | Test select as described in the text. |
| R10, R11 | 15-turn potentiometer. |
| U1, U4 | TL082 dual op amp. |
| U2 | Analog Devices AD847JN op amp. |
| U3 | Analog Devices AD636JH RMS-to-dc converter. |
A front-panel test point, J3 (CAL), supplies a 200-mV dc calibration voltage as determined by R17, CAL ADJUST. Connect a DMM to the test point and adjust R17 for 200 mV at the test point. Next, connect the probe to cAL and adjust R4 for 200 mV across the OUT binding posts. R4 should then be at a little less than maximum. Once this is done, the 200-mV scale of a DMM across OUT will indicate the RMS value of applied noise or sine wave, or noise-plussine-wave, energy applied to J1. Finally, adjust the -3-dB and -10-dB pots, R10 and R11, for an output of 141 mV and 63.2 mV, respectively.
I recommend powering the converter from the ac-operated supply shown in Fig A. Batteries can power the circuit, but an ac supply eliminates the small but annoying calibration changes encountered with battery aging.
I constructed my version of the converter inside a chassis with a bottom cover and rubber feet. The adjustment pots are accessible from the rear. The converter power supply is on a separate PC board to keep ripple current off the converter ground plane. A three-wire line cord is used. - W0IYH

The RMS-to-dc converter and power supply fit into a 3 x 91/2 x 5-inch (HWD) chassis. A DMM connects to the converter via the our binding posts. (W0IYH photos)

Separate circuit boards carry the converter circuitry proper and power supply (right, on the chassis sidewall). Ground-plane construction would also suffice.
With the exception of these effects, which we assume will be minor in well-designed communications receivers, the accuracy of the measurement depends almost entirely on the accuracies of three factors: the RF generator's output level calibration, the converter's 3-dB attenuation and the RMS-to-dc conversion.
Measuring 10-dB sensitivity. Instead of using the ATTENUATOR 3 dB position as in Part 1, use the 10 dB position (the receiver AGC must be off). As in the previous section, error can result if the passband is not reasonably flat.
Measuring noise power bandwidth. The validity of the method to be described requires that the shape of the noise spectrum at the receiver output be very nearly the same as the shape of the signal selectivity, which may consist of several filters in cascade. In other words, all of the significant noise must be generated ahead of the signal selectivity, and the noise bandwidth of the receiver must be virtually the same as the noise bandwidth of the signal selectivity. If this is not true, a more complicated method is needed: Measure the baseband noise spectral density directly, using an audio spectrum analyzer. A well-designed SSB receiver has no problem in this respect, but some narrowband CW receivers may require special attention. In such receivers, wideband IF noise generated after the CW filter is quite often a problem. This is a direct result of the modern trend to minimize "front end" gain in order to maximize dynamic range.
A particular audio frequency must serve as a reference frequency for the set of measurements necessary to calculate noise power bandwidth. As we'll see later, it's important to use the same reference audio frequency that was used to measure sensitivity. With the receiver producing a beat note at this reference frequency, adjust the signal generator for 200 mV dc out of the RMS-to-dc converter. Record this signal generator reference level. Tune either the receiver or the signal generator in equal steps, 50 Hz for SSB or 20 Hz for CW, from low audio frequency to high frequency (this is important). At each frequency step, adjust the RF generator output to return the converter output to 200 mV.
The next step requires a computer running the available BASIC program to process the test data.3 Enter the RF signal generator levels (dBm, in frequency order), and the reference level, into the program. The program computes the noise power bandwidth that is correct for the reference frequency and the existing selectivity. In modern receivers with steep filter slopes, it's usually sufficient to take measurements down to 20 dB below the reference.
Calculating noise figure. Once you know the receiver's 10-dB sensitivity and noise bandwidth (both measured using the same audio reference frequency), you can calculate noise figure by rearranging Eq 1 as follows:
![]()
A home-brew noise generator(4) can also be used to find NF. Using the procedure described in measuring noise level, calibrate the noise generator by comparing its excess noise power output (within the receiver bandwidth),with the signal generator, using the converter. Then apply the "Y Method."(5)(6)
Conclusions about receiver noise
If wideband noise is generated after the receiver's SSB/CW filters, the receiver's full sensitivity may not be achieved if the post-filter noise amplitude is comparable to that of the composite noise from the antenna and the receiver front end. If prefilter noise, including antenna noise, dominates as it should, switching in a narrower filter will increase the measured sensitivity (lower the receiver noise floor). If postfilter noise is significant, reducing SSB/CW filter bandwidth will not provide the expected improvement in sensitivity. This problem is real because, as any HF DXer knows, at certain times, frequencies and beam headings, antenna noise becomes quite small and very weak signals are present. This is when maximum sensitivity is appreciated, and when wideband IF noise can be a problem.
If a receiver suffers from significant wideband IF noise, an audio "cleanup" bandpass filter is a simple way to improve it. Its bandwidth should be slightly wider than that of the IF filter in use. Unlike single-signal IF filtering, which rejects both signals and noise on "the other side of zero beat" or opposite sideband, an AF cleanup filter passes demodulated wideband IF noise from frequencies on both sides of the receiver BFO. An image-reducing product detector - implementable by means of BFO/AF quadrature phasing - is a better solution. The preferred approach, however, is to use a second "downstream" or "tail-end" narrow IF filter to achieve the desired noise bandwidth. Equations 1 and 3 will be rigorously valid if either of these single-sideband noise-reduction techniques is properly implemented.
Finally, if a receiver has considerable wideband noise after its SSB/CW filtering, its noise figure will increase as filter bandwidth is reduced. An easy way to see this is that if a noise generator is used to measure noise figure, it must now be cranked up higher to make the noise through the narrower filter equal to the constant value of wideband IF noise. An equivalent statement is that Friis's noise factor formula(7) for cascaded networks must now include the various bandwidth factors, usually ignored in systems where this special problem does not apply.
Notes
- Current practice often substitutes for sensitivity the term minimum discernible signal (MDS). MDS, defined as the signal level that is equal to the noise level in a specified bandwidth, equates to a 3-dB signal-plus-noise to noise ratio. MDS characterized in this way serves as the basis for the receiver dynamic testing done in the ARRL Lab. The 10-dB sensitivity specification is also commonly used in industry and government. - Ed.
- A signal generator with an internal impedance of 50 ohms can be thought of as a zero-impedance signal source in series with a 50-ohm resistor. The generator's output meter indicates the voltage that would appear across a 50-ohm output load. It follows, therefore, that the generator's open-circuit output voltage is twice that indicated on the output meter. - Ed.
- A printout of this BASIC program, NOISEBW, and PC-board templates and component-placement overlays for the RMS-to-dc converter described in this article, are available free of charge from the Technical Department Secretary, ARRL, 225 Main St, Newington, CT 06111. Send a business-sized SASE with your request for the SABIN RECEIVER SENSITIVITY TEMPLATE PACKAGE. NOISEBW can also be downloaded as the file NOISEBW.BAS from the ARRL BBS at 203-665-0090.
- D. DeMaw and W. Hayward, Solid-State Design for the Radio Amateur (Newington: ARRL, 1977), p 167.
- C. Hutchinson and J. Kleinman, eds, The ARRL Handbook for Radio Amateurs, 1992 ed (Newington: ARRL, 1991), p 12-3.
- W. Hayward, Introduction to Radio Frequency Design (Englewood Cliffs, NJ: Prentice-Halt, 1982), p 208.
- H. Goldberg, "Some Notes on Noise Figures," Proceedings of the IRE, Oct 1948, pp 1205-1214.
W0IYH, William E. Sabin.