Wirkungsweise und optimale Dimensionierung von Yagi-Antennen
Nach einem Vortrag auf der UKW-Tagung Weinheim 1976
Yagi-Antennen sind im VHF- und UHF-Funk weitverbreitet, da sie mit geringem Aufwand ansehnliche Gewinne erlauben. Die Zahl der Enttäuschungen mit nachgebauten, aber auch mit gekauften "Yagis" ist jedoch groß. Diese Arbeit soll helfen, Fehler und falsche Erwartungen zu vermeiden und zum allgemeinen Verständnis beitragen.
1. Homogene Yagi-Antennen
Die von H. Yagi erstmals 1928 beschriebene Antenne(1) wies zwar schon alle Merkmale heute gebräuchlicher (Lang-) Yagi-Antennen auf, aber ihre Wirkungsweise wurde erst viel später ganz verstanden. Eine der besten Arbeiten darüber wurde 1959 von Ehrenspeck und Pöhler veröffentlicht(2); sie lieferten auch Meßwerte von erstaunlicher Präzision. Ehrenspeck und Pöhler zeigten experimentell, daß sich längs einer Yagi-Struktur eine Welle mit verminderter Phasengeschwindigkeit ausbreitet, die am offenen Ende wie aus einem Rohr austritt. Dabei verhält sich die Direktor-Kette wie ein künstliches Dielektrikum, so daß eine nahe Analogie zu den dielektrischen Stiel- und Rohrstrahlern, sowie den Leitscheibenantennen besteht(3).
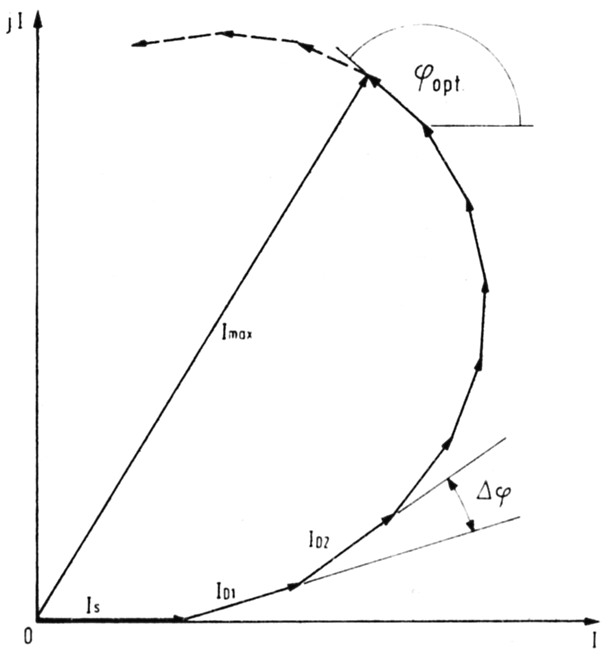
Bild 1: Vektordiagramm der Feldstärke in Achsrichtung einer Yagi-Antenne
(Is = Strom im Strahler, ID = Ströme in den Direktoren)
Sehr instruktiv ist auch das von E. und P. angegebene Vektordiagramm für die Feldstärke in einem entfernten Punkt auf der Antennenachse. Sie ist proportional dem resultierenden Vektor der Ströme in den Einzelelementen. Da die Ströme und Phasenwinkel in einer parasitär erregten Antenne nicht frei gewählt werden können, erlaubt diese in Bild 1 skizzierte Betrachtungsweise keine quantitativen Aussagen. Das Bild zeigt aber anschaulich, daß bei gegebenen Phasenwinkeln (Verzögerungszuwachs je Element) das Hinzufügen weiterer Elemente den resultierenden Vektor ab einem gewissen Punkt nicht mehr erhöht, sondern unter Umständen sogar verkleinert.
Der Verzögerungsbeitrag eines Elements und der darin erregte Strom ändern sich beide im gleichen Sinn wie seine Länge, so daß sich bei langen Antennen zwei Forderungen entgegenstehen: Um die Phasendrehung in Grenzen zu halten, müssen die Elemente kürzer gemacht werden, bis schließlich keine nennenswerten Ströme mehr darin fließen. Deshalb sind die sinnvolle Länge und der Gewinn einer Yagi-Antenne begrenzt.
E. und P., sowie die meisten anderen Experimentatoren untersuchten homogene YagiStrukturen, das heißt Anordnungen mit überall gleichen Abständen und Elementlängen. Für Antennen dieses Typs lassen sich zusammenfassend folgende Aussagen machen:
- Für jeden Wert der Antennenlänge gibt es einen zugehörigen Optimal-Wert der Phasengeschwindigkeit und somit der Gesamtverzögerung der Wellenfront. Die optimale Verzögerung wächst mit der Antennenlänge, jedoch nur bis zu einem Wert von ca. 105° oder 0,3 λ. Er wird zwischen 3 λ und 4 λ Länge erreicht und bleibt für längere Antennen konstant.
- Die Phasengeschwindigkeit V längs der Direktor-Kette hängt von Länge, Dicke und Abstand der Elemente ab. Es gibt unendlich viele Kombinationen, die zum Optimalwert von V führen. Bei Elementabständen von 0,4 λ und darunter wird immer der gleiche Maximalwert des Gewinns erreicht.
- Der maximale Gewinn hängt bei optimaler Wahl von V nur von der Antennenlänge ab.
- Der Gewinn zeigt ab etwa 6 λ keine nennenswerte Zunahme mehr; der Grenzwert beträgt ca. 14 dB. Bild 2 zeigt diesen Zusammenhang, sowie die Meßwerte von einigen käuflichen und selbstgebauten Antennen. Die Zahl am Ende der Kurzbezeichnung gibt die Elemente-zahl an.
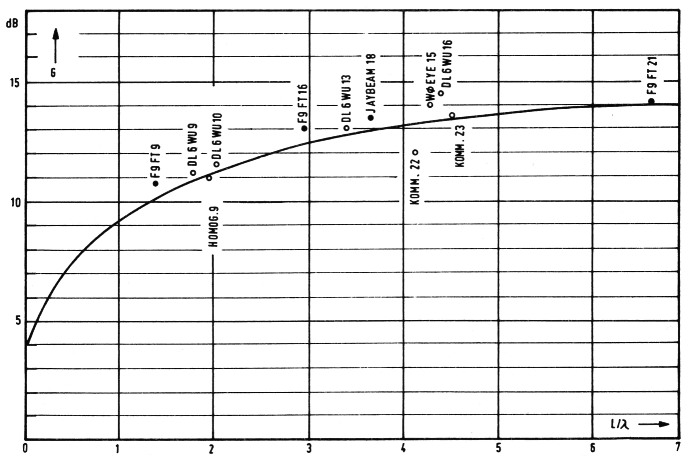
Bild 2: Durchgezogen: Gewinn von Yagi-Antennen In Abhängigkeit von der Länge (ab Strahler, nach Ehrenspeck und Poehler) Punkte: Meßwerte von DL1BU (•) und DL6WU (°)
2. Inhomogene Yagi-Antennen
Nachdem die obigen Aussagen für homogene Strukturen gelten, liegt es nahe, durch Abweichungen von der homogenen Form nach weiterer Verbesserung zu streben. Wegen der Vielzahl der Parameter ist jedoch ein zielstrebiges Experimentieren sehr erschwert. Es hat sich aber inzwischen erwiesen, daß es günstig ist, die Verzögerung mehr in Strahlernähe zu konzentrieren und zum fernen Ende hin auslaufen zu lassen(3),(4). Auch sollte die Strombelegung der Elemente vom Strahler weg fallende Tendenz haben(4). Beides zusammen läßt sich durch eine allmähliche Abnahme der Längen und Zunahme der Abstände erreichen.
Diese Maßnahmen bewirken gegenüber einer homogenen Struktur eine Reduzierung der Nebenzipfel bei gleichzeitiger Verbreiterung der Hauptkeule. Maximaler Gewinn tritt bei einem Kompromiß zwischen Richtschärfe und Nebenzipfelunterdrückung ein.
Auch müssen gegebenenfalls die Sprungstellen am offenen Ende und am Strahler, die zu Störungen der bei gut dimensionierten Antennen vorherrschenden Wanderwellen führen könnten, durch Korrekturen kompensiert werden.
Zwar sind die genannten Überlegungen zum Teil durch Computersimulation unterstützt worden, doch hat sich gezeigt, daß es ohne Probieren nicht geht. Deshalb sind die gesicherten Erkenntnisse über homogene Antennen, die in guter Näherung auch für die Mittelwerte inhomogener Antennen gelten, vor allem als Ausgangswerte von größtem Nutzen.
Es scheint ohnehin so, als ob alle Verbesserungen gegenüber dem Gewinn, wie er von E. und P. angegeben wurde, nur einen Zuwachs von rund 1 dB bringen. Der mit einfachen, ebenen Yagi-Strukturen maximal erzielbare Gewinn dürfte deshalb nicht wesentlich über 15 dB liegen.
Gegenüber den in manchen Veröffentlichungen genannten höheren Maximalgewinnen (z.B. 5,6) ist erhebliche Skepsis am Platz. Meist handelt es sich um aus Richtdiagrammen zurückgerechnete oder durch Bodenreflexionen verfälschte Werte. Fehler von 3 dB sind keine Seltenheit. Über Gewinnmessungen wird noch zu sprechen sein.
In einer erst nach Fertigstellung des Manuskripts zur Kenntnis des Verfassers gelangten Arbeit(9) wird die Möglichkeit angedeutet, durch gezieltes Ausnutzen der Endreflexion eine weitere (kleine) Gewinnsteigerung zu erreichen, doch scheint die Dimensionierung sehr kritisch zu sein.
3. Eigenbau von Yagi-Antennen
Der Selbstbau von Antennen ist nach wie vor lohnend, besonders wenn große Anlagen erstellt werden sollen. Für den Entwurf bietet sich ein Modellaufbau im 70-cm-Band an, mit anschließendem Umrechnen auf die Arbeitsfrequenz. Aber auch, wer erprobte Auslegungen nachbauen, abwandeln, oder auf andere Bänder übertragen möchte, sollte den Einfluß aller Konstruktionsparameter auf die Funktion der Antennen kennen. Scheinbar geringfügige Abweichungen können totalen Mißerfolg nach sich ziehen!
Die maßgebenden Größen sind: Antennenlänge, Elementabstände, Elementlängen, Elementdicke und gegebenenfalls die Dicke des Trägerrohres.
3.1. Elementlänge und -dicke
Bild 3 zeigt die Abhängigkeit der Elementlängen für Reflektor, Strahler und Direktoren (als Mittelwert für alle Direktoren) einer in ihren sonstigen Abmessungen festgelegten Antenne von der Elementdicke. Es mag erstaunen, daß als Parameter nicht Antennenlänge und Elementabstand sondern nur die Elementezahl erscheint.
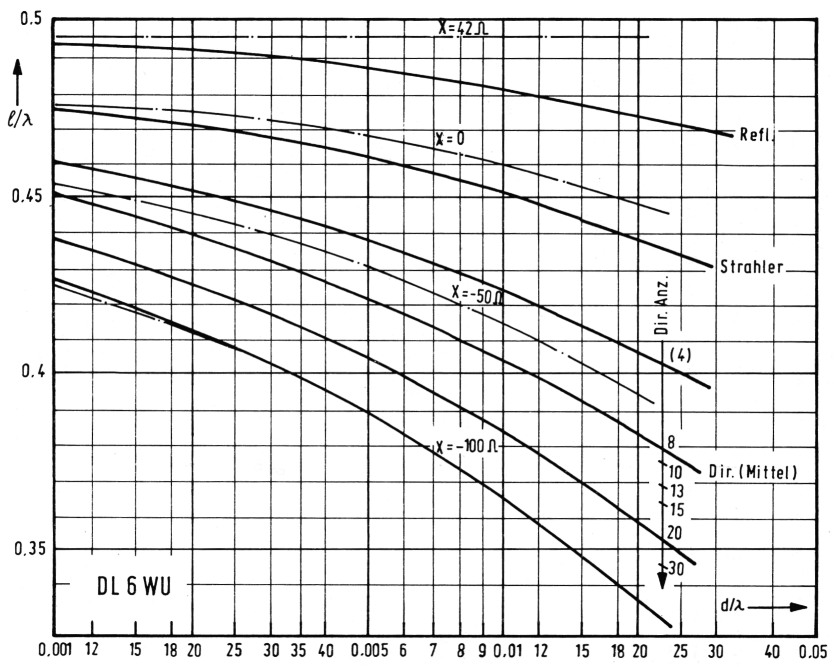
Bild 3: Optimale Länge von Yagi-Elementen in Abhängigkeit von der Dicke.
Gestrichelt: Kurven konstanten Blindwiderstands
Das hat seinen Grund im reziproken Zusammenhang zwischen Phasenverzögerung und Elementabstand(7). Da bei langen Antennen, wie in Abschnitt 1 erwähnt, die optimale Verzögerung praktisch konstant bleibt, fallen die Kurven für gleiche Elementezahlen zusammen. Für kurze Antennen gilt das nicht mehr, jedoch ist die Näherung in jedem Fall brauchbar.
Man erkennt, daß die Dickenabhängigkeit der Länge bei den Direktoren größer ist, als bei Strahler und Reflektor, und mit wachsender Elementezahl zunimmt. Das kommt daher, daß Strahler und Reflektor fast in Resonanz betrieben werden, die Direktoren aber stark kapazitiv verstimmt. Mit wachsender Elementdicke sinkt die Güte der durch die Elemente dargestellten Resonanzkreise und die Verstimmung muß, um die gleiche Phasenlage zu erzielen, weiter vergrößert werden. In der hier gewählten halblogarithmischen Darstellung ist gut zu erkennen,. daß für die bei VHF und UHF gebräuchlichen Elementdicken eine Verzehnfachung des Durchmessers bei Strahler und Reflektor eine Verkürzung von ca. 7%, bei den Direktoren sogar rund 14% nach sich zieht!
Gestrichelt eingezeichnet sind die Ortskurven konstanter Reaktanz für ein einzelnes Dipol-element. Aus der großen Ähnlichkeit des Verlaufs kann man schließen, daß für die Funktion eines Elements vor allem seine Reaktanz maßgeblich ist, die beim Ersatz durch ein Element anderer Dicke wieder hergestellt werden muß. Der Realteil der Impedanz, also Verlust- und Strahlungswiderstand, hängt in der Nähe von λ/2 nur sehr wenig von Länge und Dicke ab.
Auch zur Umrechnung von Elementen verschiedener Dicke läßt sich das I/d-Diagramm daher sehr vorteilhaft verwenden: man sucht für das bekannte Element das zugehörige Wertepaar (I1, d1) auf, interpoliert eine Kurve parallel zu den nächstliegenden Kurven des Diagramms und liest für den Schnittpunkt mit der neuen Dicke d2 die neue Länge I2 ab.
Sind die Elementlängen nennenswert gestaffelt, muß das Verfahren für jedes Element wiederholt werden. Meistens genügt aber die Berechnung der Differenz zwischen alter und neuer durchschnittlicher Länge und entsprechende Korrektur der einzelnen Elementlängen. Die Längentoleranz des einzelnen Elements ist übrigens relativ groß.
Bei Antennen bis zu 4 λ Länge war kein signifikanter Einfluß der Elementdicke auf den Gewinn feststellbar. Die untersuchten Durchmesser reichten von 0,003 λ bis 0,015 λ. Bei sehr dünnen Elementen aus Messing wurde allerdings eine Gewinnminderung beobachtet, die auf Skin-Effekt-Verluste schließen läßt.
3.2. Einfluß der Tragrohr-Dicke
Über den Einfluß der Elementhalterung gibt es kaum Angaben. Gelegentlich findet man als Daumenwert, daß bei Elementen, die einen metallischen Träger durchdringen, 2/3 der Trägerdicke zu addieren seien.
Es wurde zunächst versucht, durch Vergleiche zwischen errechneter und gemessener Resonanzlage verschiedener Antennen hierauf Rückschlüsse zu ziehen, was jedoch sehr ungenau ist und nur eine grobe Tendenz liefert.
Deshalb wurden eigene Messungen durchgeführt. Die Verstimmung einer angepaßten DreiElement-Antenne durch Veränderung des (langen) Elementträgers im Bereich des Direktors wurde durch Neuabstimmen des Direktors kompensiert. Es ergab sich die in Bild 4 gezeigte Kurve, die für die Praxis schon ausreichend genau sein dürfte. Ein Einfluß der Trägerform (Kreis-, Rechteck- oder U-Querschnitt) konnte nicht gefunden werden.
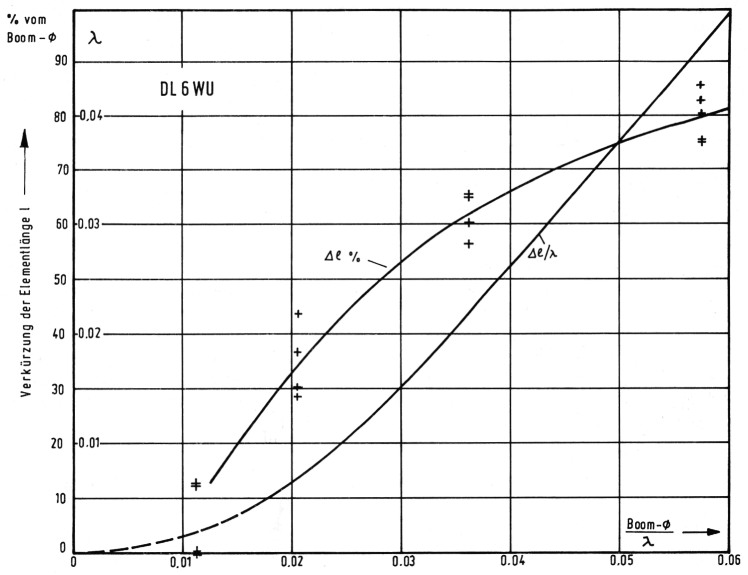
Bild 4: Längenkorrektur für Elemente, die einen metallischen Träger durchdringen
3.3. Anpassung
Ein kritischer Punkt bei der Konstruktion von Parasitär-Antennen ist die Anpassung an die Speiseleitung.
Den Strahlungswiderstand des gespeisten Elements beeinflussen viele Parameter: seine eigene Länge, Länge und Abstand der Nachbarelemente, aber auch deren Lage zueinanc er. Erst die weiter entfernten Direktoren (etwa ab Nr.4) haben nur noch geringen Einfluß. Der Zusammenhang ist außerordentlich komplex. Im allgemeinen drückt ein Näherrücken der Nachbarelemente an den Strahler dessen Speisewiderstand, ebenso ein Annähern der Eigenresonanz dieser Elemente an die Arbeitsfrequenz. Bei sehr kleinen Abständen kann sich diese Tendenz jedoch umkehren, wobei offensichtlich die (durchmesserabhängige) kapazitive Kopplung maßgebend ist. Ein langer erster Direktor in großer Nähe des Strahlers wirkt wie ein Element eines Faltdipols. Durch entsprechende Wahl der Parameter ist es beispielsweise möglich, mit einem Schleifendipol Anpassung an 240 Ω oder direkt an 75 Ω zu erzielen. Man ist hier auf systematisches Probieren angewiesen.
Sehr bewährt haben sich zwei Verfahren: man betreibt die zu optimierende Antenne entweder als Sendeantenne an einem sehr langen Speisekabel (Verluste 3 dB oder mehr) oder als Empfangsantenne an einem guten Abschlußwiderstand. In beiden Fällen wird einfach auf maximale Empfangsspannung getrimmt. Anschließend kann man nach dem Reflektometer den Feinabgleich vornehmen - wenn überhaupt noch nötig. Man vermeidet so auf jeden Fall den Fehler, die Antenne zwar sauber angepaßt, aber völlig verstimmt zu haben.
3.4. Gewinnmessungen
Exakte Messungen an Antennen sind problematisch, besonders Gewinnmessungen. In DIN 45003 sind die Anforderungen zusammengestellt. Vor allem die dort aufgezeigten Maßnahmen zum Ausschluß von störenden Bodenreflexionen werden bei Amateurmessungen meist grob vernachlässigt. Mit unseren Mitteln kann normalerweise außer der Anpassung nur das Horizontaldiagramm gemessen werden, das heißt bei horizontaler Polarisation das E-Diagramm. Da bei Yagi-Antennen ein relativ enger Zusammenhang zwischen E- und H-Diagramm besteht (Bild 5), bekommt man so wenigstens einen Anhalt. Setzt man die gefundenen Werte jedoch in das Gewinn-Nomogramm(6) ein, so erhält man zwar eine theoretische Obergrenze für den Gewinn, für die Praxis jedoch mit Sicherheit zu gute Werte, denn im Diagramm sind verlustlose Antennen ohne Nebenzipfel vorausgesetzt. Besonders bei sehr langen Antennen wachsen die Nebenzipfel und damit auch die Verluste mit der Länge rasch an.
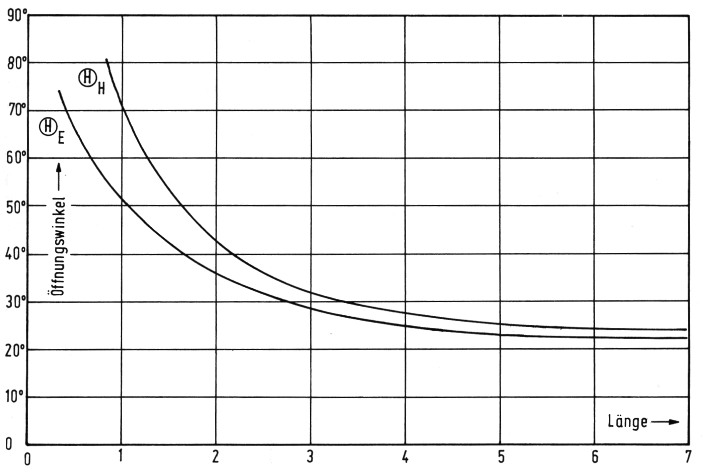
Bild 5: Öffnungswinkel von Yagi-Antennen in Abhängigkeit von der Antennenlänge (Mittelwerte aus zahlreichen Angaben und Meßwerten)
3.4.1 Einfluß von Nebenzipfeln auf den Gewinn
Ausgangspunkt aller Gewinnabschätzungen aus der Diagrammform ist der Öffnungswinkel 0 der Hauptkeule (Winkel zwischen den 3-dB-Punkten). Man denkt sich die Antenne im Mittelpunkt einer Kugel und setzt das von der Hauptkeule ausgeleuchtete Stück Oberfläche bzw. Raumwinkel ins Verhältnis zur Oberfläche der Vollkugel, die ein isotroper Strahler gleichmäßig beleuchten würde. Unter Voraussetzung gleicher Eingangsleistung und Vernachlässigung von Nebenzipfeln ist der Gewinn gleich dem Kehrwert des Verhältnisses der Oberflächen.
Da die Energieflußdichte innerhalb der Hauptkeule ortsabhängig ist, sind je nach angenommener Form der Keule Korrekturen für die wirksame Fläche erforderlich. Die jüngste Abschätzung für den Gewinn lautet nach (8):
Gi = 32 in 2 / (Ø2E + Ø2H) (Winkel im Bogenmaß).
Um eine Vorstellung von der Größe des durch Nebenzipfel verursachten Verlusts zu erhalten, wurde versucht, eine ähnliche Überlegung für ein typ. Yagi-Diagramm anzustellen (Bild 6).
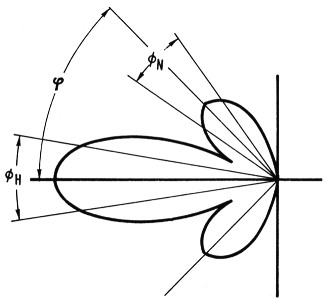
Bild 6: Schematisiertes, typisches Diagramm einer Vagi-Antenne mit einer Nebenkeule
Angenommen sei eine Hauptkeule mit ØH = 24°, das heißt mit 3-dB-Punkten bei ± 12° und eine Nebenkeule mit dem Maximum bei φ = ± 36° und ØN = 12°. Das Diagramm sei rotationssymmetrisch zur Achse φ = 0°, was für lange Yagi-Antennen annähernd zutrifft. Die von den Keulen eingenommenen Raumwinkel O (Oberflächenteile der Einheitskugel) berechnen sich dann wie folgt: O = 2 π (1 - cos φ)
Für die Hauptkeule mit φ = 12° : OH = 0,138
Für die Nebenkeule: ON = O42° - O30° = 0,835
Das heißt, die Nebenkeule bedeckt die 6fache Fläche der Hauptkeule! Da man sich die Nebenkeule trichterförmig um die nadelartige Hauptkeule herum denken muß, ist das nicht weiter verwunderlich. (Um die Rechnung einfach zu halten, wurde die 3-dB-Fläche als Wirkfläche angenommen. Weil jedoch nur das Verhältnis der Flächen interessiert, darf man annehmen, daß der Fehler nicht ins Gewicht fällt.
Der gesamte Energiefluß P der Antenne verteilt sich auf Hauptkeule (PH) und Nebenkeule (PN) im Verhältnis von deren Raumwinkeln, multipliziert mit dem Wert der Nebenzipfeldämpfung NN, also PH/PN = NN × OH/ON.
Da P = PH + PN = const., steht der Hauptkeule nur noch ein entsprechend geringerer Anteil der gesamten Energie zur Verfügung und der Gewinn wird im gleichen Verhältnis reduziert.
Die Gewinnminderung beträgt
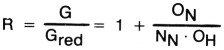
Für unser Beispiel mit ON/OH = 6 heißt das:
| NN | R |
|---|---|
| 6 (7,8 dB) | 2,00 (3,00 dB) |
| 10 (10,0 dB) | 1,60 (2,00 dB) |
| 20 (13,0 dB) | 1,30 (1,14 dB) |
| 50 (17,0 dB) | 1,12 (0,50 dB) |
Man sieht, daß in diesem Fall bei 7,8 dB Nebenzipfeldämpfung die halbe Energie nutzlos "entweicht", der Gewinn also halbiert wird.
Nimmt man für die Musterantenne mit ØE = OH = 24° die Nebenzipfeldämpfung NN zu 13 dB an, so ergibt sich folgende Gewinnrechnung:
Gi = 55,7 = 17,5 dB (über isotropen Strahler)
GD = Gi - 2,14 dB = 15,36 dB (über Dipol)
GD red = GD/R = 14,22 dB (über Dipol)
Dieser Wert stimmt gut überein mit den bei langen Yagi-Antennen gemessenen Gewinnwerten. Der Klarheit halber muß gesagt werden, daß dies zwar ein recht typisches Beispiel ist, daß aber natürlich Lage und Breite der Nebenzipfel von Antenne zu Antenne variieren. Die Tendenz ist jedoch eindeutig: der Einfluß der Nebenzipfel wächst mit zunehmender Richtschärfe. Auch können die Rückwärtskeule und die Nebenzipfel höherer Ordnung nicht immer vernachlässigt werden.
3.5. Abschließende Hinweise
Bei Diagramm-Messungen und Antennenvergleichen sollte man übrigens immer auf einen exakten Abschluß achten. Die meisten Empfängereingänge verursachen eine erhebliche Fehlanpassung der Leitung, was bei geringen Kabellängen zu einer verstimmenden Rückwirkung auf die Antenne führen kann. Ein 10-dB-Dämpfungsglied wirkt hier manchmal Wunder.
Noch einige Worte zu der vom Verfasser benutzten Versuchsanordnung. Für die Vorversuche im Garten wurde eine Alu-U-Schiene benutzt, in die auf Messingklötzchen aufgelötete Elemente verschiebbar eingesetzt werden konnten. Im 70-cm-Band sind die Dimensionen sehr handlich. Die gefundenen Längen- und Abstandswerte wurden in Karteiform festgehalten.
Für genaue Messungen stand in größeren Zeitabständen die große reflexionsfreie Trichterkammer des FTZ zur Verfügung, wo dann besonders interessant erscheinende Anordnungen mit professionellen Meßmitteln untersucht werden konnten. Ein typisches Beispiel sei hier erwähnt: ein rund 2 λ langer homogener Yagi nach Ehrenspeck-Daten zeigte 11,0 dB Gewinn und wich damit nur 0,15 dB vom "Sollwert" nach Bild 2 ab. Eine daraus abgeleitete 10-Element-Antenne gleicher Länge hatte bei von 34° auf 36° erhöhtem Öffnungswinkel 11,5 dB Gewinn und um fast 10 dB abgesenkte Nebenzipfel. Zum Vergleich zeigte eine käufliche Antenne doppelter Länge nur 0,5 dB mehr Gewinn.
Besonders danken möchte der Verfasser den Herren Hollman, Dr. Lorenz und Seher vom Forschungsinstitut der DBP für die Unterstützung, sowie den Funkamateuren Vollhardt, DL3NQ, Dr. Dambold, DJ5DT, Weßner, DB5FU, und Napierski, DJ6NS, für ihre Hilfe bei den Messungen. Günter Schwarzbeck, DL1BU, stellte wertvolle Daten und Meßergebnisse zur Verfügung.
4. Literatur
- Yagi, H.: Beam transmission of ultra short waves, Proc. IRE, Juni 1928, Seite 715 - 741
- Ehrenspeck, H.W., Poehler, H.: A new method for obtaining maximum gain from Yagi antennas, IRE Trans. Ant. Prop, Oktober 1959, Seite 379 - 386
- Heilmann, A.: Antennen I - III, BI-Hochschultaschenbücher
- Chen, CA., Cheng, D.K.: Optimum element lengths for Yagi-Uda arrays, IEEE Trans. Ant. Prop, Januar 1975, Seite 8 - 14
- Greenblum, C.: Notes on the development of Yagi arrays, QST, August 1956, Seite 11 - 17, 114, 116
- Brier, H.S., Orr, W.I.: VHF handbook for radio amateurs, Radio Publications, Wilton, Conn.
- Spector, J.O.: An investigation of periodic rod structures for Yagi aerials, Proc. IEE Part B, Januar 1958, Seite 38 - 44
- Tai, Chen-To; Pereira, C.S.: An approximate formula for calculating the directivity of an antenna, IEEE Trans. Ant. Prop., März 1976, Seite 235 - 236
- Bojsen, J.H. et al: Maximum gain of Yagi-Uda arrays, Electronics Letters, September 1971, Seite 531 - 532
DL6WU, Günter Hoch.