Ruis 2
2. Thermische ruis
De belangrijkste ruis is de thermische ruis (ook wel Johnson of witte ruis genoemd), welke wordt opgewekt in elke geleider, als gevolg van in beweging gebrachte vrije elektronen, door warmte.
De open ruisspanning wordt gegeven door:
![]()
Waarbij:
K = Boltzmankonstante 1,38×10-23 J / K
T = Absolute temperatuur, K
R(f) = Weerstand als funktie van de frequentie
p(f) = Plancks faktor
df = Verschilfrequentie, Hz
Planck faktor:
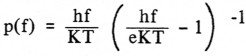
waarbij h de Planck-konstante is, 6,62×10-34 Js.
Indien ![]() klein is, wordt Plancks faktor ongeveer 1 (tot frequenties van 6˜1012 Hz is dit bruikbaar).
klein is, wordt Plancks faktor ongeveer 1 (tot frequenties van 6˜1012 Hz is dit bruikbaar).
Als de impedantie binnen de frequentieband konstant blijft, wordt de eerste formule:
![]()
Waarbij:
B = Bandbreedte (Hz)
Het maximale ruisvermogen, welke van een ruisbron betrokken kan worden, bedraagt, indien de externe impedantie gelijk is aan de ruisbronimpedantie:
![]()
Indien de twee impedanties beide dezelfde temperatuur bezitten, zal er geen ruisvermogensoverdracht plaatsvinden, ongeacht hun weerstandswaarden.
3. Defenities
Excess noise ratio (met betrekking tot een ruisbron) E.N.R.
Dit is de verhouding in vermogen, van een uitgeschakelde ruisbron (T = 290 K) en een ingeschakelde ruisbron, uitgedrukt in dB.
Voor een met argon gevulde ruisbuis is dit b.v. 15,5 dB.
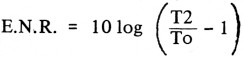
Ruisgetal
Het ruisgetal is de verhouding tussen de signaal/ruis verhouding aan de ingang en de signaal/ruis verhouding aan de uitgang van een vierpool (versterker, ontvanger, etc.).
Dit is een verhouding, dus een onbenoemd getal, welke echter ook in dB wordt uitgedrukt.
Operating noise temperature
Deze wordt gegeven door de formule:
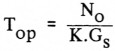
Waarbij:
No = het ruisvermogen per bandbreedte-eenheid, welke in het uitgangscircuit gemeten wordt.
4. Ruisbronnen
a. Thermische ruisbron
Dit is een geleider met een bekende weerstand, welke in een vloeibaar koelmiddel (helium) is ondergedompeld.
Door de lage "koud" temperatuur (78 K) is er een zeer laag ruisvermogen beschikbaar. Deze ruisbron wordt dan ook gebruikt voor ontvangers met een zeer laag ruisgetal en door zijn grote nauwkeurigheid ook als referentie voor andere soorten ruisbronnen. De nauwkeurigheid wordt bepaald door de oven nauwkeurigheid, de zuiverheid van het koelmiddel en de atmosferische druk.
Nauwkeurigheid is ±2 K (frequentiebereik van 0 tot 6 GHz).
b. Gas ontladingsruisgeneratoren
Deze bestaat uit een buis welke is gevuld met een gas (neon of argon).
De buizen zijn voor alle frequentiebanden verkrijgbaar.
Voor hoge frequenties worden de buizen onder een hoek van 10° tot 15° in een golfpijp gemonteerd, om een minimale staande golf verhouding te verkrijgen.
De excess noise ratio is afhankelijk van het soort gas, gasdruk, diameter van de buis en de stroom door de buis.
Voor een met argon gevulde buis is dit ca. 15,5 dB en voor neon 17,2 dB bij een buis stroom van ca. 175 mA (ruistemperatuur 10.000 - 20.000 K).
Indien de verzadigingsstroom is bereikt, dan blijkt het ruisvermogen slechts weinig op een stroomverandering te reageren.
Bij 1% stroomverandering slechts 0,1% of 0,004 dB ruisvermogen verandering.
De veroudering bedraagt hooguit 0,03 dB na 10.000 uur bedrijf, bekeken bij 100 buizen.
Totale nauwkeurigheid van ±0,25 dB is normaal bereikbaar.
c. Diode ruisbron
Deze ruisbron bestaat in principe uit een diode, waar de verzadigingsstroom doorloopt (voorbij de knie in de I/U karakteristiek) al of niet geihtegreerd met een versterker. Voorbij dit punt is het afgegeven ruisvermogen nagenoeg recht evenredig met de stroom door de diode en de uitgangsimpedantie.
De diode ruisbronnen zijn bruikbaar vanaf 1 MHz tot ca. 35 GHz, doch zijn door de hogere staande golf verhouding iets onnauwkeuriger dan de gas ruisbronnen (± 0,5 dB). Er zijn hoge ruisvermogens mogelijk -72 dBm/MHz, waardoor de toepassing ook op minder gevoelige ontvangers mogelijk is.
De excess noise ratio bedraagt:
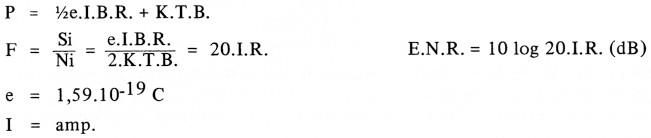
5. Referentie ruisvermogen
Hiermede wordt bedoeld het ruisvermogen, wat bij een absolute temperatuur van 290 K (17 °C) wordt opgewekt in een geleider (weerstand), bij een frequentie bandbreedte van 1 MHz.
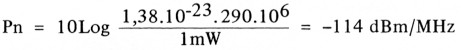
Wil men het ruisvermogen weten bij een andere bandbreedte, dan moet men de 10 Log uit de frequentieverhouding er bij optellen.
Voorbeeld:
Pn = -114 dBm/MHz
Gevr. het ruisvermogen in 1 kHz bandbreedte.

6. Ruistemperatuur (Te)
Een andere manier om de ruisproduktie van een versterker op te geven is het opgeven van de ruistemperatuur.
Dit wordt gedaan in K.
0 K komt overeen met een ruisgetal van 0 dB.
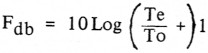
Waarbij:
To = de referentie temperatuur van 290 K
Te = de effectieve ruistemperatuur
Fdb = ruisgetal in dB
7. Ruisgetal (Ruisfaktor)
Er zijn verschillende methoden om de ruisbijdrage van een versterker of ontvanger in cijfers uit te drukken.
Deze ruisbijdrage wordt ook wel de "ruisfaktor" genoemd en wordt als "ruisgetal" in cijfers uitgedrukt, onbenoemd of in dB.
Voor kwaliteitsontvangers wordt het ruisgetal of ruistemperatuur opgegeven, terwijl bij de meer commerciele ontvangers vaak het aantal µV ingangsspanning voor 10 dB signaal/ruis verhouding (AM) aan de uitgang wordt opgegeven (of 26 dB signaal/ruis verhouding bij FM ontvangers).
Hier spreekt men over de gevoeligheid van de ontvanger.
Het is begrijpelijk dat de gevoeligheid van de ontvanger wordt bepaald door de ruisfaktor, er is dan ook een bepaald verband tussen ruisgetal en gevoeligheid.
Het omrekenen van ruisgetal naar gevoeligheid gaat als volgt:
![]()
Waarbij:
![]() = Signaal/ruis verhouding aan de uitgang van de ontvanger
= Signaal/ruis verhouding aan de uitgang van de ontvanger
Fr = Ruisgetai van de ontvanger
Smin = Het minimaal te ontvangen signaal
K = Boltzman konstante
T = Absolute temperatuur
B = Frequentie bandbreedte
Het opgeven van de gevoeligheid van de ontvanger is niet gestandariseerd en is daarom ook geen objectieve beschouwing van de kwaliteit van een ontvanger.
Het ruisgetal geeft volgens de definitie aan, hoeveel maal de signaal/ruis verhouding in een netwerk slechter is geworden.
In formule:
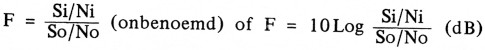
Waarbij:
i = ingang
o = uitgang
In een ideale versterker zal er geen ruin aan het signaal toegevoegd worden, de verhoudingen blijven gelijk en het ruisgetal zal 1 bedragen.
![]()
Waarbij:
So het maximaal beschikbare uitgangssignaal is.
De verhouding So/Si is de vermogensversterking G.
Ni is het ruisvermogen K.T.B.
Voor twee in cascade geschakelde netwerken wordt dit:
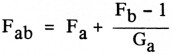
Fab = het totale ruisgetal
Fa = ruisgetal van netwerk a
Fb = ruisgetal van netwerk b
Deze formule kan op analoge wijze voor meerdere netwerken worden uitgebreid.
8. Hoe meten we het ruisgetal
Ook hier zijn verschillende methoden voor, afhankelijk van de snort ruisbron of meetzender.
a. De 3 dB methode
(alleen voor een ruisbron met variabel ruisvermogen)

ruisgenerator / ontvanger of 3 dB verzwakker / detector / D.C. meter / versterker
Sluit het geheel aan volgens bovenstaand schema.
Ruisgenerator uit en verzwakker op 0 dB.
Lees de gelijkspanning of van de meter en onthou deze waarde.
Zet de verzwakker op 3 dB en schakel de ruisgenerator aan.
Voer nu de stroom door de ruisgenerator op totdat de meter weer de eerstgevonden gelijkspanning aangeeft.
Het ruisgetal is nu:

Bij deze meting is het niet nodig om de bandbreedte te weten om het ruisgetal te bepalen.
De 3 dB verzwakker dient ervoor om, onafhankelijk van de detector karakteristiek, zuiver te kunnen meten.
b. Y factor methode (Hold/cold methode)
Sluit het geheel aan als bij punt a, nu echter met een variabele verzwakker.
Meet een uitgangsspanning bij uitgeschakelde ruisbron.
Schakel de ruisbron in.
Draai de verzwakker terug tot de eerst gevonden uitgangsspanning weer is bereikt.
De verandering in verzwakking is de Y factor.
Het ruisgetal wordt nu:
![]()
Waarbij:
Tex = Excess noise power van de ruisbron
c. Meetzender methode
Voor deze methode is noodzakelijk dat de ruisbandbreedte bekend is (eventueel meten met de meetzender). Zie noot.
De meetzender dient dezelfde uitgangsimpedantie te hebben als de ingangsimpedantie van de ontvanger.
Sluit de meetzender aan op de ontvanger, doch uitgeschakeld.
Meet de gelijkspanning op de detector uitgang van de ontvanger.
Schakel de meetzender in en draai het uitgangsvermogen op totdat de gelijkspanning op de detector 1,45 maal de eerst gevonden waarde is (aangenomen dat de detector lineair is en de AGC niet in werking treedt).
Het ruisgetal is nu:
![]()
Waarbij:
Si = signaalvermogen van de generator
K = 1,38×10-23 J/s.
T = 290 K
B = bandbreedte (Hz)
Noot:
De 3 dB bandbreedte kan bij benadering als ruisbandbreedte worden beschouwd.
Deze behoeven echter niet gelijk te zijn.
De ruisbandbreedte is praktisch altijd groter.
9. Fouten die we maken tijdens de meting
De belangrijkste fouten die we kunnen maken zijn:
- Als de temperatuur belangrijk afwijkt van de 290 K (17°C). De fout welke gemaakt wordt is des te groter naarmate het ruisgetal kleiner wordt.
- b. Door een slechte staande golf verhouding. Als de aanpassing van ruisbron en ontvanger niet optimaal is, zal er onvoldoende energie-overdracht zijn.
- c. Indien van een superheterodyne ontvanger zonder hoogfrequent preselectie het ruisgetal bepaald moet worden, zal het ruisgetal 3 dB te hoog zijn, omdat de ontvanger de ruis meet welke zowel op de ontvangstfrequentie als op de spiegelfrequentie binnenkomt, dus 2 maal.
Deel 1 - Deel 2.
PA0SJG.