Rekenen met ruisgetal en ruistemperatuur 1
Het ruisgetal van een ontvanger of versterker wordt tegenwoordig steeds vaker vermeld. Een ruisgetal dat erg laag is verzekert volgens velen succes. Daarbij wordt echter voorbijgegaan aan andere ruisbronnen zoals de coaxkabel tussen de antenne en de versterker. In het navolgende artikel zal worden uiteengezet hoe men met ruisgetallen, ruisvermogens en ruistemperaturen een systeem dat met ruis behept is kan beschrijven.
1. Het vermogen van een ruisbron
Ruis is een signaal dat in het algemeen bekend staat als een sissend geluid. Bekijkt men ruis op een oscilloscoop, dan blijkt dat ruis een chaotisch en volkomen onvoorspelbaar signaal voorstelt. Toch kan men wel iets zeggen van hetgeen men op het scherm ziet: het blijkt dat hoge pieken zeldzamer zijn dan kleine uitwijkingen, het gemiddelde van al de uitwijkingen is nul, en het vermogen van de ruis is ongelijk nul. Men kan een effektieve waarde aan de ruis toekennen.
Het is handig om met vermogens to werken, daar vooral op het hoogfrequente gebied de vermogensversterking of verzwakking bekend is. Bovendien mag men de vermogens van twee bronnen die in serie staan bij elkaar optellen, mits de twee bronnen onafhankelijk van elkaar ruisen. In de meeste systemen geldt deze regel wel, en iets verderop zal er van die somregel gebruik gemaakt worden.
2. De ruis van een weerstand
Het is een "natuurwet" dat elk systeem dat energie op kan nemen en kan overdragen behept is met ruis. Een versterker, een weerstand, of b.v. een batterij genereren spontaan ruis.
In een weerstand bewegen elektronen zich, door temperatuursagitatie, veel sneller dan de stroom die er door loopt. Deze extra beweging bezit geen vaste richting en is onafhankelijk van de stroom die door de weerstand loopt. Het resultaat is een ruisspanning over de weerstand. Het gemiddelde ruisvermogen is afhankelijk van de temperatuur en van de bandbreedte waarmee men meet. Het vermogen dat wordt gegenereerd is echter niet afhankelijk van de weerstand of van de frequentie, en het frequentiespektrum is dan ook "wit". De effektieve spanning over de weerstand is wel afhankelijk van de weerstandswaarde. De formule voor de effektieve ruisspanning luidt:
ueff = √4kTRB
Hierin is:
T de absolute temperatuur in Kelvin,
k is de Boltzmannconstante (k = 1,38.10-23 J/K),
R is de weerstand in Ohm en
B de bandbreedte in Hertz.
We kunnen nu ook omgekeerd redeneren: als men een bepaalde ruisspanning weet dan kunnen we de temperatuur b.v. vast kiezen en de weerstand zo groot maken dat de formule weer past. Deze weerstand kan men dan als een "equivalente ruisweerstand" definieren. Evenzo kan men de weerstand vast kiezen en de temperatuur ervan aanpassen: de "equivalente ruistemperatuur". Vooral de laatste, de ruistemperatuur, wordt veel toegepast.
3. De ruistemperatuur van een tweepoort
Een tweepoort is een systeem waarin het inkomende signaal een eenduidig verband heeft met het signaal dat er weer uitkomt, b.v. versterkers, mixers, coaxkabels, enz. Sluit men een ruisende weerstand aan op een tweepoort, dan kan de weerstand een ruisvermogen overdragen aan de tweepoort.
Bekijken we nu figuur 1A. In deze schakeling heeft de ruisbron bovendien nog een extra bron in de tweepoort zelf. In figuur 1B zijn de twee bronnen aan de ingang getekend, terwijl de weerstand en de tweepoort beide ruisvrij verondersteld zijn.
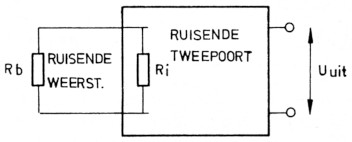
Fig. 1A. Een ruisend systeem
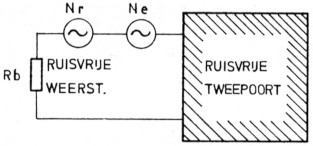
Fig. 1B. Ruisvrij systeem met equivalente ruisbronnen
Is nu de ingangsweerstand Ri gelijk aan de bronweerstand Rb, dan is de vermogensoverdracht maximaal. Is de schakeling in thermisch evenwicht dan is het uitwisselbare vermogen:

Dit uitwisselbare vermogen is het vermogen dat de ruisende weerstand maximaal aan de tweepoort kan overdragen.
De tweepoort echter ruist zelf ook en men kan deze eigenruis voorstellen als een extra bron aan de ingang. Het vermogen van deze ruisbron kan men optellen bij het vermogen dat de weerstand afgeeft, zodat het totale vermogen gelijk is aan:
N = Nr + Ne, met Ne als het vermogen van de eigenruis van de versterker.
Dus als de weerstand Rb niet zou ruisen, dan zou er toch nog ruis geproduceerd worden. Men kan aan de weerstand Rb dus een extra temperatuur toekennen, en deze extra temperatuur is de "equivalente ruistemperatuur" van de versterker.
Anders gesteld: om het vermogen Nr plus Ne op te wekken moet de temperatuur van Rb verhoogd worden van T tot T + Te.
Bij metingen neemt men voor T de standaardtemperatuur van 290 Kelvin (170° C), maar het kan ook voorkomen dat T veel groter is (ruisbron) of dat T veel kleiner is (antenne die op de "koude" hemel gericht staat).
4. Het ruisgetal
In het bovenstaande is de eigenruis van een versterker voorgesteld als een verhoging van de temperatuur van de bronweerstand. De mate waarin dit gebeurt kan men vastleggen in een mast voor eigenruis. Dit heet de ruisfaktor F en die stelt de verhouding voor tussen bronruis + eigenruis en de bronruis:

Hierin is T de standaardtemperatuur van 290 K en Te de equivalente ruistemperatuur van de versterker.
Opzettelijk wordt hier van de ruisfaktor F gesproken om verwarring te voorkomen met het ruisgetal NF wat in decibels wordt uitgedrukt:
NF = 10 logF (4)
Om nu deze gortdroge theorie wat te verlichten volgt er een voorbeeld.
Gesteld dat de ruistemperatuur van een voorversterker 75 Kelvin is. Wat is het ruisgetal?
Oplossing: NF = 10 log (1 + Te/T) = 10 log (1 + 75/290) = 1 dB.
5. Het meten van het ruisgetal met een ruisgetalmeter
Om het ruisgetal te meten, kan men aan de ingang van de ontvanger een bron plaatsen die periodiek aan- en uitgeschakeld wordt. Men moet dan het extra vermogen kennen dat de bron Levert als die aan staat. Aan de uitgang van de ontvanger meet men de verhouding tussen het vermogen als de bron uit staat resp. aan staat. Deze verhouding is aan de uitgang van de ontvanger kleiner dan aan de ingang, omdat de ontvanger zelf ook ruist. We kunnen als het ware de mate waarin de bronruis verdrinkt in de ontvangerruis meten.
Als men met een automatische ruisgetalmeter werkt, dan is de bron meestal goed bekend. Op de bron staat dan de Excess Noise Ratio gegeven:

Hierin is TO de ruistemperatuur van de bron in de uit-stand en Taan de ruistemperatuur van de aan-stand. Men kiest voor TO meestal de standaardtemperatuur van 290 K omdat de bron in de uit-stand alleen thermische ruis van de inwendige weerstand levert. Is de werkelijke temperatuur van de inwendige weerstand niet 290 K dan kan dat een fout opleveren in de meting van het ruisgetal. Vooral als het ruisgetal al erg laag is (kleiner dan 1 dB) dan wordt de onzekerheid mede door deze afwijking in de ENR van de gegeven waarde belangrijk. Andere oorzaken van afwijkingen zijn SWR-verlies en to slechte spiegelfrequentie onderdrukking. Al deze fouten maken dat een ruisgetalmeting bij de ene meetdag b.v. 0,6 dB NF oplevert, terwijl bij een andere meting de NF 0,9 dB is. Fouten kunnen elkaar wel opheffen, maar meestal geldt de Wet van Behoud van Ellende die zegt dat alle fouten bij elkaar opgeteld worden. Maar nu weer even terug naar de theorie.
Aan de uitgang van de ontvanger meet men een ruisvermogen dat gemiddeld N1 is als de bron uit staat en N2 is als de bron aan staat. Het ruisgetal wordt dan gegeven door:
NF = ENR - 10 log (N2/N1 - 1) dB (6)
N2/N1 moet men in deze formule niet in decibels invullen. Is de verhouding in dB gemeten, dan moet het eerst worden omgezet in een niet-logaritmische maat.
Voorbeeld:
Stel dat we een bron hebben met een ENR van 6 dB en dat aan de uitgang een vermogensverhouding van 3,5 dB is gemeten. Wat is het ruisgetal van de ontvanger?
Oplossing:
De verhouding N2/N1 = 10(V/10) met V als de verhouding in dB. Invullen levert N2/N1 = 2,24. Dit weer in formule (6) invullen:
NF = 6 - 10 log (2,24 - 1) = 5,1 dB.
Veelal wordt de verhouding N2/N1 aangeduid als de Y-faktor; deze meet men aan de uitgang van de ontvanger. Meet men bijvoorbeeld zonneruis, in verhouding tot de "koude" hemel, dan vindt men voor Y feitelijk:
Y = (S+N)/N.
Deze methode van meten beet wel de "warm-koud methode", omdat men met een bron werkt die twee vastgestelde ternperaturen heeft. Is Trx de ontvangertemperatuur, Tw de temperatuur van een warme weerstand en Tk die van een koude weer-stand aan de ingang van de ontvanger, dan geldt voor Y:

en dus geldt:
![]()
Als er voor Tkoud de standaardtemperatuur TO wordt gekozen en voor Twarm de brontemperatuur Taan wordt ingevuld, en men dan formule (8) in formule (4) invult, dan ontstaat tenslotte formule (6).
6. De systeemtemperatuur
Een veel voorkomend probleem is de serie schakeling van een aantal tweepoorten waarvan de ruisgetallen of ruistemperaturen bekend zijn. In hoeverre namelijk wordt het ruisgetal gedomineerd door de eerste trap?
Figuur 2 last een serie schakeling zien van twee apparaten, bijvoorbeeld een voorversterker en een ontvanger, die allebei ruis opwekken. Van beide trappen is bekend wat de equivalente ruistemperatuur is en van de eerste trap weet men bovendien de vermogensversterking G1.

Fig. 2. Twee ruisende tweepoorten in serie, voorgesteld als ruisvrije tweepoorten met equivalente ruisbronnen aan de ingang.
De ruisbron van de tweede trap staat tussen de eerste en de tweede trap in. Plaatst men nu deze bron N2 aan de ingang van de eerste trap, dan wordt deze bron met een faktor G1 verkleind:
N2ingang = N2/G1 (9)
Er is al een ingangsbron met vermogen N1 (de ruis van de eerste trap) en de totale ruis aan de ingang heeft dan een vermogen:
N = N1 + N2ingang = N1 + N2/G1 (10)
Zijn nu T1 en T2 de ruistemperaturen van trap 1 resp. trap 2, dan is de totale ruistemperatuur:
Tsyst = T1 + T2/G1 (11)
Voorbeeld:
We hebben een voorversterker met een vermogensversterking van 13 dB en een ruisgetal van 1 dB. De ontvanger erachter heeft een ruisgetal van 5 dB. Wat is de systeemtemperatuur?
Oplossing:
Eerst moeten de ruistemperaturen van de twee apparaten berekend worden.
Voorversterker: NF = 10 log (T1 /TO + 1) waaruit volgt dat T1 = TO (10(NF/10) - 1) invullen van TO = 290 en NF = 1 geeft T1 = 75 K;
Ontvanger: invullen van NF = 5 levert T2 = 627 K.
De systeemtemperatuur is dan: (met formule 11)
Tsyst = 75 + 627/20 = 106 K (13 dB ≡ 20 maal)
Heeft men M trappen in serie staan dan is de systeemtemperatuur:

Deze serieschakeling is in figuur 3 getekend.

Fig. 3. M tweepoorten in serie
Wordt er een verzwakker gebruikt in plaats van een versterker, dan is de versterking dus kleiner dan een. Is D de dempingsfaktor dan is de versterking G gelijk aan:
G = 1/D (13)
De verzwakker heeft ook nog een inwendige weerstand, die ruis opwekt. De ruistemperatuur van een verzwakker hangt of van de dempingsfaktor:
T = (D - 1)Tomgeving (14)
Tomgeving is de werkelijke temperatuur van de kabel. Hangt de kabel buiten en is de buitentemperatuur b.v. 13 graden celcius dan is deze Tomg. dus 273 + 13 = 286 K.
Deel 1 - deel 2.
PE1CUX.