Rekenen met ruisgetal en ruistemperatuur 2
Na al deze theorie volgt nog een praktisch voorbeeld. Beschouw de schakeling van figuur 4A. De antenne is met een coaxkabel (met verlies) aan een voorversterker verbonden. De voorversterker staat direkt voor de ontvanger.
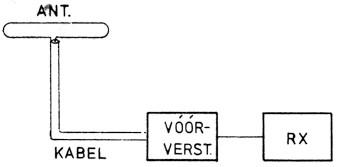
Fig. 4A.
In figuur 4B is de coax tussen de voorversterker en de ontvanger gemonteerd. Het is nu de bedoeling om de verbetering te berekenen die verkregen is door de voorversterker boven in de mast te plaatsen.
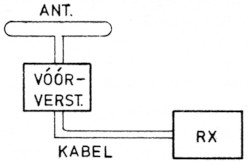
Fig. 4B. Verbetering van het ruisgetal door vermindering van de kabelruis en kabeldemping
Stel, dat de NF van de voorversterker 1 dB is, de demping van de coax 2 dB bedraagt, de NF van de ontvanger 3 dB is en voorts is de temperatuur 17° C. De SWR is 1:1 en de vermogensversterking van de voorversterker bedraagt 13 dB. De antenne is verliesloos, zodat die zelf niet ruist.
Voor de schakeling van figuur 4A wordt nu de systeemtemperatuur berekend.
Ddb = 2 dB, zodat D = 1,585 en Tkabel = (1,585 - 1) 290 = 170 K.
Voorversterker: NF = 1 dB, dus T1 = 75 K; G1 = 13 dB = 20 maal.
Ontvanger: NF = 3 dB waaruit volgt dat T2 = 290 K.
Deze waarden invullen in formule (12) met M = 3:
Tsyst = Tkabel + T1 /Gkabel + T2/GkabelGl = 170 + 1,585 × 75 + 1,585 × 290/20 = 312 Kelvin.
Voor schakeling van figuur 4B wordt formule (12) als volgt ingevuld:
Tsyst = T1 + Tkabel/G1 + T2/GkabelG1.
De kabeltemperatuur wordt dus met een faktor G1 verkleind!
Tsyst = 75 + 170/20 + 1,585 × 290/20 = 106 Kelvin.
De temperatuur is dus bijna drie maal zo klein geworden. Er is dan 10 log(Ta/Tb) 4,7 dB minder signaalvermogen nodig in schakeling 4B dan in 4A voor dezelfde signaal-ruisverhouding. En niet twee decibel, zoals de kabeldemping zou suggereren!
7. De gevoeligheid van een systeem
Een ontvanger met een bepaald ruisgetal kan slechts signalen ontvangen die sterker zijn dan de ruis. We kunnen bij het ruisgetal een equivalente ruistemperatuur berekenen en dan is ook het ruisvermogen van de ontvanger bekend:
Nrx = kTB (k = 1.38 × 10-23 J/K) (2)
Laten we nu eens het ruisvermogen van een ontvanger berekenen als de ruistemperatuur 75 Kelvin is (NF = 1 dB). Voor een CW signaal kunnen we volstaan met een erg smal filter, b.v. met een bandbreedte B = 50 Hz. Dan is Nrx:
Nrx = 50 × 75 × 1,38 × 10-23 = 5,18 × 10-20 watt.
Dit komt overeen met een vermogen van -162,9 dBm (dB ten opzichte van een milliwatt). Voor een redelijke neembaarheid moet de Y faktor in de orde van 4 liggen [(S+N)/N is 6 dB]. Dan is S drie maal zo groot als N, ofwel 4,8 dB. Dan kunnen dus met het bovenstaande systeem signalen worden ontvangen met een vermogen van -162,9 + 4,8 = -158,1 dBm.
Kiezen we een breed filter, b.v. voor SSB, dan wordt de grens gevoeligheid snel slechter. Met een filter van 2500 Hz breedte wordt Nrx gelijk aan -146 dBm (NF = 1 dB). Met een Y faktor van 10 is S negen maal zo groot als N, ofwel 9,5 dB.
Voor een (S+N)/N verhouding van 10 dB moet het signaalvermogen -146 + 9,5 = -137,5 dBm bedragen.
In praktijk hebben we nog extra problemen, die de ontvangstgevoeligheid slechter maken. De antenne kan ruis van de aarde, de zon of van de melkweg oppikken en een slechte SWR kan een deel van het signaal laten verdwijnen.
De aardruis in het bijzonder beperkt de gevoeligheid voor signalen die over de oppervlakte komen. Dit kan men als volgt zien: de aarde is "warm" en straalt dus thermische ruis uit. De antenne staat horizontaal, b.v. voor tropo verbindingen, en de hoofdlob van de antenne ziet dus voor de helft de hemel boven de horizon en voor de andere helft de aarde (onder de horizon). De resulterende ruis is dan ongeveer die van de aarde met de halve waarde van de werkelijke temperatuur. Is b.v. de aarde 290 Kelvin (17° C) dan is de schijnbare temperatuur op de antenne gelijk aan 290/2 ≡ 150 K. Heeft men een systeem met een temperatuur van b.v. 75 K dan is de totale ruis gelijk aan de ruis van de antenne plus de eigenruis en dit levert dan een ruistemperatuur op van 75 + 150 = 225 K. Een signaal moet dus meer vermogen hebben dan deze totale ruis (aardruis + systeemruis).
Voorbeeld: een signaal dat 10 dB (S+N)/N moet hebben, bij een bandbreedte van 2500 Hz, moet drie maal sterker zijn dan in het vorige voorbeeld waarin de ruistemperatuur 75 K bedroeg. (Immers 225/75 = 3 maal grotere ruistemperatuur.) Een faktor 3 in vermogen is 4,8 dB, dus het signaalvermogen wordt dan gelijk aan -137,5 dBm + 4,8 dB = -132,7 dBm.
Het tweede belangrijke punt dat vaak vergeten wordt is de staande-golfverhouding. Een slechte staande-golfverhouding betekent dat het signaal niet geheel wordt overgedragen aan de ontvanger; een deel wordt gereflekteerd naar de bron. Deze "SWR" kan men opvatten als een extra dempingsweerstand die echter zelf niet ruist. Een goed aangepaste schakeling neemt alle vermogen op, dus het verlies is nul en de SWR is 1:1. Een open of kortgesloten kabeleinde heeft echter een SWR van "oneindig" staat tot 1, omdat alle vermogen wordt gereflekteerd. Er geldt het volgende verband tussen het inkomende vermogen Pin en het gereflekteerde vermogen Prefl:![]()
Het gedeelte van het vermogen dat wordt doorgegeven is:
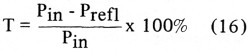
Men kan dan een verlies stellen van:
![]()
Een aantal waarden voor Tlog zijn in tabel 1 gezet.
| SWR:1 | Tlog dB |
|---|---|
| 1,1 | 0,01 |
| 1,2 | 0,036 |
| 1,5 | 0,18 |
| 2 | 0,51 |
| 3 | 1,2 |
| 4 | 1,9 |
| 5 | 2,6 |
| 10 | 4,8 |
| 20 | 7,4 |
Hieruit blijkt dat de verliezen t.g.v. SWR beperkt zijn zolang de SWR kleiner is dan 2:1. Heeft men nu een systeem met een temperatuur van 75 K, een bandbreedte van 2500 Hz en wil men een (S+N)/N van 10 dB, dan was het signaalvermogen dus -137,5 dBm. Heeft men een SWR van 5:1 op de ingang van de voorversterker dan is het verlies 2,6 dB zodat het signaalvermogen -135,1 dBm moet zijn.
Deel 1 - deel 2.
PE1CUX.