Die Anpassung der Antenne ans Kabel durch L-Glieder
Das Kabel liefert die Energie des Senders an die Antenne. Damit die Energie ohne Hindernisse in die Antenne fließt, ist es notwendig, den Wellenwiderstand am Anschluss der Antenne genau so groß zu machen wie den Wellenwiderstand des Kabels. Hier liegt der Hase im Pfeffer: In den meisten Fallen namlich stimmen die beiden nicht überein!
Der leidgeprtifte Funkamateur lasst sich nicht ins Bockshom jagen, kauft sich einen Antennenkoppler mit dem sinnigen Namen "Tuner", was "Abstimmer" heißt. Jeder halbwegs HFGebildete wei13, dass man eine Antenne gar nicht abstimmen kann. Die Resonanzfrequenz einer Antenne liegt bekanntlich fest und lasst sich durch nichts in der Welt von der Speisung her verandem, abstinunen oder "tunen". Also nimmt unser Funkfreund einen Antennenkoppler und schleift diesen zwischen Kabelende und Antennenanschluss ein. Nach professionellem Drehen an einigen Knopfen sinkt der Rücklauf-Zeiger des SWR-Meters in schauerliche Tiefen und das hehre Ziel ist erreicht: Die Welligkeit auf dem Kabel ist s = 1. Der Tuner hat beide Wellenwiderstande einander angepasst. Dummerweise wird das SWR-Meter meistens zwischen Transceiver und Kabel eingeschleift und so das SWR am falschen Ende des Kabels gemessen. Diese Methode misst das SWR zu niedrig und zu günstig, weil es durch die unvermeidliche Kabeldampfung geringer geworden ist. Freilich ist es viel bequemer, das SWR in der Funkbude zu messen als draul3en am Speisepunkt der Antenne.
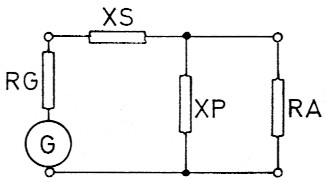
Bild 1: Das aufwarts transformierende L-Glied.
So gut wie alle Probleme der Anpassung lassen sich mit L-Gliedern Risen. Wir tinterscheiden dabei zwei Typen:
- Das Aufwarts-L-Glied passt von niedriger Impedanz auf hohe Impedanz an. Es transformiert aufwarts.
- Das Abwarts-L-Glied tut es umgekehrt, es transformiert von hoher Impedanz auf niedrige Impedanz, also abwarts.
Das Aufwarts-L-Glied
Bei diesem L-Glied liegt der Verbraucher (Antenne = A) mit seinem Wirkwiderstand RA parallel zu einem Blindwiderstand im Parallelzweig XP (Bild 1). Dabei bedeutet X = Blindwiderstand, P = parallel. In Reihe dazu liegt der Blindwiderstand des Serienzweiges XS: X = Blindwiderstand, S = Serie. Wenn XS durch eine Spule dargestellt wird, müssen wir für XP einen Kondensator wahlen und umgekehrt. Spater wird dies für die Spule plus (+) und für den Kondensator minus (-) ergeben. Es gibt also für das L-Glied zwei zueinander duale Moglichkeiten:
| XS | XP | |
|---|---|---|
| 1 | Spule L | Kondensator C |
| 2 | Kondensator C | Spule L |
Als Schlaukopfe legen wir die Spule L in den Serienzweig XS und den Kondensator C in den Parallelzweig XP. Damit haben wir einen Tiefpass geschaffen, der die Oberwellen gut dampft. Die andere Schaltung mit dem Kondensator C im Serienzweig und der Spule L im Parallelzweig ware ein Hochpass. Der Tiefpass hat die günstige Eigenschaft, Oberwellen zu unterdrücken, wahrend der Hochpass die Oberwellen nahezu ungedampft durchlasst, dagegen die tiefen Frequenzen unterdrückt. Wir werden uns deswegen bier nur mit den Tiefpass-Schaltungen beschaftigen.
Der Transceiver ist unser Generator (G). Er hat einen Innenwiderstand RG, meist 50 Ohm, was mit dem Wellenwiderstand des Kabels fthereinstimmt. Somit sind beide aneinander angepasst. Die Blindwiderstande des L-Gliedes lassen sich leicht berechnen, und wir erhalten nach (1):
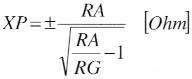
Die Güte des Aufwarts-L-Gliedes ist:
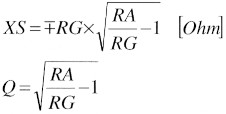
Nahezu ohne Ausnahme sind Generatorund Kabelwiderstand RG = 50 Ohm. Wir setzen in die Formel ein: RG = 50 Ohm, womit eine weitere Vereinfachung eintritt. Wird nun das Ganze mathematisch bearbeitet, womit wir unsere Leser verschonen wollen, so ergibt sich für den Blindwiderstand des Serienzweiges XS das folgende Diagramm von Bild 2. Fur den Blindwiderstand des Parallelzweiges XP ergibt sich das Diagramm von Bild 3. Aus beiden Diagrammen konnen wir mühelos die notwendigen Blindwiderstande des L-Gliedes ablesen. Dazu nun ein paar Beispiele:
- Es soll von 50 Ohm auf 100 Ohm transformiert werden. Wir lesen in Bild 2 ab: XS = 50 Ohm. Aus Bild 3 entnehmen wir XP = 100 Ohm.
- Es soll von 50 Ohm auf 800 Ohm transformiert werden. Aus Bild 2: XS = 193 Ohm. Aus Bild 3: XP = 206 Ohm.
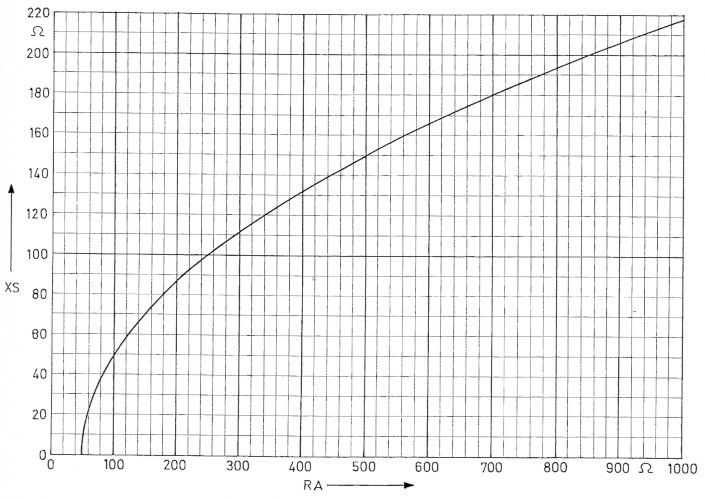
Bild 2: Der Serien-Blindwiderstand XS für Aufwarts-L-Glieder.
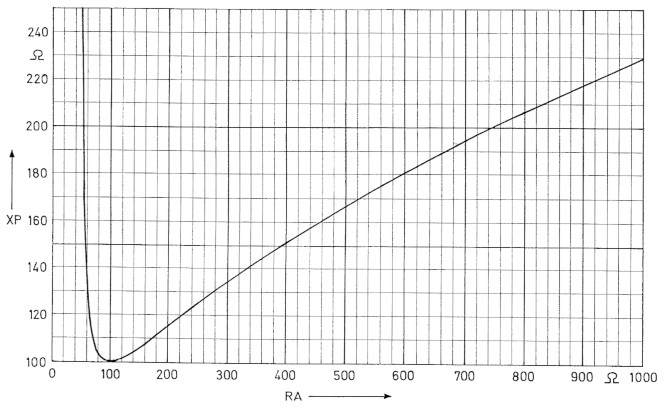
Bild 3: Der Parallel-Blindwiderstand XP für Aufwarts-L-Glieder.
Die elektrische Gri5Be der Bauteile richtet sich nach der Frequenz; denn die L-Glieder wirken nur fdr eine Frequenz und mit geringen Einschrankungen fir ein Frequenzband.
Bekanntlich ist XL = 2π × f × L. Dies ergibt für die Induktivitat:
L = XL / (2π × f)[H]. Es ist auch XC = 1 / (2π × f × C). Daraus ergibt sich die Kapazitat: C = 1 / (XC × 2π x f)[F].
Nehmen wir das erste Beispiel und rechnen jetzt für die Mitte des 80-m-Bandes, dann ist f= 3,650 MHz oder 3,65 × 106 Hz. XS war 50 Ohm. Wir verwenden dafür eine Spule, um einen Tiefpass zu haben. Also XL = XS = 50 Ohm. L = 50 / (2 × 3,142 × 3,65 × 106) [H]. L = 2,18 × 10-6 H; L = 2,18 µH. XP war 100 Ohm. Wir müssen dafür einen Kondensator nehmen, also XC = XP = 100 Ohm. Es ergibt sich: C = 1 / (100 × 2 × 3,142 × 3,65 × 106) [F]; C = 436 × 10-12 F; C = 436 pF. Das Ergebnis ist in Bild 4 zu sehen.
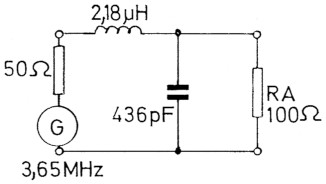
Bild 4: L-Glied nach Beispiel 1.
Für das zweite Beispiel soil die Arbeitsfrequenz 28,5 MHz sein. Also f = 28,5 MHz = 28,5 × 106 Hz. XL = XS = 193 Ohm. Damit ergibt sich die Induktivität:
L = 193 / (2 × 3,142 × 28,5 × 106) [H]; L = 1,078 µH. Im Parallelzweig ist XP = 206 Ohm. Wir müssen einen Kondensator nehmen: XC = XP = 206 Ohm. C = 1 / (2 × 3,142 × 28,5 × 106 × 206) [F]. C = 27 pF. Die gesamte Schaltung zeigt Bild 5.
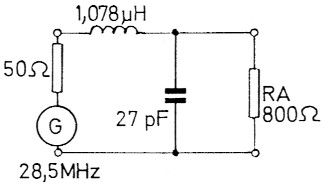
Bild 5: L-Glied nach Beispiel 2.
Und gleich noch eine Warnung: Wenn wir beide Bauteile des L-Gliedes als Parallelkreis zusammenschalten, so ist die Resonanzfrequenz nicht die Arbeitsfrequenz, für die wir das L-Glied berechnet haben. Dies gilt für beide L-Glieder, für das Aufwarts- und das Abwarts-Glied.
Wir betrachten Bild 3 genau und entdecken eine seltsame Eigentümlichkeit. Bei RA = 100 Ohm wird XP =100 Ohm. Dort hat die Kurve ein Minimum. Vom Minimum nach links oben und nach rechts oben erstreckt sich je ein Ast. Legen wir z.B. XP = 150 Ohm fest, so kann RA zwei Werte annehmen, einmal 58 Ohm, aber auch 390 Ohm. Das heil3t, mit dem gleichen XP lassen sich zwei vollig unter schiedliche Widerstande RA anpassen. Dies erklart es, dass wir manchmal den Drehko eines Antennenkopplers nicht verstellen milssen und trotzdem zwei verschiedene Antennen mit verschiedenen RAs anpassen konnen. Allerdings wird es uns nicht erspart bleiben, an der Rollspule rollen zu müssen. Diese Zweigleisigkeit ist eine Besonderheit des L-Gliedes.
Das Abwarts-L-Glied
Zur Widerstandstransformation vom Wider-stand des Kabels auf den niedrigeren der Antenne dient das Abwarts-L-Glied. Wir klappen ein Aufwats-L-Glied each links um und erhalten damit das Abwarts-L-Glied von Bild 6. Links liegt wieder der Generator mit seinem Innenwiderstand RG, parallel daze der Blindwiderstand XP und in Langsrichtung in Serie der Blindwiderstand XS. Der Antennenwiderstand RA, ganz rechts, wird damit angepasst. Um die Oberwellen zu dampfen, leggin wir wieder die Spule in den Serienzweig und den Kondensator in den Parallelzweig. Damit schaffen wir einen Tiefpass.
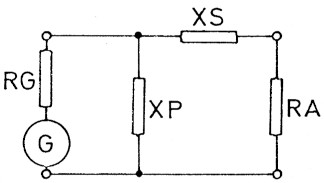
Bild 6: Das abwürts transformierende L-Glied.
Nach (1) werden die Blindwiderstande wie folgt berechnet:
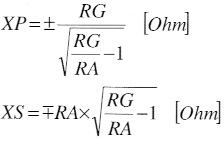
Die Güte des Abwarts-L-Gliedes ist:
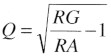
Damit vereinfacht sich alles auf:
XP = RG/Q
XS = RA × Q
Dieses Q ist nicht identisch mit dem Q des Aufwartsgliedes. Jetzt setzen wir noch RG = 50 Ohm und erhalten für den parallel liegenden Blindwiderstand XP das Diagramm von Bild 7. Der Antennenwiderstand RA ist auf der waagerechten X-Achse abgetragen. Er kann Werte von 0 bis 50 Ohm annehmen. Der parallele Blindwiderstand XP ist auf der senkrechten Y-Achse im logarithmischen Mal3stab dargestellt. Um als Tiefpass zu wirken, wird XP durch einen Kondensator realisiert.
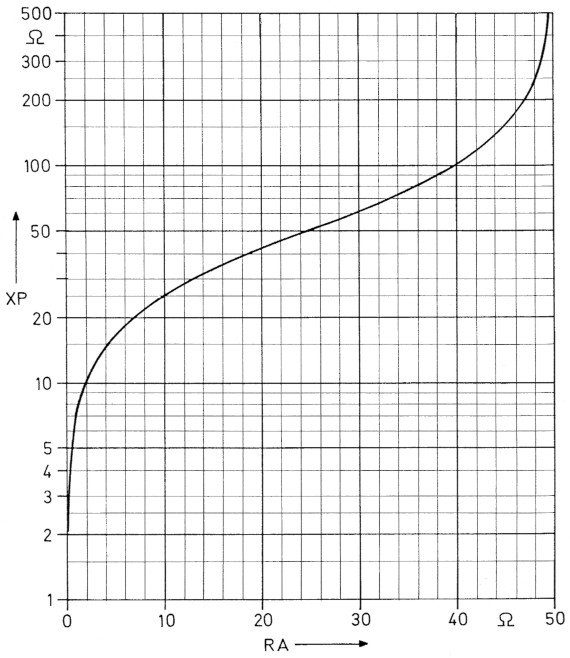
Bild 7: Der Parallel-Blindwiderstand XP für Abwarts-L-Glieder.
Jetzt wird es ein bisschen paradox: Um ein niedriges RA anzupassen, brauchen wir ein niedriges XP. Beispiel: Fur RA = 2 Ohm wird XP = 10 Ohm. Ein niedriges XP bedeutet aber einen grol3en Kondensator mit grol3er Kapazitat, oft tausend pF oder mehr. Um ein RA nape 50 Ohm anzupassen, brauchen wir ein hohes XP. Beispiel: RA = 48 Ohm. Dann wird XP = 250 Ohm. Die hohe Impedanz bedeutet einen kleinen Kondensator mit wenigen pF.
Den Serien-Blindwiderstand XS konnen wir aus dem Diagramm von Bild 8 entnehmen. Bei RA = 25 Ohm hat XS sein Maximum mit 25 Ohm. Vom Maximum fallt die elliptische Kurve nach links und rechts in zwei Zweigen nach Null ab. Damit ist wieder eine Zweideutigkeit geschaffen. Mit einem XS von 10 Ohm konnen wir sowohl RA = 2 Ohm als auch RA = 48 Ohm anpassen. Mit XS = 20 Ohm lassen sich RA = 10 Ohm und RA = 40 Ohm anpassen.
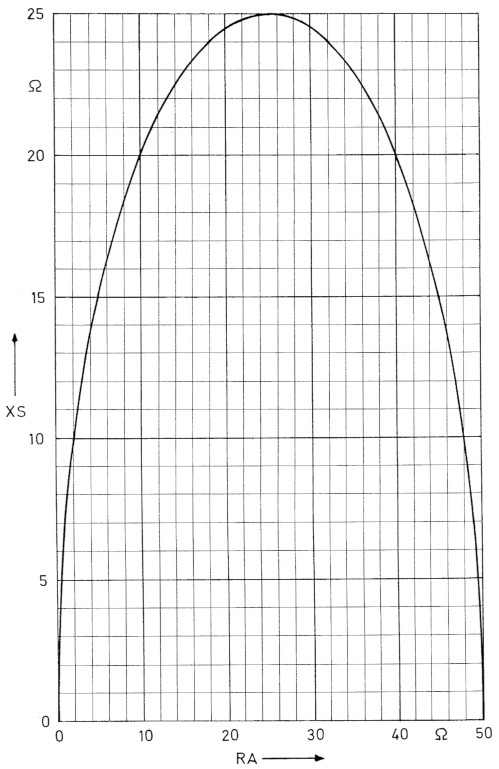
Bild 8: Der Serien-Blindwiderstand XS für Abwarts-L-Glieder.
Aus den beiden Diagrammen lassen sich die GroBen der Bauteile eines Abwarts-LGliedes bequem bestimmen. Dazu die folgenden Beispiele:
RA = 35 Ohm; f = 7 MHz. Wir finden XP mit 76 Ohm auf Bild 7. Im Diagramm Bild 8 ergibt sich XS mit 23 Ohm. Weil XP ein Kondensator ist, wird seine Kapazitat C = 1 / (2π × f × XC); C = 1 / (2 × 3,142 × 7 × 76 × 106) [F]. C = 299 pF. XS ist eine Spule mit der Induktivitat L. L = XS / (2π × f). L = 23 / (2 × 3,142 × 7 × 106) [H]. L = 0,52 µH. Bild 9 zeigt die Schaltung.
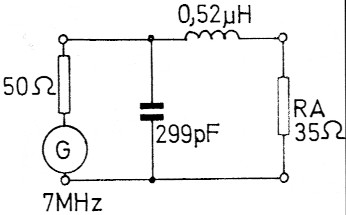
Bild 9: L-Glied nach Beispiel 3.
RA = 8 Ohm; f = 1,835 MHz. Im Diagramm Bild 7 finden wir XP = 22 Ohm; in Bild 8 ist XS = 18,4 Ohm. XP soll ein C sein. C = 1 / (2π × f × XC); C = 1 / (2 × 3,142 × 1,835 × 22 × 106) [F]; C = 3,942 nF. XS soll ein L sein. L = XL / (2π × f); L = 18,4 / (2 × 3,142 × 1,835 × 106) [H]; L = 1,596 µH. Bild 10 demonstriert das Schaltbild.
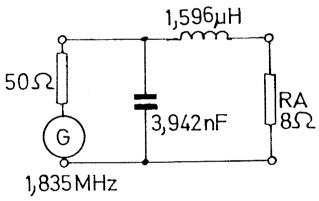
Bild 10: L-Glied nach Beispiel 4.
Wer sich die Mühe gemacht hat, die Impedanzen der Schaltglieder mit Hilfe der oben angeführten Formeln gerechnet zu haben, der wird feststellen, dass die Werte der Rechnung von den aus den Diagrammen entnommenen Werten geringfügig abweichen, um Bruchteile eines µH oder urn einige pF. Wir haben die bequeme Entnahme aus den Diagrammen mit ein bisschen Genauigkeit bezahlt. Beim Aufbau des L-Gliedes in der Praxis spielt dies keine Rolle; denn wir konnen unsere Spulen oder Kondensatoren auch nicht genau herstellen und Sind nach dem Aufbau zum Abgleich gezwungen. Die Genauigkeit der Arbeit mit Diagrammen reicht also für die Praxis vollig aus. Wer besonders bequem ist, kann für die Bestimmung von L und C eine so genannte "HF-Tapete" verwenden, die natlirlich auch nicht recht genau ist.
Die Antenne ist kein reiner Wirkwiderstand
Wenn die Antenne in Resonanz schwingt, bietet sie dem Kabel immer einen reinen Wirkwiderstand, rein ohmisch, ohne kapazitive oder induktive Komponente. Strahlt die Antenne auBerhalb ihrer Resonanz, dann ist an ihrem Anschluss aul3er dem Wirkwiderstand noch ein Blindwiderstand festzustellen. Liegt die Speisefrequenz fiber der Resonanzfrequenz, dann kommt ein induktiver Blindanteil dazu.
Liegt die Speisefrequenz unter der Resonanzfrequenz, dann kommt ein kapazitiver Blindanteil dazu. Weil eine Antenne auch in Oberwellen erregt werden kann, gilt dies jedoch nicht, wenn beide Frequenzen sehr weft auseinander liegen.
Wir brauchen vor dem Blindanteil keine Angst zu haben. Er lasst sich mit einem Trick beseitigen, und dieser Trick heißt: Kompensation. Wir sehen in Bild 11 eine Antenne, die an ihren Klemmen Wirkwiderstand RA und Blindwiderstand XA aufweist. Der storende, kapazitive Anteil wird kompensiert. Wir erinnern uns, dass Kapazitat und Induktivitat exakt gegeneinander wirken. Urn die storende Kapazitat zu beseitigen, müssen wir nur eine Induktivitat in Reihe schalten, die den gleichen Blindwiderstand hat, also: XL = -XA Das Minuszeichen bedeutet, es lasst sich nur mit dem Gegenteil kompensieren, also L gegen C oder C gegen L. Im allgemeinen ist die kompensierende Induktivitat ein kleines Spillchen. Als bequeme Leute machen wir die bereits vorhandene Spule von XS urn den notwendigen Betrag groBer, und die Sache ist erledigt.
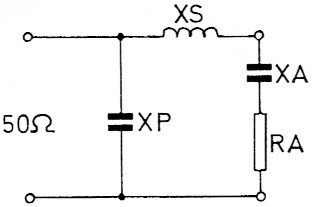
Bild 11: Die Antenne hat eine kapazitive Komponente XA.
Bild 12 zeigt eine Abwartstransformation, bei der die Antenne induktiv belastet ist. Wir ahnen schon, was jetzt kommt: Theoretisch müssten wir einen Kondensator dort in Reihe schalten, urn die Induktivitat herabzusetzen. Da aber XS und XA in Reihe geschaltet sind, verkleinem wir die Spule von XS urn die GraBe von XA und haben unser Ziel erreicht. Die beiden letzten Rile konnten kompensiert werden, ohne weitere Bauteile zu verwenden. Dies ist bei der Aufwartstransformation leider nicht moglich. Der Griffin die Bastelkiste ist nicht zu vermeiden.
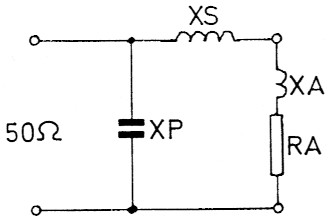
Bild 12: Die Antenne hat eine induktive Komponente XA.
Auf Bild 13 stehen an den Antennenldemmen Wirkwiderstand RA und kapazitiver Anteil XA. Wir wickeln ein Spillchen, dessen XL so groß ist wie das XC der kapazitiven Komponente, schalten Xkomp in Reihe und das lastige XA ist kompensiert. Bei Bild 14 ist der Blindanteil induktiv. Er muss kapazitiv kompensiert werden. Dazu schalten wir einen Kondensator in Reihe. Sein Blindwiderstand XC = Xkomp muss so groB sein wie XA des induktiven Anteils.
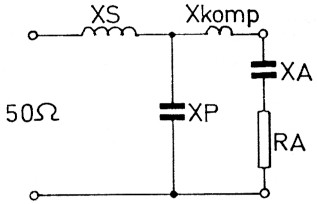
Bild 13: Xkomp kompensiert das kapazitive XA.
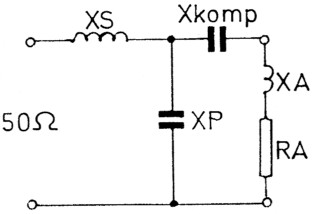
Bild 14: Xkomp kompensiert das induktive XA.
Zum Schluss noch etwas für den Praktiker. Es ist nicht immer sofort zu sehen, ob ein L-Glied den Wirkwiderstand aufwarts oder abwarts transformiert. Dazu erinnern wir uns, class der Serienschwingkreis eine sehr niedrige Impedanz hat: Z ist klein. Die Elemente des Serienschwingkreises haben jedoch eine sehr hohe Impedanz: Z ist groß. Bild 15 zeigt uns eine Aufwarts-Transformation von den Klemmen des Serienkreises zu den Klemmen des Kondensators. Bild 16 demonstriert eine Abwarts-Transformation vom Kondensator zum Serienkreis. Wenn wir uns das einmal klar gemacht haben, ist das nie mehr zu vergessen. Als Ubung konnen wir uns die Bilder 1/4/5/6/9/10 und 11 bis 14 anschauen und bestimmen, um welche Transformation es sich handelt: auf oder ab?
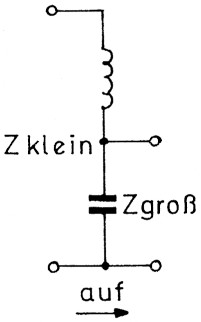
Bild 15: Serienschwingkreis und Aufwartstransformation.
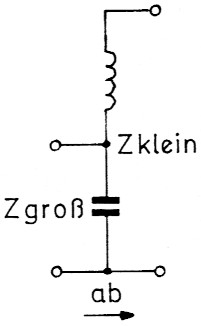
Bild 16: Serienschwingkreis und Abweirtstransfor:nation.
Literatur und Quellen
DL1VU, Karl H. Hille.