Die Strahlung von Langdrahtantennen und ihre Nullwinkel
Langdrahtantennen sind einfach, billig, schnell aufzuhangen und trotz ihrer simplen Konstruktion sehr wirkungsvoll. Daher sind Langdrahte such auBerordentlich haufig anzutreffen. Besonders auf den niederen Bandern tun sie gute Dienste. Aber nicht jeder 20-m-Draht, der im Garten baumelt, ist schon eine Langdrahtantenne. Es gehort schon ein bisschen mehr dazu! Leider ist in den Ietzten Jahrzehnten das Wissen um die Langdrahtantenne kaum gepflegt worden. Man war bequem geworden und hatte auch seine Aufmerksamkeit mehr auf spektakulare Antennenformen gerichtet. Deshalb sollen die grundlegenden Tatsachen hier offen gelegt werden. Und wie es sich bei sorgfaltiger Untersuchung ergibt, konnen wir stolz mit einigen Neuheiten aufwarten.
Wanderwellen
Eine Langdrahtantenne stellt ein Beispiel fir eine Wanderwellenantenne dar. Die Bezeichnung "Langdraht" meint einen geraden Leiter mit einer Lange von einer bis zu vielen Wellenlangen. Kürzere Drahte bis zu etwa werden fast immer in Stehwellen erregt, wenn wir nicht besondere Anstalten vorsehen, sie in den Wanderwellenmodus zu bringen. Es ist bekannt, dass die stromuihrenden Halbwellen-Abschnitte Antennencharakteristiken hervorrufen, die in eine Anzahl von Strahlungskeulen gespalten sind. Die Zahl dieser Keulen wachst mit der Lange der Antenne an. Zwischen den Keulen liegen scharfe Nullstellen ohne Strahlung. Im dreidimensionalen Raum entpuppen sich die Keulen als fleischige Trichter, die axial urn die Drahtachse der Langdrahtantenne angeordnet sind. Bild 1 gibt einen Eindruck davon. Wenn in Folge hier von Keulen die Rede ist, so haben wir damit stets den Schnitt durch den Drehkorper im Auge, und wissen genau, dass es raumliche Trichterkorper sind.
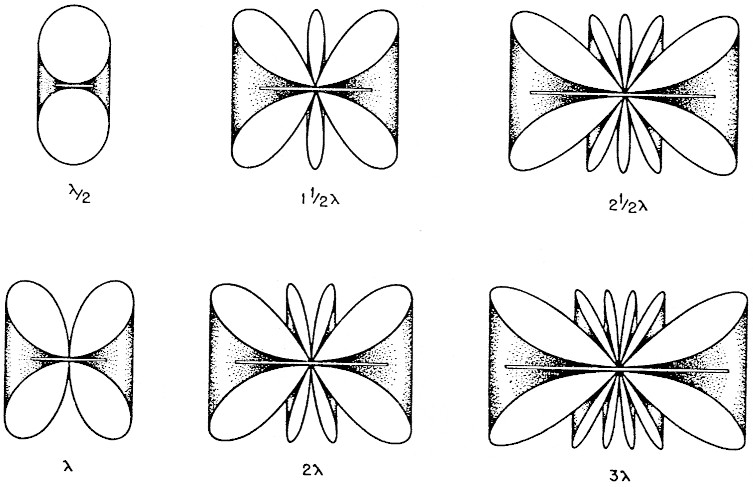
Bild 1: Haupt- und Nebenkeulen und die trichterformigen Antennencharakteristiken.
Die Verteilung der abgestrahlten Energie urn eine Langdrahtantenne in Erregung mit einer Wanderwelle wird durch den Formfaktor FΘ beschrieben, den wir auch Polarkoeffizient nennen konnen.(1)
FΘ = sin (πL × (1 - cos Θ)) × sin Θ/(1 - cos Θ) [1]
Θ = Winkel zwischen dem abgestrahlten Feld und der Drahtachse
L = Lange des Drahtes, gemessen in λ.
Nullstellen der Strahlung
Wie schon Bild 1 zeigt, treten die Nullstellen bei bestimmten Winkeln auf. Mathematisch sind dies Nullstellen einer Funktion. Physikalisch sind es Winkel ohne Strahlung, die wir Nullwinkel nennen wollen. Die Nullwinkel der Strahlung zu finden ist recht einfach. Wir müssen nur [1] gleich Null setzen:
FΘ = 0. Da eroffnen sich sofort drei Moglichkeiten:
1. sin Θ = 0; das bedeutet Θ = 0 mit dem Ergebnis: In Richtung der Drahtachse gibt es keine Strahlung.
2. Wenn sin Θ nicht Null ist, muss der erste Teil der Gleichung [1] Null sein.
sin (πL × (1 - cos Θ) = 0
πL × (1 - cos Θ) = 0
1 - cos Θ = 0
cos Θ = 1
Θ = 0
Das Ergebnis ist das gleiche wie in 1.
3. Es ist wohl bekannt: Die Sinuskurve schneidet die X-Achse bei den in Radiant gemessenen Winkeln 0 = π, 2π, 3π, ... Dort ist sin π = 0 und dies ergibt far den ersten Teil von [1]:
πL × (1 - cos Θ) = π
L × (1 - cos Θ) = 1
1 - cos Θ = 1/L
cos Θ = 1 - 1/L
Diese Formel ist natarlich mehrfach gültig für: λ, 2λ, 3λ, wir bekommen also:
cos Θ = 1 - n/L; n = 0; 1; 2; 3; ...
Nullwinkel fur Drahte mit Wanderwellen
Θ = cos-1 (1 - n/L) [2]
L= Lange des Drahtes in λ, n = 0; 1; 2; 3; ...
Als praktisches Beispiel wahlen wir einen Draht von der Lange 2λ. Die Nullwinkel fur Θ sind:
Θ0 = cos-1 (1 - 0/2);
Θ1 = cos-1 (1 - 1/2);
Θ2 = cos-1 (1 - 2/2);
Θ3 = cos-1 (1 - 3/2);
Θ4 = cos-1 (1 - 4/2).
Werte großer als |1| sind für den Cosinus nicht moglich. Der Taschenrechner quittiert so etwas mit "error"!
Die Ergebnisse sind:
Θ0 = cos-1 (1) = 0°
Θ1 = cos-1 (0.5) = 60°
Θ2 = cos-1 (0) = 90°
Θ3 = cos-1 (- 0.5) = 120°
Θ4 = cos-1 (- 1) = 180°
Zu sehen ist das auf Bild 2. Auf diese Weise berechnete Nullwinkel stimmen mit der Antennentheorie exakt überein, es sind also keine Naherungslosungen.
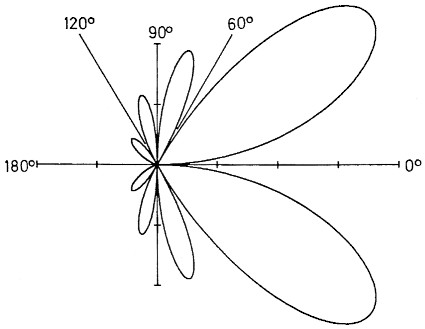
Bild 2: Nullwinkel einer 2λ Wanderwellenantenne.
Nullwinkel bei Stehwellenerregung
Wenn ein Draht verhaltnismaBig kurz ist, z. B. 1λ, bis 3λ, dann schwingt er in Stehwellen, es sei denn wir treffen besondere Mal3nahmen für eine Erregung in Wanderwellen. Der Formfaktor oder der Polarkoeffizient beschreibt die Abstrahlung and lautet(2):
FΘ = ((cos(πL × cos Θ) - cos πL) + j(sin(πL × cos Θ) - sin (πL) × cos Θ)) / sin Θ [3]
Dabei ist
L = Lange in λ
j = imaginarer Operator
Um diese Formel zu Risen, quadrieren wir den ersten Term, quadrieren den zweiten Term, addieren beide Werte und ziehen daraus die Quadratwurzel. Das Ergebnis wird noch durch sin Θ geteilt. Die Losung dieser Formel [3] für Drahtantennen, die eine gerade Anzahl von Halbwellen lang sind, erhalten wir nach langwierigen Umformungen als:
FΘ = sin (πL × cos Θ) / sin Θ
L ist eine gerade Zahl von λ/2! [4]
Fur Drahtantennen mit Langen, die eine ungerade Anzahl von Halbwellen lang sind, erhalten wir aus [3]:
FΘ = cos (πL × cos Θ) / sin Θ
L ist eine ungerade Zahl von λ/2! [5]
Ermitteln der Nullwinkel
1. Die Lange ist ein gerades Vielfaches von λ/2
In Formel [4] setzen wir: FΘ = 0. Weil sin 0 nicht großer als 1 sein kann, konnen wir schreiben:
sin (πL × cos Θ) = 0
Der Sinus ist 0 für Argumente von: 0; π; 2π; 3π; So ergibt sich:
πL × cos Θ = 0; π; 2π; 3π; ...
L × cos Θ = 0; 1; 2; 3; ...
cos Θ = 0/L; 1/L; 2/L; 3/L; ... oder
cos Θ = n/L; n = 0; 1; 2; 3; ...
Nullwinkel geradzahliger λ/2-Drahte in Stehwellenerregung:
Θ = cos-1 (n/L); n = 0; 1; 2; 3; ... [6]
L ist die Lange in λ und ein gerades Vielfaches von λ/2.
Als praktisches Beispiel wählen wir L = 1λ. L ist ein gerades Vielfaches von λ/2. Wir bekommen aus [6] für die Werte in den Klammern: n/L = 0/1 and 1/1 and 2/1. Dann sind die Nullwinkel Θ = cos-1 (0) = 90° and Θ = cos-1 (1) = 0°. Der dritte Wert "2" ergibt keinen Winkel und ist Unsinn, weil cos Θ = 2 nicht existiert. Bild 3 zeigt das Feldstarke-Diagramm mit den beiden Nullwinkeln.
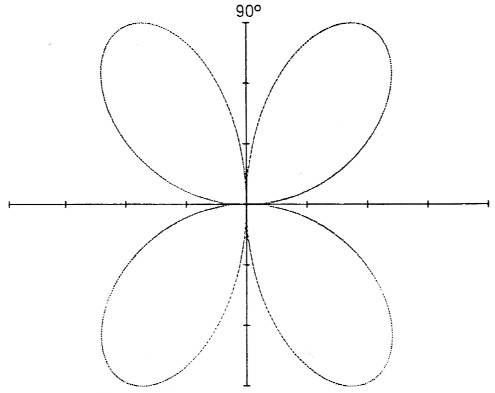
Bild 3: Nullwinkel einer 1λ-Stehwellenantenne.
1. Die Lange ist ein ungerades Vielfaches von λ/2
Wir setzen in [5] FΘ = 0 und erhalten: cos (πL × cos Θ) = 0. Der Cosinus ist 0, wenn sein Argument lautet: π/2; 3π/2; 5π/2; ... So ergibt sich:
πL × cos Θ = π/2; 3π/2; 5π/4...
L × cos Θ = 1/2; 3/2; 5/2; ...
cos Θ = 1/2L; 3/2L; 5/2L; ... oder
cos Θ = m/2L; m = 1; 3; 5; ...
Nullwinkel ungeradzahliger λ/2-Drahte in Stehwellenerregung:
Θ = cos-1 (m / (2 × L)); m = 1; 3; 5; 7; ... [7]
L ist die Lange in λ und ein ungeradzahliges Vielfaches von λ/2.
Wir wollen dies für eine Drahtantenne von L = 3,5λ anwenden und erhalten:
Θ = cos-1 (m/7)
Das ergibt folgende Argumente: m/7 = 1/7; 3/7; 5/7; 7/7. Der Bruch 9/7 ist nicht mehr brauchbar, weil er großer als 1 ist. Die dazu gehorigen Nullwinkel sind: Θ = 81,8°; 64,6°; 44,4° und Diese Winkel sind in Bild 4 zu sehen.
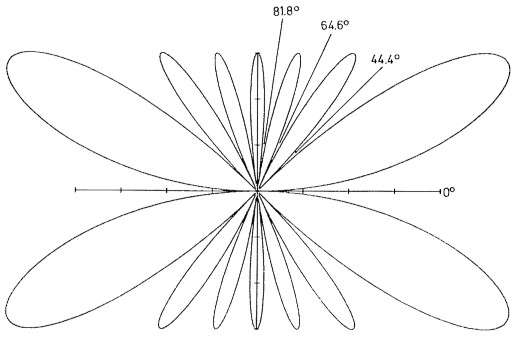
Bild 4: Nullwinkel einer 3,5 λ-Stehwellenantenne.
Neue, allgemeine Formel ffir Nullwinkel der Strahlung von durch Stehwellen oder Wanderwellen erregten Drahtantennen
Weitere Untersuchungen und Berechnungen zeigen, dass ein in Stehwellen erregter Langdraht nur Nullwinkel hat, wenn er Vielfache von λ/2 lang ist. Alle anderen Langen haben keine Nullwinkel, sondem Minima mit verminderter Strahlung. Wir sehen in Bild 5 das Diagramm der Feldstarke eines Drahtes von L = 1,75λ. Da gibt es nur einige Minima, aber keine Nullwinkel mit Ausnahme der Null in Achsrichtung. Drahte einer Lange von ungeradzahligen Vielfachen von λ/4 (also: 0,75λ, 1,25λ, 1,75λ, 2,25λ usw.)zeichnen sich durch besonders kleine Minima und sehr geringe Nebenkeulen aus. Sie sind hervorragend dazu geeignet, die Hauptstrahlung zu verstarken und die Nebenstrahlung zu unterdnicken. Eine Tatsache, die in der Antennentechnik bisher kaum Beachtung gefunden hat.
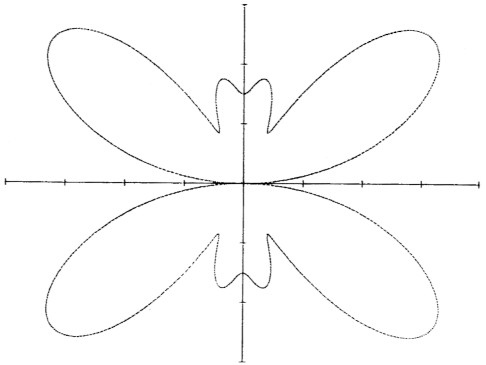
Bild 5: Feldstärkediagramm einer 1,75λ Stehwellenantenne, keine Nullwinkel!
Im Gegensatz zur Erregung in Stehwellen, hat ein in Wanderwellen erregter Draht jeder beliebigen Lange ausgepragte Nullwinkel (siehe Bild 6, L = 1,75λ). Wenn wir die Formeln [2], [6] und [7] in eine einzige, zusammenfassende Formel kombinieren, erhalten wir für alle Drahtantennen, gleichviel, ob sie in Stehwellen oder Wanderwellen erregt sind, eine allgemeine Formel.
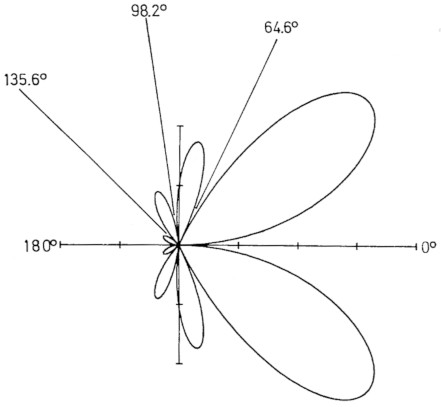
Bild 6: Feldstärkediagramm einer 1,75λ-Wanderwellenantenne, funf Nullwinkel!
Allgemeine Formel fur Nullwinkel
Θ = cos-1 (l - n / L) ; n = 0; 1; 2; 3; ...; L=Länge in m λ [8]
Achtung: Antennen mit Wanderwellen haben Nullwinkel, gleichviel wie lang sie sind. Antennen mit Stehwellen haben Nullwinkel nur bei Langen in Vielfachen von λ/2. Bei alien anderen Langen treten nur Minima auf. Die Stehwellen-Nullwinkel sind Einzelwerte (Singularitaten).
Bild 7 zeigt uns die Nullwinkel für Stehwellenantennen. Unten sind die Nullwinkel nach der ersten Keule (Hauptkeule) zusammengefasst. In der Mitte sind die Nullwinkel nach der zweiten Keule und oben der Nullwinkel nach der dritten Keule zu sehen. Die Linien zwischen den Nullwinkeln deuten nur die Zusammengehorigkeit an.
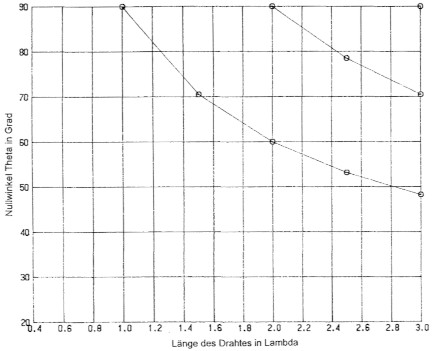
Bild 7: Die Nullwinkel von Stehwellenantennen treten als Einzelwerte nur an λ/2-Punkten auf.
Aus den bis hier erarbeiteten Grundlagen sind zwei Fakten besonders hervorzuheben: Die allgemeine Formel für Nullwinkel (neu!) und die zu einem Minimum zusammengeschrumpften Nebenkeulen bei Stehwellenantennen, wenn diese 0,75λ, 1,25λ, 1,75λ, 2,25λ usw. lang sind.
Aus solchen Elementen lassen sich für die Praxis qualitativ hoch stehende Antennen konstruieren, wie z. B. resonante Rhomboid-Antennen. Der zweite Teil dieser Arbeit wird sich mit den Maxima der Strahlung befassen und mit einigen aberraschenden Ergebnissen aufwarten konnen.
Literatur und Quellen:
- G. S. Ajsenberg, Kurzwellenantennen, Fachbuchverlag Leipzig, 1954, hier: Seite 97 ff
- a. a. 0., Seite 100 ff
DL1VU, Karl H. Hille.