Die Strahlung von langdrahtantennen und ihre Maxima
Praktische Konsequenzen für verbesserte V-Antennen
In dieser zweiten Folge lernen wir vier Methoden kennen um das Maximum der Strahlung zu ermitteln: die Phasenmethode, die Naherungslbsung, die Ermittlung durch Probieren und die elegante Berechnung unter Anwendung der numerischen Mathematik. Im Vergleich dieser unterschiedlichen Losungsansatze wird sich die zweckmaBigste und genaueste Methode herausstellen. So ganz nebenbei kommen wir auch noch zu ganz neuen Erkenntnissen!
Wanderwellen
Die Abstrahlung von einer in Wanderwellen erregten Langdrahtantenne lasst sich durch ihren Polarkoefüzienten beschreiben:
FΘ = sin (πL × (1 - cos Θ)) × sin Θ / (1 - cos Θ) [1]
Θ = Winkel zwischen der abgestrahlten Feldstarke und der Achse des Drahtes,
L = Lange des Drahtes in λ.
Wie wir schon gesehen ha-ben, hat these Strahlung Nullwinkel, aus denen nichts herauskommt und Maxima, bei denen die Strahlung ihren h6chsten Wert annimmt.
Strahlungsmaxima
Die Strahlungsmaxima zu finden ist leider nicht so einfach wie die Nullwinkel festzustellen; aber es gibt drei verschiedene, gute Wege, dies zu tun, allerdings auch mit unterschiedlichen Ergebnissen. Die einfachste, doch ungenaueste Methode ist die Phasenmethode. Wesentlich naher zum Ziel kommen wir mit der Naherungsmethode und die beste Losung ist die numerische Berechnung mit dem Computer.
1. Die Phasenmethode fur das Maximum an Strahlung
Wir kehren zu Gleichung [1] zurück. Der Faktor sin Θ / (1 - cos Θ) beschreibt im Wesentlichen die Verteilung der Feldstarke in dem Raum, der die Langdrahtantenne umgibt. Nach vorn wird mehr und nach hinter wird weniger abgestrahlt. Daher haben alle Wanderwellenantennen ein merkbares Vor-/Rückverhaltnis. Der Einfluss auf die Richtung der Strahlung ist aber nicht allzu stark. Damit konnen wir auf den zweiten Teil der Gleichung [1] verzichten. Der großte Wert, den sin x annehmen kann, ist 1. Wir können also setzen:
sin (πL (1- cos Θ)) = 1, dies bedeutet, da sin π/2 = 1 ist:
πL (1 - cos Θ) = π/2
L(1 - cos Θ)= 1/2
1 - cos Θ = 0,5/L
Um den damit berechneten Winkel des Maximums darzustellen, nehmen wir eine Drahtantenne der Lange L = 2 λ. Das erste und Haupt-maximum wird dam wie folgt berechnet:
cos Θ = (2 - 0,5) / 2
cos Θ = 1,5/2 = 0,75
Θ = cos-1 (0,75)
Θ = 41,4°
Dies ist auf Bild 1 zu sehen. Es ist offensichtlich, dass die hier vorgestellte Phasenmethode nicht besonders genau ist, der berechnete Winkel liegt merkbar neben dem Maximum.
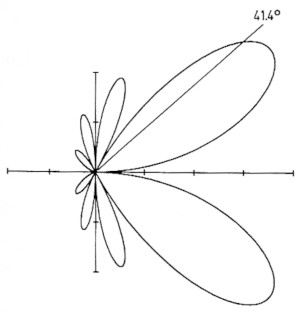
Bild 1: Diagramm einer 2-λ-Antenne und nach der Phasenmethode berechneter Winkel des Maximums.
Interessant ist, wie es zu dem Ausdruck Phasenmethode gekommen ist. Wort und Rechnungsart stammen aus der Konstruktionspraxis von Rhombusantennen. Hier soil amlich der folgende Antennenabschnitt zu dem vorhergehenden Antennenabschnitt einen Phasenunterschied von λ/2 haben. Dieses Prinzip ist in Bild 2 erklart. Hier ist nur die eine Hälfte der Rhombusantenne gezeigt. Die Pfeile zeigen die Senderichtung. Ein Antennenabschnitt ist 1 λ lang. In Senderichtung liegt der Langenunterschied d. Wenn wir Gleichung [2] anwenden, erhalten wir Θ = 60°. Dann ist L = λ und d = λ/2. In Senderichtung startet Draht Nummer 2 genau nach einer Halbwelle λ/2. Wenn wir uns Gleichung [2] anschauen, so sehen wir, dass d immer λ/2 kürzer ist als L. Nehmen wir ein anderes Beispiel: L = 2,5λ, darn ist d = 2 λ and Θ = cos-1((2,5 - 0,5) / 2,5), Θ = 36,9°, zu sehen auf Bild 3.
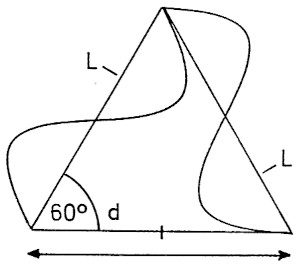
Bild 2: Zwei Schenkel einer 1-λ-Rhombusantenne. Die Strecke d ist um 0,5 λ kürzer als ein Schenkel. Die raumliche Phase zwischen beiden Schenkeln ist 0,5 λ.
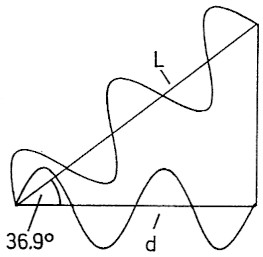
Bild 3: Erklarung der Phasenmethode: Die Schenkelkinge ist urn 0,5 λ longer als die Strecke d in Senderichtung.
2. Eine Naherungslösung fur maximales Θ
Wir gehen wieder auf Gleichung [1] zuruck, wir differenzieren und setzen den Differentialquotient gleich null. Nach einigen Umrechnungen bekommen wir:
πL (sin2 Θ) = tan (πL (1 - cos Θ)) [3]
Um die linke Seite in eine geschmeidige Form zu bringen, benutzen wir nach dem Satz des Pythagoras den folgenden Ausdruck:
sin2 Θ = 1 - cos2 Θ = (1 + cos Θ)(1 - cos Θ)
Dann erhalten wir:
πL (1 + cos Θ)(1 - cos Θ) = tan πL(1- cos Θ))
Bei recht langen Drahten (> 3 λ) ist der Winkel Θ nicht allzu groß und wir konnen als Naherung (Approximation) annehmen:
(1 + cos Θ) = 2. So wird daraus:
2πL (1 - cos Θ) = tan (πL (1 - cos Θ))
Jetzt vereinfachen wir noch L (1 - cos 0) = K, und erhalten darn nach (2):
2πK = tan (πK)
Der letzte Ausdruck ist eine goniometrische Gleichung mit zahlreichen Lösungen für K. Wir verwenden n als Nummer der Strahlungskeule und K als dazugehorige Konstante. Die sich ergebenden Werte sind in der folgenden Tabelle dargestellt:
| n | K |
|---|---|
| 1 | 0,371 |
| 2 | 1,466 |
| 3 | 2,480 |
| 4 | 3,485 |
| 5 | 4,489 |
| 6 | 5,491 |
| 7 | 6,492 |
| 8 | 7,493 |
| 9 | 8,494 |
| 10 | 9,495 |
| 11 | 10,495 |
Für höhere als die elfte Strahlungskeule ist ungefahr: K = n -0,5. K wird wie folgt abgeleitet:
πL(1 - cos Θ) = K × π
1 - COS Θ = K/L
cos Θ = 1 - K/L
Θ = cos-1 (1 - K/L) [4]
Als praktisches Beispiel nehmen wir wieder eine Langdrahtantenne der Lange L = 2λ. Aus [4] mit n = 2 and K = 0,371 erhalten wir für das Maximum der ersten Strahlungskeule:
Θ = cos-1 (1 - 0,371 / 2)Θ = cos-1 (0,8145)
Θ = 35,5°
Für das Maximum der zweiten Strahlungskeule bekommen wir von [4] mit n = 2 und K = 1,466 aus der Tafel:
Θ = cos-1 (1 - 1,466 / 2 )
Θ = cos-1 (0,267)
Θ = 74,5°
Eine dritte Strahlungskeule existiert nicht. Dies deutet sich dadurch an, class der Wert in der Klammer negativ wird. Die Ergebnisse dieser Rechnungen sired auf Bild 4 zu ersehen.
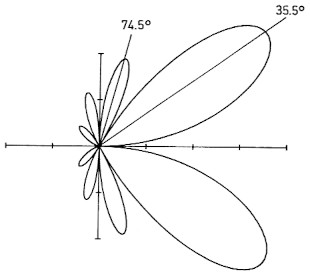
Bild 4: Näherungsmethode: Die errechneten Winkel der Maxima sind nur urnvesentlich grolier als die der tatsochlichen Maxima.
3. Die Lüsung für maximales 0 durch Probieren
Wir kehren zu der exakten Formel [3] zurück:
πL (sin2 Θ) = tan (πL (1 - cos Θ))
Als Beispiel wahlen wir wieder einen Langdraht mit L = 2 λ und dem durch Naherung gefundenen Winkel von 35,5°. Der wissenschaftliche Taschenrechner berechnet beide Seiten der Gleichung:
| Θ | linke Seite | - | rechte Seite | = | Differenz |
|---|---|---|---|---|---|
| (sin2 Θ) | - | tan (2π(1-cos Θ)) | = | D | |
| 35,5° | 2,1188 | - | 2,3466 | = | -0,2278 |
| 36° | 2,1708 | - | 2,5720 | = | -0,4012 |
| 35° | 2,0671 | - | 2,1548 | = | -0,0877 |
| 34,5° | 2,0157 | - | 1,9895 | = | +0,0262 |
Je geringer die Differenz, umso genauer die Losung. Wir sehen, dass der gesuchte Winkel des Strahlungsmaximums zwischen 35° und 34,5° liegt. Wir wagen einen letzten Versuch:
34,6° 2,0260 - 2,0208 = +0,0052
Mit dieser zeitraubenden Prozedur konnen wir den Winkel des Maximums in jeder gewünschten Genauigkeit ermitteln. Genauigkeiten besser als 0,5° ergeben aber in der Praxis keinen Sinn.
4. Lüsung für den Winkel des Strahlungsmaximums durch numerische Mathematik
Leicht zu verstehen und auch zu berechnen ist es, die Gleichung [1] mit einem Computer zu lösen und anzuhalten, wenn FΘ gerade sein Maximum überschritten hat. Die nachste Tafel zeigt ein gates Beispiel. Wir nehmen wiederum L = 2 λ und Winkelschritte von 0,1°. Der Computer berechnet die Werte von FΘ aus [1]:
| L | Θ | FΘ |
|---|---|---|
| 2 | 34,4° | 2,877.331 |
| 2 | 34,5° | 2,877.494 |
| 2 | 34,6° | 2,877.564 (Maximum!) |
| 2 | 34,7° | 2,877.540 |
Das Maximum für die erste Strahlungskeule liegt bei 34,6°. Jetzt suchen wir das Maximum der zweiten Keule. Wir fangen ein Grad vor Θ = 74,5° an, die wir aus Formel [4] berechnet haben:
| L | Θ | FΘ |
|---|---|---|
| 2 | 73,5° | 1,308.693 |
| 2 | 73,6° | 1,309.224 |
| 2 | 73,7° | 1,309.606 |
| 2 | 73,8° | 1,309.840 |
| 2 | 73,9° | 1,309.926 (Maximum!) |
| 2 | 74,0° | 1,309.865 |
Das Programm daze in BASICA ist im Anhang ausgedruckt. Zusammenfassend haben wir drei Methoden kennen gelernt, die Winkel der Strahlungsmaxima zu ermitteln: Die Phasenmethode, die Nuherungsmethode und als befriedigendste Losung die Berechnung mit der numerischen Mathematik. Bild 5 demonstriert uns die drei Losungen im Vergleich. "Phase" enthalt die grol3te Abweichung "Approx (Naherung)" ist nur bei kurzen Langen beachtlich ungenau und "Real" ist ideal; doch aufwendig zu rechnen.
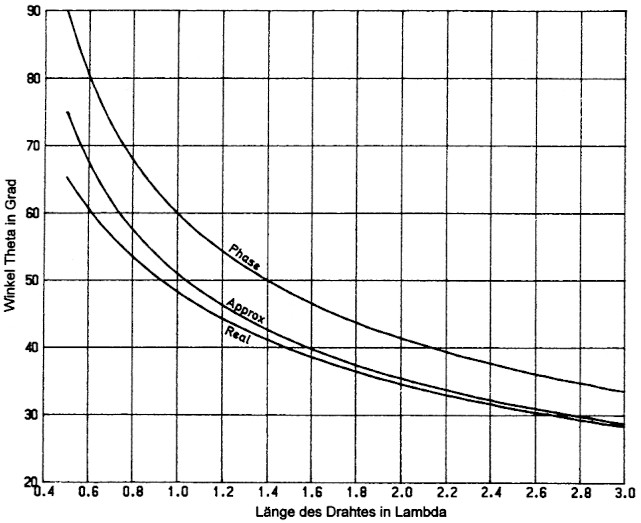
Bild 5: Phasenmethode, Approximationsmethode und tatsüchlicher Winkel der Strahlungsmaxima im Vergleich.
Langdrahte in Stehwellen erregt
Verhaltnismal3ig kurze Drahte, etwa von 1 λ bis 3 λ lassen sich meist nur in Stehwellen erregen, auBer es werden besondere MaBnahmen zur Wanderwellenerregung getroffen. Der Polarkoefüzient oder Formfaktor für die Stehwellenerregung ist bekanntlich:
FΘ = ((cos(πL × cos Θ) - cos πL) + j(sin(πL × cos Θ) - sin (πL) × cos Θ)) / sin Θ [5]
L ist die Lange in λ,
j = der imaginare Operator
Uberraschende Ergebnisse ük die Strahlungsmaxima mit Stehwellenerregung
Für die Konstruktion von V- und Rhombusantennen ist die genaue Richtung der Hauptkeule von entscheidender Bedeutung. Wir massen also das erste Maximum und seine genaue Richtung suchen. Als Grundlage dient üns dazu die Formel [5]. Ein Computerprogramm berechnet daraus den Formfaktor, stellt ihn auf dem Bildschirm in Zahlen dar und halt an, sobald das Maximum überscluitten ist und der Formfaktor wieder kleiner wird. Dieses Programm ist in BASICA im Anhang abgedruckt. Auf diese Weise erhalten wir nach zahireichen Rechnungen das Diagramm von Bild 6. Urn nichts zu übersehen, ha-ben wir die Rechnung feinstuüg vorgenommen und haben die Lange des Drahtes in kleinen Schrittchen von nur 0,05 λ. gesteigert. Damit sich keine Irrtümer einschleichen, wurden die Winkel mit einer Genauigkeit von +/- 0,05 Grad berechnet. Die Kurve der optimalen Winkel ist deutlich in zahlreiche Maxima und Minima gegliedert. Die Maxima stellen sich ein bei Drahtlangen von L = 1; 1,5; 2; 2,5 and 3 λ. Das ist gerade dann, wenn die Strahlungscharakteristiken dieser Antennen Nullwinkel haben.
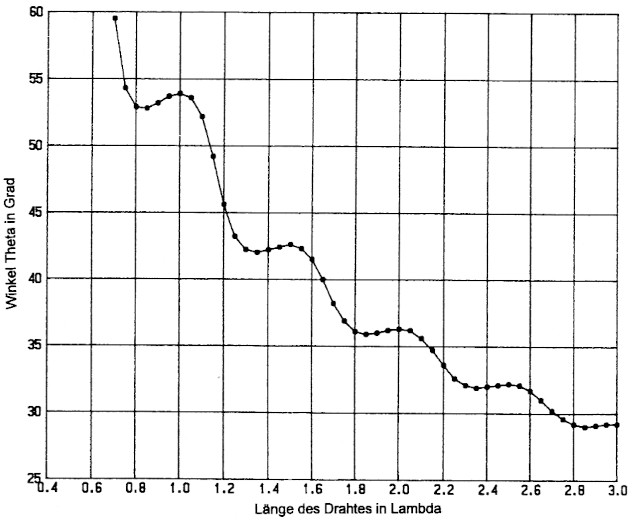
Bild 6: In Stehwellen erregte Langdrahtantenne. Der Winkel des Strahlungsmaximums der ersten Keule. Deutliche Oszillationen!
Bis zu dieser Veroffentlichung und bis zum heutigen Tag wurde allgemein angenommen, die hier dargestellte Kurve würde ruhig und ausgeglichen verlaufen. Sie ist aber gegliedert in Maxima, Minima und Wendepunkte. Die bisherige, einfache Regel "Je langer der Draht, umso kleiner der Winkel" hat keine Gültigkeit mehr.
Die auffallige Struktur der Kurve konnte kein Zufallsergebnis sein. Aber es war noch eine Bestatigung der neuen Tatsache notwendig. Als Prüfstein wurde die zweite Keule des Strahlungsdiagramms gewahlt und wiederum die Lange des Drahtes in kleinen Schritten von 0,05 λ gesteigert. Die zweite Keule tritt erstmals bei L = 1,25 λ auf und strahlt bis L = 1,7 λ im Winkel von 0 = 90°. Erst dann beginnt ihr Winkel abzufallen und bildet in Bild 7 die auffallige Wellenlinie. Durch den flachen Verlauf gibt es keine Maxima und Minima mehr; aber die Kurve wird nun durch Wendepunkte bei 2 λ, 2,5 λ und 3 λ gegliedert. Durch die Struktur der Winkel auch der zweiten Keule ist der Beweis erbracht, dass die Struktur nicht zufallig entstanden ist.
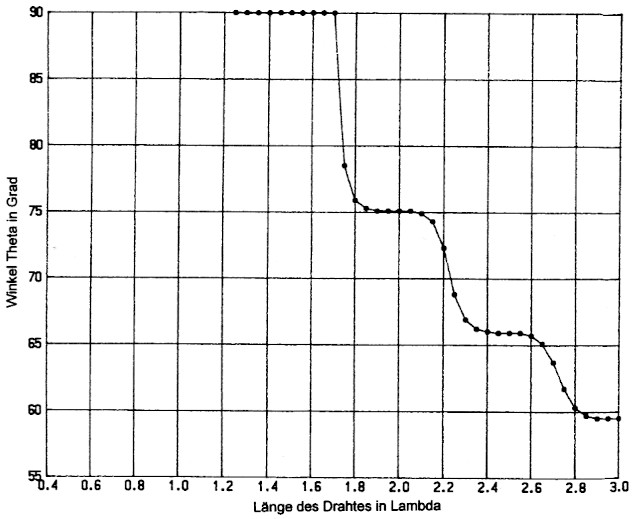
Bild 7: In Stehwellen erregte Langdrahtantenne. Der Winkel des Strahlungsmaximums der zweiten Keule. Oszillationen!
Praktische Konsequenzen fur verbesserte V-Antennen
Die V-Antenne, die Rhombusantenne und die Rhomboidantenne sind von den Winkeln der maximalen Strahlung ihrer Drahte abhangig. So liegt es sehr nahe, zu untersuchen, ob die soeben entdeckte Struktur der Winkelkennlinie einen Einfluss auf die Abstrahlung dieser Antennen hat. Da Rhomben und Rhomboide nicht allzu hauüg vorkommen, wurde die Untersuchung auf eine V-Antenne der Schenkellange 0,5 λ bis 3 λ bescltrankt. Mit EZNEC 2000 (1) ünden wir erstaunliche Ergebnisse. Die V-Antenne besteht aus einem sehr kleinen Mittelstück zu Speisezwecken der Lange 0,02 λ (11 Segmente) und zwei langen Schenkeln zur Abstrahlung (jeder 110 Segmente). Alle Drahte haben 3 nun Durchmesser und bestehen aus Kupfer. Die Grundfrequenz ist 14 MHz.
Zuerst wird die Schenkellange festgelegt und dann der Winkel zwischen den Drahten verandert, so lange, bis das Maximum an Feldstarke erreicht ist. Die Anderung des Spreizwinkels geschieht durch Ortsveranderung der beiden AuBenmasten. Dadurch werden deren Koordinaten X und Y verandert. Nur um es festzulegen, wird ürdie Schenkel eine Bauhohe von λ/2 angenommen; aber alle Rechnungen beziehen sich auf den Freiraum. Der Winkel 0 ist der selbe wie bei alien vorhergehenden Rechnungen mit dem Einzeldraht. Das heiBt: Der Spreizwinkel zwischen den V-Schenkeln ist doppelt so groB. Die ersten Ergebnisse stellen sich wie folgt dar:
L Θ g
0,5 λ 86° 3,93 dBi
0,55 λ 85° 4,51 dBi
0,6 λ 83° 5,09 dBi
L = Lange eines Schenkels,
Θ = optimaler Halbwinkel zwischen den Schenkeln,
g = optimaler Gewinn
Unter diesen Voraussetzungen wurden die Rechnungen in Schritten von 0,05 λ bis zu L = 3 λ durchgeführt. Der kleinste Winkelschritt war 0,5°. Die optimalen halben Spreizwinkel sind in Bild 8 dargestellt. Die Gliederung der Kurve ist offensichtlich, aber nicht mehr so ausgepragt wie bei den Einzeldrahten. Dies ist eine Folge der gegenseitigen Verkopplung der Felder am den einzelnen Schenkeln. Der Knick bei 1,1 λ ist auffallig. Dieser bemerkenswerte Punkt ist zuerst von Thiele and Ekelman(3) gefunden worden. Sie berechneten die V-Antenne in groBen Schritten von λ/4 und konnten so keine Kurve zeichnen; aber ihre Ergebnisse fallen mit den hier gezeigten Resultaten zusammen.
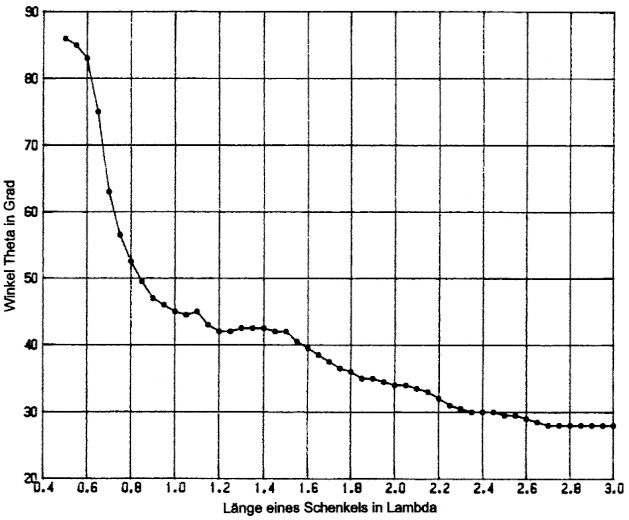
Bild 8: Der optimale Halbwinkel zwischen den Schenkeln einer V-Antenne in Abhüngigkeit von der Schenkelkinge, berechnet mit EZNEC.
Die wellenformige Struktur der Kurve ist besonders auffallig bei der Darstellung des optimalen Gewinnes einer V-Antenne in Bild 9. Ganz frappierend ist die Formation der Gewinnumkehr bei L = 1 λ. Die Gewinnumkehr bedeutet, dass eine V-Antenne mit Schenkeln von 0,85 λ mehr Gewinn erbringt als eine V-Antenne mit langeren Schenkeln von 1,05 λ. Mit dem Anwachsen der Schenkellange über 1,1 λ hinaus zeigt der Gewinn noch ein sehr deutliches Auf and Ab; hat jedoch keine Gewinnumkehr meter. Diese Formation ist so auBergewohnlich, dass wir mit EZNEC die Elevations- und Azimutaldiagramme der 0,85-λ-V-Antenne dargestellt haben, um naher an die Ursachen zu kommen.
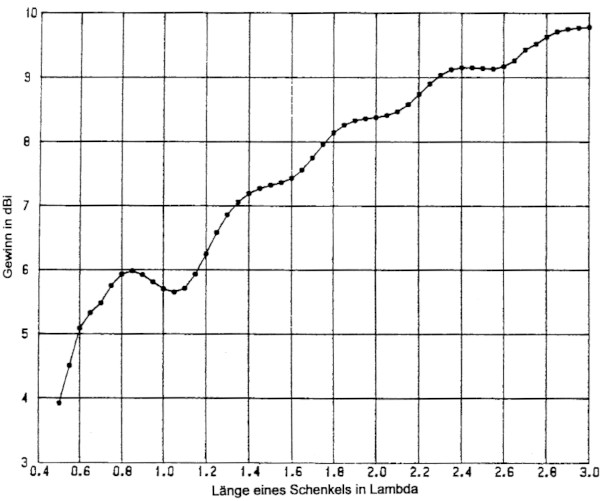
Bild 9: Freiraumgewinn einer V-Antenne, berechnet mit EZNEC. Auffällig und neu: die Umkehrformation zwischen 0,85 λ, und 1,05 λ.
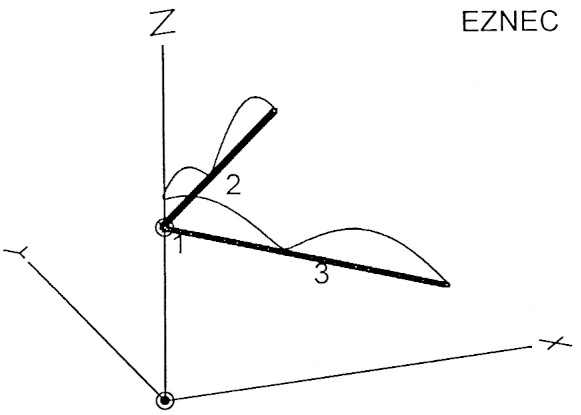
Bild 10: Die optimierte 0,854-λ-V-Antenne.
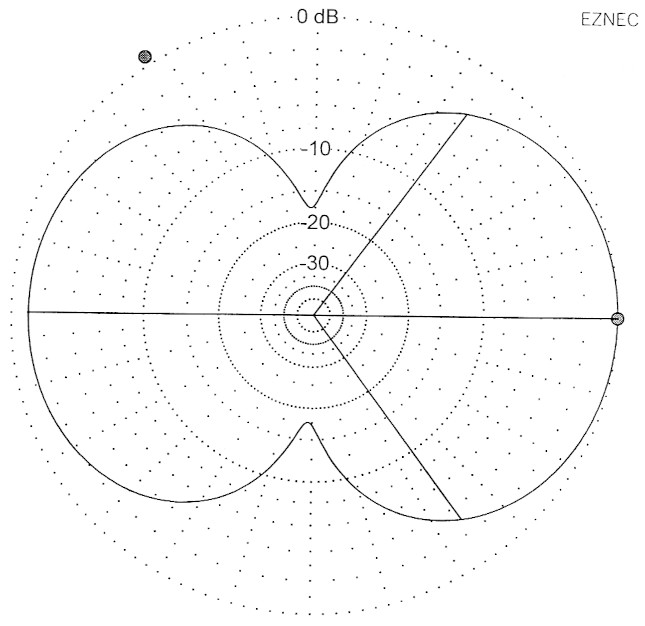
Bild 11: Elevations- oder Vertikaldiagramm der 0,85-λ-V-Antenne, breit und behabig.
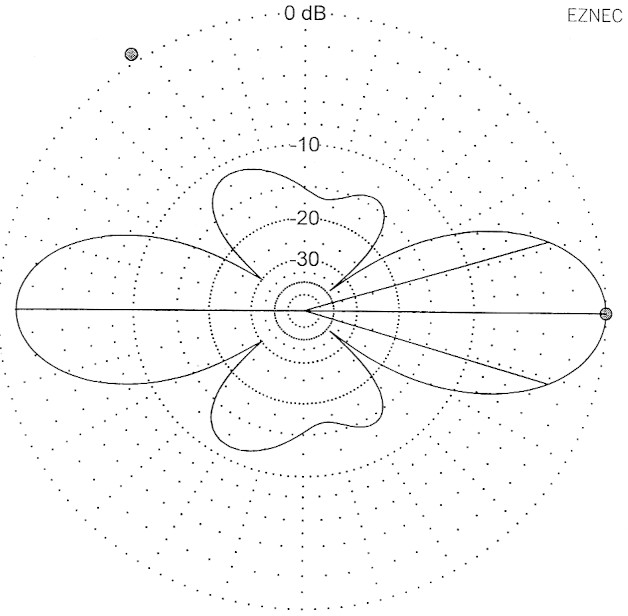
Bild 12: Azimutal- oder Horizontaldiagramm der 0,85-λ-V-Antenne, gut gebündelt mit geringen Nebenkeulen.

Quellen und Literatur
- ENE 2000, Roy Lewallen, W7EL, P. O. Box 6658, Beaverton, OR 97007, USA
- Laport and Veldhuis, Improved antennas of the rhombic class. RCA Review 21(1960) Vol. 3, p. 117-123
- Thiele and Ekelman, Design formulas for vee dipoles. IEEE Transaction on antennas and propagation. Vol. AP-28, No 4. July 1980
DL1VU, Karl H. Hille.