Resonanz oder Reflexion? - Was in Leitungs- und Topfkreisen passiert
Bei Frequenzen Ober etwa 100 MHz benum man manchmal vorteilhaft Kabelstlicke staff eines Schwingkreises mit diskreten Bauelementen, im UHFBereich sind solche Schwingkreise iiberhaupt nicht mehr einsetzbar, und man greift zum Topfkreis.
Zumindest im Amateurbereich scheint die Meinung vorzuherrschen, dass Leitungskreis (Kabelstack) und Topfkreis (stares Gebilde) elektrische Aquivalente zum konventionellen Schwingkreis mit diskretem Kondensator und diskreter Spule sind. Die jeweils verwendete Bezeichnung "...kreis" deutet ja darauf hin. Das andert aber nichts an der Tatsache, dass diese Gebilde grundsatzlich anders funktionieren als ein diskreter Schwingkreis.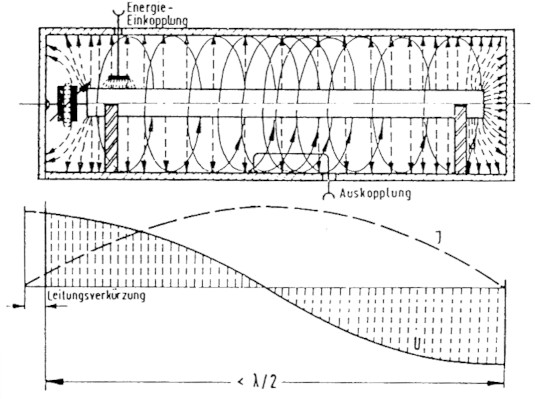
Was ist Resonanz?
Resonanz bedeutet allgemein u. a. Mitschwingen. Hierbei entsteht ein extremer Schwingzustand.
Ein Schwingkreis ist in Resonanz, wenn bei konstanter Einkopplung die Spannung an Kondensator und Spule maximal ist. Das gilt ftir Parallel- und Serienkreis! Beim Serienkreis mag das den Praktiker etwas verwundern, weil ja die Spannung fiber beiden Bauelementen im Resonanzfall minimal ist. Dies trifft aber nicht auf L oder C allein zu! Es sind also stets Bauelemente mit einer gewissen Spannungsfestigkeit erforderlich.
Bei Resonanz kompensieren sich die Blindwiderstande von diskretem Kondensator (negativer Blindwiderstand) und diskreter Spule (positiver Blindwiderstand). Dies ist die einzige Voraussetzung fair Resonanz, sozusagen ihr "Markenzeichen".
Wie Koch die Spannung an Kondensator und Spule wird, hangt allein von der Betriebsgiite ab. Also nicht nur von den Verlusten der Schwingkreis-Bauelemente, sondem auch von Quellwiderstand, Lastwiderstand und Grad der Kopplung von Quelle und Last. Die Physik lasst sich auch hier nicht iiberlisten: Wird beispielsweise die Spule eines Parallelkreises bei 1/10 angezapft und dort eine Quelle angeschlossen, dann ist die Spannung am Hochpunkt zwar exakt zehnmal groBer als die an der Anzapfung, diese Spannung ist aber stets geringer als die Leerlaufspannung des Generators.
Und wir wissen: Kennt man (diskrete) Kapazitat und Induktivitat, kann man die Resonanzfrequenz berechnen. Ein Parallel- oder Serienkreis mit 77 pF und 3,3 µH beispielsweise ist auf 10 MHz resonant.
Zeigen Leitungen Resonanz?
Auch an einem Kabel kann man eine Kapazitat und eine Induktivitat messen. Ein 1 m langes Stuck Ecoflex 15 zum Beispiel bietet uns 77 pF, wenn es offen ist. Dann lasst sich natiirlich keine Induktivitat messen. Das gelingt nur, wenn es am Ende kurzgeschlossen ist. Ich habe die Induktivitat nicht gemessen; sie muss aber deutlich größer sein als die eines 2 m langen gestreckten Leiters, der etwa 2 µH aufweisen wiirde, also nehmen wir mal 3,3 µH an. In diesem kurzgeschlossenen Zustand aber kann man wiederum keine Kapazitat messen.
Die Tatsache "entweder C (offen) oder L (kurzgeschlossen)" lasst uns schon sehr skeptisch werden bei dem Versuch, ein Kabel mit einem Schwingkreis zu vergleichen. Daher erstaunt es uns auch nicht sehr, dass dieses Stuck Leitung, egal ob offen oder kurzgeschlossen, bei ungefahr 10 MHz kein auffallend abweichendes Impedanzverhalten zeigt. Wenn wir die Frequenz (beispielsweise eines angekoppelten KW/VHF-Dippers) langsam erhohen, dam zeigen sich erst bei 64,5 MHz und dann nochmals bei 193,5 MHz Extremwerte der Eingangsimpedanz. Ist das Kabel kurzgeschlossen, benimmt es sich bei diesen Frequenzen, die sich um den Faktor 3 unterscheiden, fast wie ein Isolator, ist es offen, wirkt es fast wie ein Kurzschluss. Konnten wir die Frequenz noch weiter erhohen, warden wir eine Wiederholung des Verhaltens bei nochmaliger Frequenzverdreifachung feststellen usw.
Dieses Benehmen lasst sich leicht erklaren, wenn man weiß, was auf Leitungen geschieht. Im Gegensatz zu einem Schwingkreis kommt es hier zur Ausbildung einer elektromagnetischen Welle, welche die Leitung entlang lauft und am Ende vollstandig reflektiert wird. Bei einem Verkarztmgsfalctor von 0,86 ist unser Kabel elektrisch rued 1,16 m lang und stellt für die Wellenlange 4,65 m entsprechend der Frequenz 64,5 MHz ein Viertelwellenstack dar. Dieses zeigt genau das beschriebene Verhalten aufgrund der am Kabeleingang auftretenden Phasenbeziehung zwischen angelegter Spannung (hineinfließendem Strom) und Spannung (Strom) der dort ankommenden reflektierten Welle.
Auch das bei Frequenzverdreifachung immer wiederkehrende Verhalten ist schnell erklart. Wird die Frequenz verdreifacht, wird dem Gebilde gewissermaBen ein Halbwellenstack hinzugeftigt. Dieses transformiert grundsatzlich 1:1, man kann es sich also wegdenken. Ubrig bleibt wieder ein Viertelwellenstack (Bild 1).
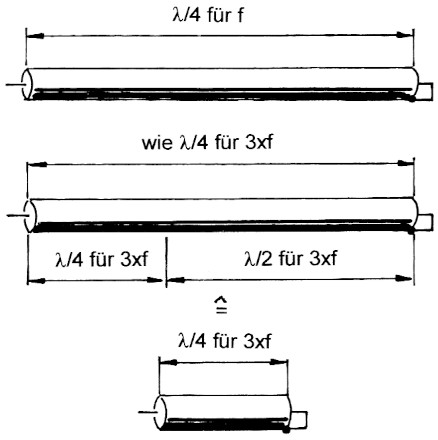
Bild 1: 1st ein Kabel bei der Frequenz f elektrisch 1/4 Wellenkinge long, so zeigt es bei der Frequenz 3xf das gleiche Verhalten.
Bild 2 beweist eindrucksvoll den Unterschied im elektrischen Verhalten zwischen Schwingkreis und Kabel. Dinge, die sich grundsatzlich so verschieden verhalten, milssen sich such in Aufbau and Funktion grundsatzlich unterscheiden. Ein Leitungskreis verdient seinen Namen nicht, denn er ist kein Schwingkreis. Sein Verhalten ahnelt dem eines echten Schwingkreises nur nahe der "Resonanzfrequene - ein ebenfalls unpassender Begriff, denn hier kommt es nicht zu einem Mitschwingen, einer Erregung, einem extremen Schwingzustand. Extrem sind hier Reflexion (Totalreflexion) and Phasenbeziehung zwischen den sich am Kabelanfang treffenden GroBen (0° bzw. 180°).
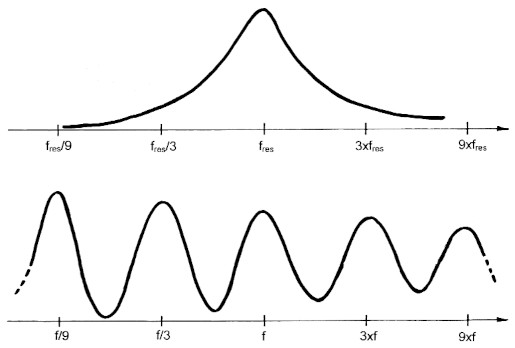
Bild 2: Impedanz eines Parallelschwingkreises (oben) und einer Leitung über der Frequenz. Die Verengung nach rechts wird durch die steigende Damp fung hervorgerufen.
Resonator - verdient er seinen Namen?
Man unterscheidet mechanische and elektrische Resonatoren. Mechanische Resonatoren konnen durchaus "etwas Elektrisches an sich haben", namlich durch elektrischen Strom erregt werden. Ein solcher Resonator ist beispielsweise ein piezoelektrischer Festkorper (Quarz), der mit Elektroden versehen wurde. Auch Keramikfilter und mechanische Filter sind mechanische Resonatoren. Immer basiert die Funktion auf einem extremen Schwingzustand. Der Begriff "Resonanz" kommt ja aus der Mechanik (Physik, Musik). Hier also eine richtige Bezeichnung.
Ein elektrischer sogenannter Resonator funktioniert jedoch im Prinzip wie ein Stuck Kabel. Die Bezeichnung "Resonator" ist also ebenso unangebracht wie die Bezeichnung "Kreis", und dennoch sind diese Gebilde hauptsachlich unter dem Begriff "Topfkreis" bekannt.
Topfkreise benutzt man besonders im UHF-Bereich und hoher, denn hier konnen Kondensator-Zuleitungsinduktivitat und Spulen-Parasitarkapazitat nicht mehr vemachlassigt werden. Ein wirklich diskreter Schwingkreis lasst sich nicht mehr aufbauen. Ein Topfkreis zeichnet sich folglich durch eine "Hauptresonanz" und mindestens eine "Nebenresonanz" aus.
Vorteilhaft baut man diese Gebilde mit kompakt aus Blechen zusammengeloteten oder aus Vollmaterial gedrehten Gehausen, die einen zentralen Leiter besitzen, also im Prinzip eine unsymmetrische Leitung darstellen. Folglich kommt es auch hier zur Ausbildung einer elektromagnetischen Welle, welthe reflektiert wird, da das Gebilde entweder kapazitiv abgeschlossen oder- seltener - vollig kurzgeschlossen betrieben wird. Im Gegensatz zu einem Snick Leitung kann die elektrische Lange hier eingestellt werden. Dazu dient im ersten Fall ein integrierter Trimmer kleiner Kapazitat and hoher Gine, der die Leitung elektrisch verkiirzt und im zweiten Fall ein Kurzschlussschieber, der die Leitung mechanisch und somit auch elektrisch verkiirzt.
Man unterscheidet in der Ausfiihrung zwischen Wendeltopfkreis, den man auch Helicalkreis oder -resonator nennt, und Koaxialtopfkreis, den man auch Koaxialresonator nennen kann. Der Unterschied liegt in der Gestalt des Innenleiters: wendelformig oder gestreckt. Es ist anzumerken, dass der Wendeltopfkreis keinen homogenen Aufbau besitzt, also eine deutliche Abweichung vom Ideal einer HF-Leitung aufweist. An jedem Punkt der Leitung ist jedoch der Abstand zwischen Innenleiter und Aul3enleiter gleich.
Weitere theoretische und praktische Informationen bringt(1).
Frank Sichla, DL7VFS.