Neues von den Groundplane-Antennen
In der Antennentechnik geht eine Antenne aus der anderen hervor. Wir brauchen nur einen logischen Schritt welter zu schreiten, um aus einer Antenne eine neue zu entwickeln: Zeppelin-Antenne, Fuchsantenne, Doppelzepp, Extended Double Zepp. Die Ietzten drei Antennen sind alle besonders gestaltete Dipole. Schneiden wir sie in der Mitte auseinander, so entsteht daraus eine umfangreiche neue Klasse: die Monopole. Damit diese liberhaupt wieder funktionieren, mussen die Entwickler der Monopole bestrebt sein, die den armen Wesen weggeschnittene Halite wieder zu ersetzen. Sie suchen sich als "bessere Halite" die Erde aus, die wir mal sehr wohlwollend als gut leitend ansehen wollen.
Entstehung der Groundplane
In Wirklichkeit ist die Erde alles andere als ein guter elektrischer Leiter, der Ausdruck Halbleiter ist besser angebracht. Urn nun dieser ungeliebten Erde zu entkommen, haben sich die Antennenphysiker etwas Besonderes ausgedacht: die Groundplane. Dieses Gebilde soil die Erde ersetzen oder genauer ausgedrackt: Die Groundplane ersetzt die fehlende Antennenhalfte, die man dem Dipol vorher genommen hat. Deswegen nennt man sie auch aus gutem Grand Gegengewicht. Da es nichts absolut Neues gibt, muss man für die Groundplane auch die Formen des Dipols wahlen, wobei man natarlich große Freiheit in der Gestaltung der Form hat. Gehen wir vom Halbwellen-Dipol aus, so ist die vorhandene Halfte ein Leiter mit der Lange einer Viertelwelle. Die andere, die Erde ersetzende Halite muss genau so lang sein, um die Symmetric zu wahren. Also ist die Groundplane ebenfalls elektrisch eine Viertelwelle lang. Bei einer vertikalen Halbwellenantenne ware der zu ersetzende Teil erst mal senkrecht und eine Viertelwelle lang. Das ist meistens zu viel und nur durch eine gewaltige Höhe der Antenne zu bewaltigen. Also gehen wir ab von der vertikalen Lage und knicken die Groundplane waagerecht ab (Bild 1). Damit haben wir die Urform der Groundplane geschaffen: ein horizontaler Viertelwellendraht.
Bild 1: So wird aus dem Vertikaldipol eine "einbeinige" Groundplane-Antenne.
Verminderung der Verluste
Natilrlich ist these Urform alles andere als vollkommen, vor allem fehlt die notwendige Symmetric. Die konnen wir ganz leicht herstellen, wenn wir einen zweiten Viertelwellendraht in die entgegengesetzte Richtung spannen. Damit steht der senkrechte Strahler auf einer waagerechten Halbwelle als Groundplane (Bild 2). Hurra, die Symmetric ist gewahrt! Diese Anordnung hat noch den Vorteil, dass sich der Strom in zwei Leiter verzweigt. Dies vermindert die Verluste: Bei einer einbeinigen Groundplane ist die verlorene, ohmische Leistung P = I2 × R. Bei der zweibeinigen Ground-plane ist der Verlust in einem Zweig P = ½2 × R. In beiden Zweigen ist die Verlustsumme Pges = 2 × ½2 × R. Das ergibt ausgerechnet: Pges = 2 × ¼ × P × R = ½ × F × R = 0,5 × I2 × R. Die Verlustsumme ist immerhin auf die Halite zusammengeschrumpft, und dies durch eine ganz einfache Maßnahme. Wenn wir diese Rechnung fortsetzen und als Strom in der Groundplane 1 Ampere sowie einen Verlustwiderstand von 1 Ω im Leiter annehmen, erhalten wir die erfreulichen Werte in Tabelle 1.
| Zahl der Leiter | Strom je Leiter | Verlust je Leiter | Gesamtverlust |
|---|---|---|---|
| 1 | 1,00 λ | 1,0000 W | 1,00 W |
| 2 | 0,50 λ | 0,2500 W | 0,50 W |
| 3 | 0,33 λ | 0,1100 W | 0,33 W |
| 4 | 0,25 λ | 0,0625 W | 0,25 W |
| 5 | 0,20 λ | 0,0400 W | 0,20 W |
Bei zehn Zweigen der Groundplane hatten wir nur noch ein Zehntel des urspriinglichen Verlustes, bei 100 Leitern waren es nur noch 1/100 oder 1 %. Leider wachsen die Baume nicht in den Himmel: Die Leiter der Ground-plane sind mit der verlustreichen Erde gekoppelt, und dies verschlechtert das gute Ergebnis.
Die zweibeinige Groundplane von Bild 2 ist zwar klappsymmetrisch aber nicht drehsymmetrisch. Erst bei Drehsymmetrie strahlt die Monopolantenne gleich stark in alle Himmelsrichtungen. Fügen wir einen weiteren Zweig hinzu, dann kommen wir zu der dreibeinigen Groundplane von Bild 3. Weil die drei Leiter drei Füße bilden, wird solch eine GroundplaneAntenne auch Triple-Leg-Antenne genannt. Diese Antenne wurde von Ted, HB9OP, entwickelt. Angeblich strahlt sie besonders stark und sehr flach in der Winkelhalbierenden der Leiter, was Professor Dr. Janzen, in seinem ausgezeichneten Buch(3) allerdings nicht bestätigt. Sie strahlt vielmehr vollkommen rund im Azimut und ist daher bereits ein perfekter Rund-strahler, der z. B. für Rundfunkzwecke eingesetzt werden kann. Die Leiter der Groundplane sind immer gleich lang und gehen vom Mittelpunkt eines Kreises aus, so dass ihre Endpunkte den Umfang eines Kreises bilden. Sehr zu recht konnen wir diese Leiter als Radien dieses Kreises betrachten und sie deswegen Radials nennen, ein Ausdruck, der sich weltweit eingeburgert hat.
Bild 2: Klappsymmetrische, zweibeinige Groundplane-Antenne.
Bild 3: Drehsymmetrische, dreibeinige "TripleLeg-Antenne".
Radials reflektieren nicht
Die Groundplane aus Radials hat bei alien Vorziigen nur einen Nachteil: Sie reflektiert die Wellenzuge, die vom Straitler ausgehen, leider nicht. Die Strahlung der Antenne geht nahezu unbeeinflusst durch die Radiale hindurch und seien es noch so viele. Deswegen ist der Einfluss der Erde durch die Groundplane nicht zu verhindern. Erst ein Erdnetz aus engem Maschendraht konnte reflektieren, dazu ist es aber meistens viel zu klein. Die Groundplane erftillt dagegen eine andere Eigenschaft sehr getreu: Sie sorgt ftir eine niedrige Impedanz, an der sich der Mantel des speisenden Koaxialkabels richtig "wohl fühlt". Die HF-Spannung ist sehr gering, und bei geschickter Auslegung treten nicht einmal Mantelwellen auf. Für die Speisung hat also die Groundplane sehr große Bedeutung, fiir die Reflexion kann ihre Wirkung vernachlassigt werden. Dagegen ist der Einfluss der reflektierenden Erde auf eine Groundplane-Antenne sehr betrachtlich und wirkt sich auf den Gewinn und auch auf die Strahlungscharakteristik aus, wie wir spater noch sehen werden.
Die Groundplane-Antennen und EZNEC
Das bereits erwahnte Buch Ober Monopol- und Vertikalantennen von Prof. G. Janzen(3) befasst sich ausführlich und tiefgriindig mit Groundplane-Antennen. Es wurde noch mit EZNEC 2.0 erstellt, was den interessanten Resultaten wirklich nicht zum Nachteil gereicht. Wichtig ist die in EZNEC enthaltene Methode der Segmentierung von Antenne und Radial.
Unter Segmentierung verstehen wir die Aufteilung des strahlenden Leiters in kleine und sehr ldeine Abschnitte, um die Antenne iiberhaupt berechnen zu konnen. Jedes Segment (Abschnitt) fiihrt einen Strom, der strahlt, und es tibt auf jedes andere Segment einen Einfluss aus. Wenn wir 20 Segmente haben, ergeben sich 20 ×20 = 400 gegenseitige Einflüsse durch die Kopplung aufeinander. Das ist eine Riesenmenge an Rechnungen, die für einen Computer das gefundene Fressen sind; denn der wird rasch damit fertig. Die gauze Rechenart von Segment auf Segment nennen wir Momentenmethode, und die gehort zur schwarzen Mathematik(1),(2). Ob das nun mit EZNEC 2.0 oder mit EZNEC 2000 gerechnet wird, ist unwesentlich, die Ergebnisse sind die gleichen.
Gewinnwarnung
Eine Gewinnwarnung wird von einer Aktiengesellschaft ausgesprochen, wenn der Gewinn nicht so gut ausfallt, wie man sich dies erhofft hatte. In Folge davon purzelt der Aktienkurs betrachtlich nach unten. Hier ist es nicht ganz so schlimm: Die EZNEC-Gewinnzahlen sollen berechtigter Kritik unterzogen werden. Wie ich feststellen musste, sind die von EZNEC 2000 berechneten Gewirmzahlen nicht stabil, sondern sie hangen stark von der Anzahl der Segmente ab.
Dazu ein einfaches Beispiel: Eine Groundplane-Antenne hat vier Radials von je 5,4 m Lange und einen vertikalen Strahler von 5,4 m höhe. Alle Leiter bestehen aus 2 mm Kupferdraht. Die horizontale Groundplane liegt 2 m Koch fiber normaler Gartenerde. Rechnet EZNEC mit einem Segment je Leiter, so hat diese Antenne bei 14 MHz einen Gewinn von 3,58 dBi. Bei drei Segmenten je Leiter geht der Gewinn schon auf 2,63 dBi zunick und bei neun Segmenten sind es 1,49 dBi. Bei 99 Segmenten ist der Gewinn auf -0,45 dBi zusammengeschrumpft. Einen Begriff von dem Gewinnabfall, wie der mit der Anzahl der Segmente fortschreitet, bietet Bild 4. Lassen wir diese Groundplane-Antenne im freien Raum strahlen, so geht der Gewinn, der bei einem Segment 4,85 dBi betragt, ebenfalls zunick. Bei 99 Segmenten sind es nur noch 1,34 dBi! Die verlustreiche Erde ist also an dem Gewinnabfall nicht schuld. Bei einem Halbwellendipol im Freiraum, der eigentlich 2,15 dBi Gewinn ha-ben miisste, ist es nicht so schlimm: Ftinf Segmente: 2,01 dBi, 499 Segmente: 2,07 dBi, also diesmal ein Gewinnanstieg. Einen Gewinnverlust gibt es auch bei einer mit 12,2 m offener Zweidrahtleitung gespeisten Dipolantenne im Freiraum, deren Schenkel 4,26 m lang sind: Der Gewinn sackt von 2,53 dBi (bei 5 Segmenten) auf 1,48 dBi (bei 50 Segmenten) nach unten durch. Diese abfallenden Gewinne sind in Bild 5 zusammengefasst. Mein weiteres Suchen stollt darn auf die Tatsache, doss bei derselben Antenne fiir die Speisung mit 50Ω-Kabel auch das Minimum der Welligkeit, gemeinhin als Resonanzfrequenz bezeichnet, in seiner Frequenz nicht konstant ist. Mit steigender Zahl der Segmente erhoht sich die Frequenz (Bild 6).
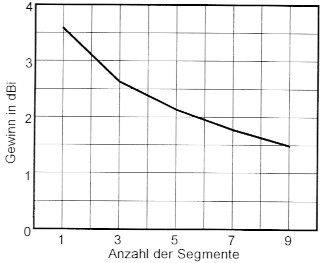
Bild 4: So geht der mit EZNEC errechnete Gewinn einer λ/4-GP mit der Anzahl der Segmente zurück.
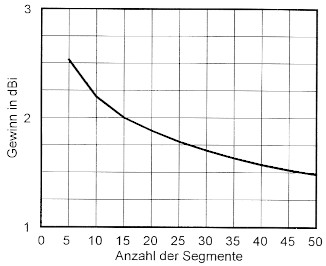
Bild 5: Gewinnrückgang mit der Anzahl der Segmente bei einer Dipolantenne.
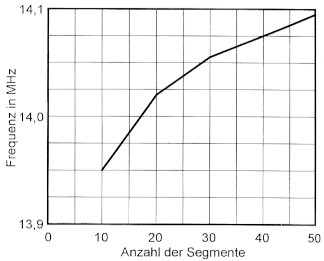
Bild 6: Anstieg der Resonanzfrequenz fur 50 Ω mit der Segmentanzahl bei einer Dipolantenne.
Das Peinliche an den mit der Zahl der Segmente schwankenden Ergebnissen ist, dass es keinen Hinweis gibt, welches Ergebnis richtig ist, oder doch wenigstens, welches Ergebnis wohl dem richtigen Wert nahe ist. Das bleibt völlig im Dunkeln. Resultate, die mit nur einem Segment berechnet worden sind, werden kaum sehr treffend sein; und es bleibt die qualende Frage, wie viel Segmente wir wahlen sollen. Eine kurze Analyse der in EZNEC 2000 enthaltenen fertigen Antennenprogramme führt zu dem Ergebnis, dass Roy Lewallen seine Segmentzahl meist im einstelligen Bereich halt; nur selten wahlt er 11 Segmente. So könnte es gut sein, mit funf Segmenten zu rechnen, doch ist dies rein Spekulation. Hier muss vom Autor noch einige Aufklärungsarbeit geleistet werden.
Die Aufgliederung des Strahlers (und auch der Radials) in Segmente erfordert vom Anwender eine erhöhte Aufmerksamkeit, sollen nicht unwirkliche Ergebnisse herauskommen. Die Rechenzeit steigt quadratisch mit der Menge der Segmente, ist aber bei EZNEC 2000 noch nicht sehr ausgedehnt, aber einige lange Sekunden sind es doch. Auf eine weitere Fehlerquelle werde ich durch(3) aufmerksam gemacht: EZNEC legt den Speisepunkt Milner in die Mitte eines Segments. Hat der Strahler einer Vertikalantenne nun vier Segmente, so liegt die Speisestelle in der Mitte des untersten Segments, siehe Bild 7, obwohl bei "Source" programmiert wurde, dass sie am untersten Ende des Strahlers liegen muss. Diesem Missstand entgehen wir durch einen kleinen Trick: Das unterste Stuck des Strahlers wird nur 2 cm hoch gemacht. Nun legt EZNEC die Speisestelle auf 50 % dieses Stückes. Damit liegt der Speisepunkt 1 cm über dem Anschlusspunkt des Groundplane-Netzes, und das entspricht sogar der Praxis; denn von der Buchse zum Anschluss der Radials fiihrt fast immer ein Draht, bei vomehmen Leuten ein Streifen Kupferblech.

Bild 7: Der Speisepunkt im untersten Segment. Dieses muss moglichst klein gemacht werden.
Obschon die EZNEC-Resultate von der Segmentzahl abhangig sind, haben wir im folgenden diese Schwierigkeit elegant umschiffl: Beim Vergleich zweier Antennen hebt sich die Abhängigkeit heraus; denn es wird immer mit der selben Zahl der Segmente gerechnet. Wir rechnen nicht mit absoluten, sondern mit relativen Gewinnen; denn mit diesen Zahlen lasst sich mit Bestimmtheit sagen, welche Antenne die bessere ist.
Drei Groundplane-Antennen und die klassische Theorie
Es gibt drei grundlegende Modelle der Groundplane-Antennen, die sich nur durch die Höhe ihres Vertikalstrahlers unterscheiden. Die Groundplane bleibt immer gleich: vier Radials von je λ/4 Lange, horizontal verspannt in zwei Meter Höhe über dem Erdboden, dies zeigt Bild 8. Wir wahlen 14 MHz als Frequenz und bekommen dann die Abmessungen in Tabelle 2.
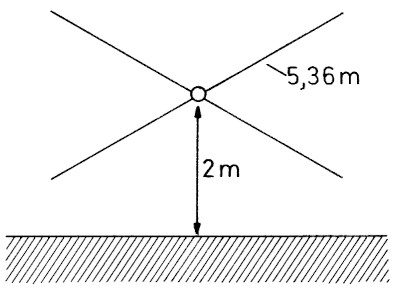
Bild 8: Vierdri:ihtige Groundplane zwei Meter über Grund.
| λ/4-GP | λ/2-GP | λ5/8-GP | |
|---|---|---|---|
| Hohe des Strahlers: | 5,36 m | 10,70 m | 13,40 m |
| Länge eines Radials: | 5,36 m | 5,36 m | 5,36 m |
| Hobe der GP U. Erde: | 2,00 m | 2,00 m | 2,00 m |
| Dicke des Strahlers: | 30 mm | 30 mm | 30 mm |
| Dicke der Radials: | 2 mm | 2 mm | 2 mm |
Die Groundplane ist in 2 m Hohe über Grund verspannt, einfach deswegen, damit wir noch erhobenen Hauptes darunter hindurch gehen können. (Die in (3) immer angewandte Witte der Groundplane von 4 m resultiert aus der Mlle seines Garagendaches.) John D. Kraus, W8JK,(4) hat zu drei entsprechenden Antennen die Feldstarken berechnet. Diese sind wie die Groundplane-Antennen ebenfalls Vertikalstrahler, aber mit dem Unterschied, dass sie nicht auf einer vierdrahtigen Groundplane aufstehen, sondern unmittelbar auf dem ideal leitenden Erdboden. Es sind demnach Monopole (MP). Aus den Kraus'schen Berechnungen ergibt sich unmittelbar der Gewinn in dB fiber λ/4-MP, siehe Tabelle 3.
| λ/4-MP | λ/2-MP | λ5/8-MP | |
|---|---|---|---|
| Feldstarke | 195 mV/m | 236 mV/m | 276 mV/m |
| Gewinn über λ/4-GP | 0 dB | 1,66 dB | 3,02 dB |
Zunachst demonstrieren wir die drei Groundplane-Antennen im Bild. Bild 9 stellt uns die Grundform der λ/4-Groundplane-Antenne vor: Samtliche Leiter sind eine Viertelwelle lang, die vier waagerechten Leiter der Groundplane ohnehin und der Strahler. Der Strombauch des Strahlers liegt unmittelbar über der Groundplane, die als Widerpart die gleiche Stromstarke mit umgekehrter Phase auf die vier Radials verteilt, so dass jedes Radial ein Viertel des Stromes erhalt. Der offensichtliche Nachteil ist in dem tief liegenden Strombauch zu sehen. Die Vorteile sind die Stromspeisung im Fullpunkt und die Stromresonanz der gesamten Antenne, so dass bei einigen Bemiihungen mit 50Ω-Kabel gespeist werden kann.
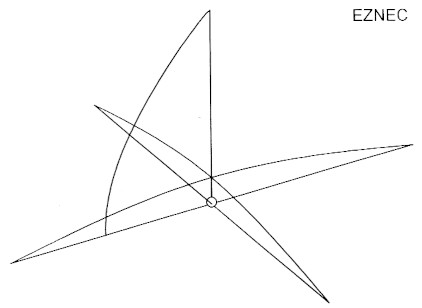
Bild 9: λ/4-GP mit Stromverteilung.
Die Halbwellen-Groundplane ist auf Bild 10 zu sehen. Der ausgeprägte Strombauch ist urn eine Viertelwelle höher gerückt. Nach der Sinustheorie miisste der Strom am Einspeisepunkt I = 0 sein. Es fließt dort aber trotzdem ein erkennbarer Strom, der gegenphasig von der Groundplane aufgenommen und auf vier Teile vergeben wird. Durch die Spannungsspeisung ist der Strom im Fußpunkt, verglichen zur Viertelwellen-Groundplane deutlich geringer, was auch an den Radials gut festzustellen ist. Der Vorteil liegt im erhohten Strombauch, die Nachteile liegen im mechanisch doppelt so hohen Strahler und in der Spannungsspeisung, die durch die Antiresonanz erzwungen ist. Der hochohmige Fußpunktwiderstand erfordert zum Anschluss an das 50Ω-Kabel ein Anpassglied.
Bild 10: λ/2-GP mit Stromverteilung. Die Radialstrome sind viel schwacher als bei der λ/4-GP durch die hohe Speiseimpedanz.
Bild 11 prasentiert uns die λ5/8-Groundplane-Antenne. Auf der gewohnten Ground-plane steht der 0,625-λ-Strahler. Der Strombauch ist noch höher gerückt, so hoch, dass der nachste Teil der Sinuswelle unten deutlich zu sehen ist. Der Sinustheorie folgend müsste der Strom zwischen beiden Halbwellen auf Null zuruckgehen. Weil jedoch die Energie von unten nachgeschoben wird, existiert dort nur ein Stromminimum. Die vier Radials der Groundplane nehmen wieder den FuBpunktstrom auf und zwar in entgegengesetzter Phase. Zwischen Fußpunkt und 50Ω-Kabel muss ein Anpassglied geschaltet werden, das oft nur aus einer Spule besteht.

Bild 11: λ518-GP mit Stromverteilung. Die Halbwelle 1st nach oben verschoben.
Große Unterschiede der drei Groundplane-Antennen
FÜr die weiteren Untersuchungen haben wir das 10,1-MHz-Band ausgewählt, den Strahler mit 30 mm und die Radials mit 2 mm Durchmesser in Kupfer festgelegt. Jeder Leiter bekommt 31 Segmente und die vier Radials liegen fiber normaler Erde. Die Hobe der Groundplane wurde schrittweise gesteigert, beginnend bei z = 0,1 m, endend bei z = 10 m. Errechnet wurden der Gewinn und die Erhebung des Strahlungsmaximums über dem Horizont, die Elevation.
Viertelwellen-Groundplane-Antenne: Bild 12 sagt alles. Mit der Erhohung senkt sich die Elevation von 26° auf 14°. Sie wird also mit der Hobe immer besser fair den Weitverkehr. Der Gewinn ist in Bodennahe ziemlich mickrig und nimmt bei z = 9 m ein Maximum ein. In Wellenlangen ausgedriickt tritt das Maximum bei z = 0,303 λ auf.
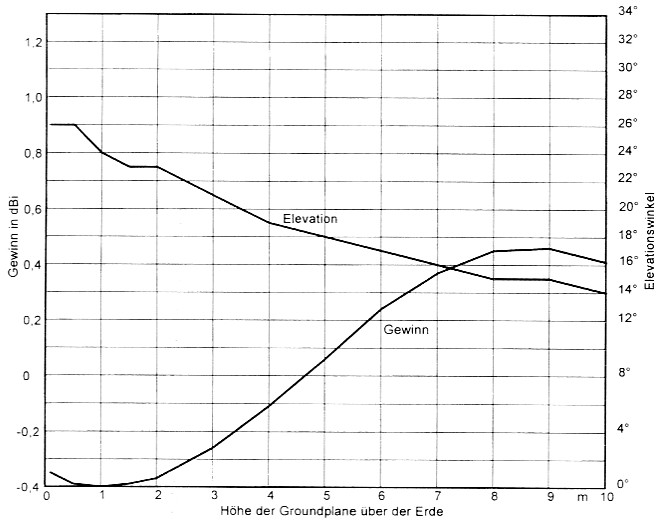
Bild 12: λ/4-GP fur 10,1 MHz. Gewinn und Elevation des Maximums.
Halbwellen-Groundplane-Antenne: Das Diagramm von Bild 13 offenbart die Fakten: Auch bei niedrigster Höhe ist die Elevation mit 20° betrachtlich besser, sie geht sogar bis auf 13° zuriick. Der Gewinn ist schon in Bodennahe besser und steigert sich bis zum Maximum bei z = 7 m, das ist in Wellenlangen z = 0,236 λ, also wenn die Groundplane ungefahr in X/4 Hohe gespannt ist. Auffallend ist der Bruch bei z = 2 m. Dort hate sich bei Erhohen die Resonanzfrequenz der Antenne von 10,1 MHz auf 10,4 MHz verschoben, so dass zur Korrektur der Strahler verlangert werden musste, um wieder auf 10,1 MHz Resonanz zu ergeben. Es ist interessant, dass sich im Gegensatz daze die Resonanzfrequenz bei der λ/4-GP wahrend der gesamten Erhohung nur von 10,1 MHz auf 10,2 MHz verschoben hat. Die λ/2-GP ist also mit der Erde weft weniger verkoppelt, was durch den geringeren Strom in den Radials leicht zu erklaren ist.
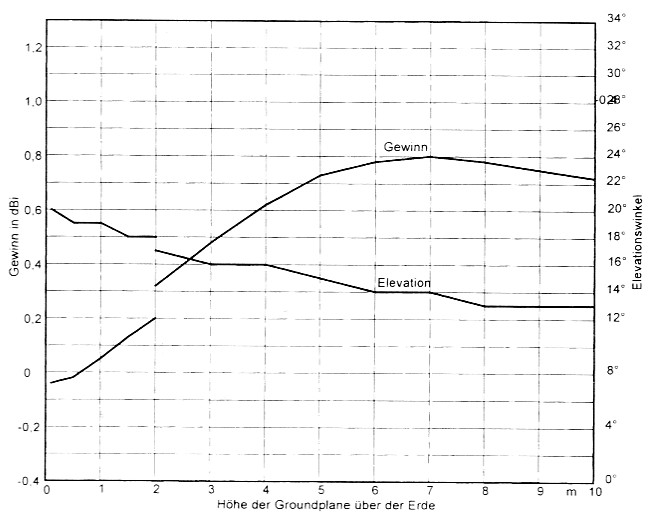
Bild 13: λ/2-GP fur 10,1 MHz. Gewinn und Elevation des Maximums. Bei z = 2 m musste der Strahler verlängert werden, um wieder bei 10,1 MHz Resonanz zu bekommen.
5/8-λ-Groundplane-Antenne: Bei der Fünf-Achtel-Lambda-GroundplaneAntenne ist nach Bild 14 alles anders: Die Elevation ist mit 15° schon in Bodennahe sehr flach und damit für den Weitverkehr günstig. Selbst bei großer Halle (z = 10 m) senkt sich der Elevationswinkel nur noch geringfiigig auf 13°. Der Gewinn hat bereits in Bodennahe sein Maximum. Zu unserer Uberraschung geht der Gewinn bei Erhohung sogar zuruck, um erst bei sehr großer Höhe (z > 10 m) wieder ein weiteres Maximum zu erreichen. Ein wahrhaft günstiges Ergebnis, das alle anderen Übertrifft. Der einzige Nachteil ist, dass die Antenne erheblich höher als ihre Konkurrenten ist, und sie weder in Resonanz noch in Antiresonanz schwingt.
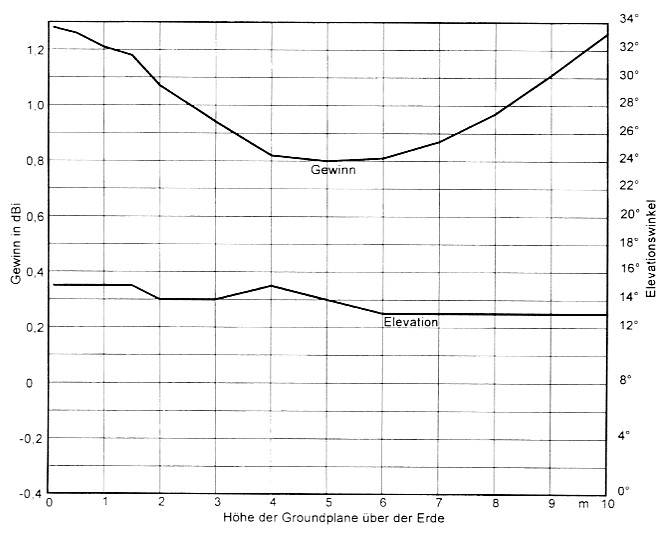
Bild 14: λ5/8-GP fur 10,1 MHz. Gewinn und Elevation des Maximums. Wichtigste Tatsache: Schon in Bodennähe höchster Gewinn!
Die Art der Abstrahlung der drei Groundplane-Antennen wurde diesmal auf 14 MHz untersucht, wo sich zu 10,1 MHz keinerlei merkliche Unterschiede zeigten. Bild 15 zeigt uns das Vertikaldiagramm der λ/4-GP. Die Abstrahlkeule ist breit, der Gewinn ist niedrig und die Elevation ist hoch. Bild 16 bringt das Vertikaldiagramm der λ/2-GP. Die Elevation ist flacher geworden, die Abstrahlkeule schlanker: hoherer Gewinn. Storend ist der "Kamelbuckel" auf der Keule. Schott ware es, wenn man ihn vermeiden konnte; aber so ohne weiteres geht das nicht. Bild 17 zeigt uns das Vertikaldiagramm der λ-5/8-GP.Die Elevation ist auf 14° weiter zuriick gegangen, der Gewinn ist noch etwas angestiegen. Der "Kamelbuckel" hat sich leider noch verstarkt. Aber die Antenne ist trotzdem für DX gut geeignet.
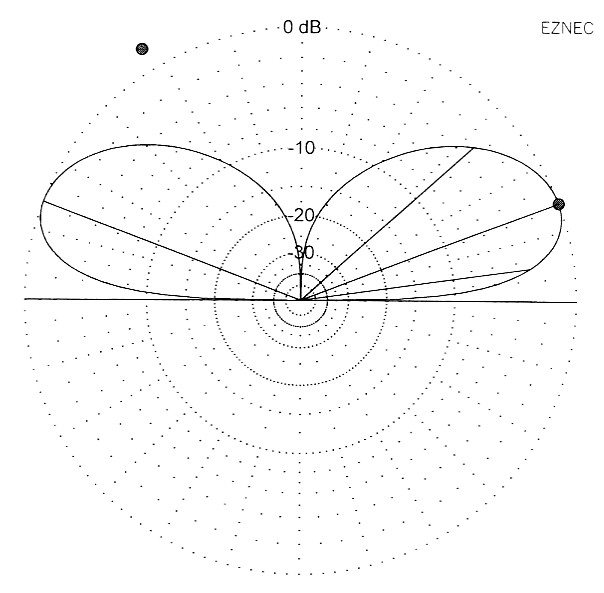
Bild 15: λ/4-GP, Vertikaldiagramm.
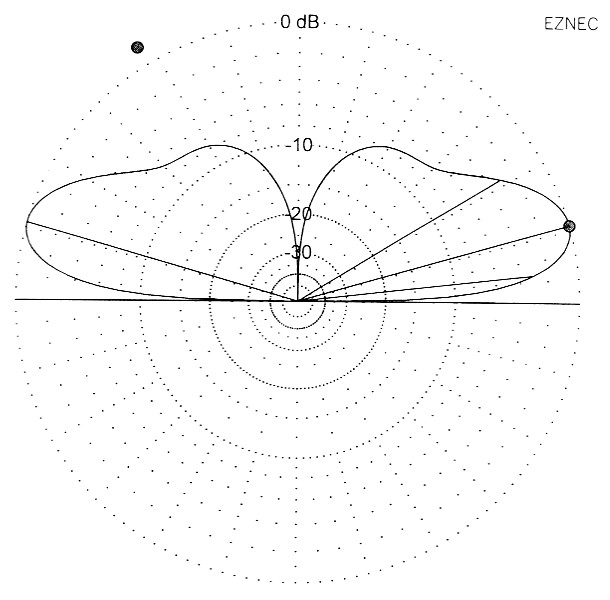
Bild 16: λ/2-GP, Vertikaldiagramm. Der "Kamelbuckel" bewirkt Steilstrahlung.
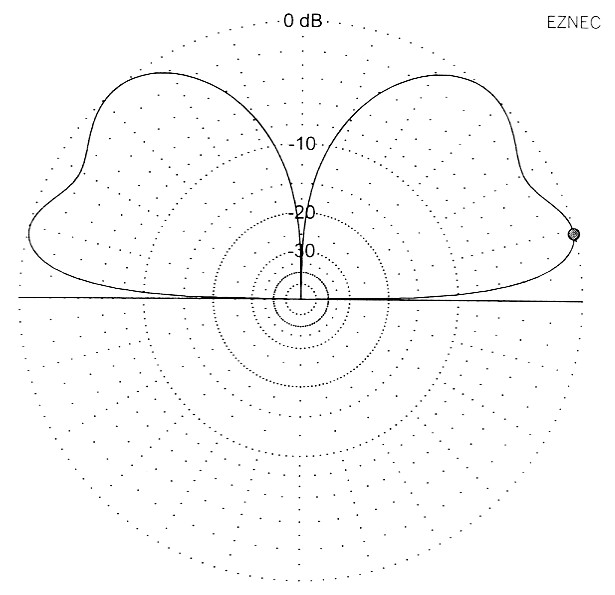
Bild 17: λ5/8-GP, Vertikaldiagramm. Der "Kamelbuckel" ist noch gewachsen, aber der Gewinn in 14° Elevation am graten.
Wenn ich personlich die Wahl ureter den drei GP-Antennen hate, so wurde ich wahrscheinlich die Halbwellen-Groundplane wahlen - aus folgenden Grunden: Der Strahler ist nicht gar so hock und die Strahlungskeule verhaltnismaßig Hach. Freilich müsste ich im Gewinn gegenüber der λ5/8-GP auf ein wenig verzichten.
Kehren wir zu den Bildern 12; 13; 14 zurück, dort sind die optimalen Gewinne mit 0,46 dBi, 0,80 dBi und 1,28 dBi angegeben. Um den Gewinn gegenüber der λ/4-GP als Vergleichsantenne zu erhalten, miissen wir von jeder Gewinnzahl these 0,46 dB subtrahieren. Damit ergeben sich die Werte in Tabelle 4.
| λ/4-GP | λ/2-GP | X5/8-GP | |
|---|---|---|---|
| Urspriinglicher Gewinn: | 0,46 dBi | 0,80 dBi | 1,28 dBi |
| Gewinn über λ/4-GP | 0,00 dB | 0,38 dB | 0,82 dB |
Gegenüber den Berechnungen von W8JK erscheint dies wenig. Das kommt daher, weil wir jedes Mal den maximalen Gewinn genommen haben, der entsteht, wenn sich die Antenne in ihrer optimalen Höhe befindet. Damit konnten die Antennen ihren Gewinn an die beste Antenne annahern.
Verbesserungen an Groundplane-Antennen
Bei der λ/4-GP lasst sich der Gewinn dadurch vergroßern, dass wir den Strahler verlangern. Dadurch nahem wir uns der λ/2-GP und das ist nichts Neues. Wenn der Strahler etwa 0,29 lang wird, ist der Fußpunkwiderstand induktiv, weil der Strahler zu lang ist. Die induktive Komponente konnen wir durch Einschleifen einer Kapazitat des gleichen Blindwiderstandes vollkommen kompensieren, so dass die Fußpunktimpedanz ein reiner Wirkwiderstand ist. Das Schonste daran ist, dass die FuBpunktimpedanz urn die 50 Ω betragt, also unmittelbar mit 50-Ω-Kabel eingespeist werden brut.
Wir haben uns die Miihe gemacht, eine λ5/8-GP für zu optimieren urn den hochst moglichen Gewinn zu erreichen. Die vier Radials schweben in 2 m Hohe über Gartenboden (ε = 13, σ = 0,005), alle Radials und auch der Strahler bestehen aus 2 mm Kupferdraht. Der Strahler hat 1 + 7 Segmente, wobei das unterste 2 cm hohe Segment in seiner Mitte gespeist wird. Die Radials bestehen aus fünf Segmenten, so dass die GP insgesamt 28 Segmente hat. Die Arbeitsfrequenz ist 14 MHz. Die Lange der Radials beeinflusst merklich den Gewinn, wie Bild 18 ausweist. Ihre optimale Lange betragt 5,5 m, das sind 0,2567 λ. Der Strahler nimmt auf den Gewinn wesentlich scharferen Einfluss, was wir an der spitzen Gewinnkurve gut sehen konnen. Eine Feinoptimierung ergab eine beste Lange von 13,15 m Höhe über der Groundplane, das sind 0,6137 λ, also wesentlich weniger als die theoretischen 0,64 λ und auch weniger als λ5/8 = 0,625 λ. Bei h = 15 m wird die Strahlung immer steiler, so dass wir dort die Optimierung beendet haben (Bild 19). Der Gewinn dieser GP hangt sowohl von der Radiallange als auch von der Strahlerlange ab. Deshalb wurde wechselseitig optimiert: erst die Lange der Radials, dann die Lange des Strahlers. Nach zwei Durchgangen blieben die Gewinne stabil. Bild 20 zeigt die Abmessungen der auf Gewinn optimierten λ5/8-GP. Bild 21 stellt das Vertikaldiagramm der Abstrahlung dar. Die Gewinne sind wesentlich höher als bei den vorangegangenen Beispielen bei 10,1 MHz, weil wir diesmal mit weniger Segmenten gerechnet haben.
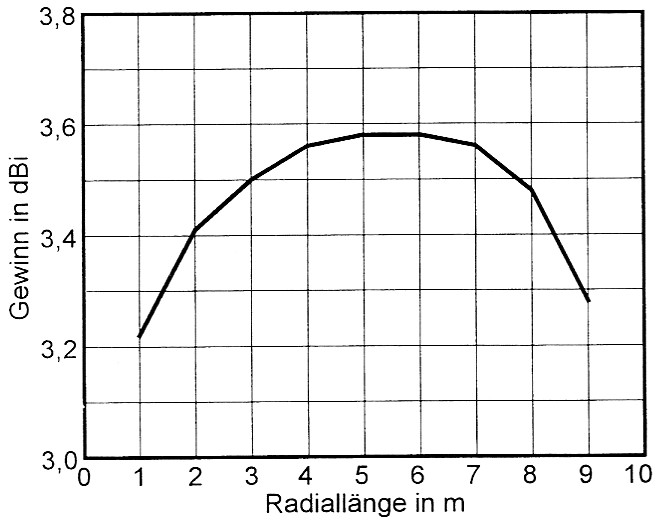
Bild 18: So hangt der Gewinn einer 14-MHz λ5/8-GP von der Lange der Radials ab.
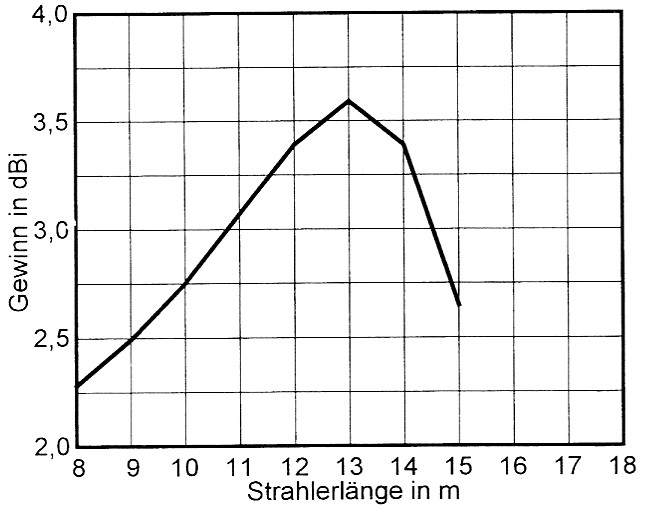
Bild 19: So beeinflusst die Strahlerkänge den Gewinn.
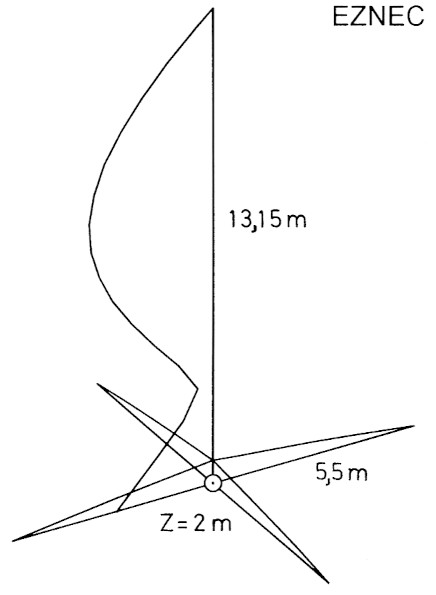
Bild 20: Die optimierte λ5/8-GP für 14 MHz mit ihren Maßen und den Stromen. Die Groundplane liegt zwei Meter über Grund.
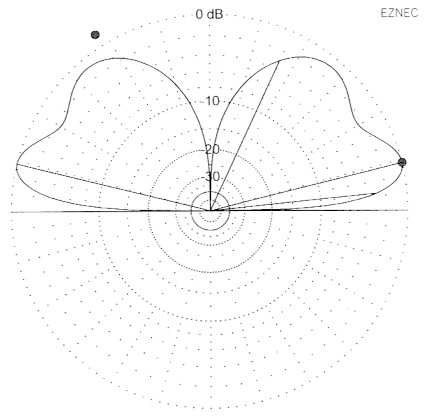
Bild 21: Vertikaldiagramm der optimierten λ5/8-GP.
Zusammenfassung
Alle Groundplane-Antennen sind aus Vertikaldipolen entstanden, deren unterer Schenkel umgestaltet worden ist. Eine Groundplane aus vier Radials arbeitet so gut wie eine viel aufwendigere Erdung. Die λ5/8-GP hat bereits in Bodennahe ihr Gewinnmaximum. Bei der Berechnung dieser Antennen mit EZNEC 2000 ist groBe Vorsicht angebracht, besonders was die Aufgliederung in Segmente und den errechneten Gewinn betrifft.
Karl H. Hine, DL1VU.
Literatur und Quellen
- J. W. Worobjow, Die Momentenmethode in der angewandten Mathematik, VEB Deutscher Verlag der Wissenschaften, Berlin 1961
- R. F. Harrington, Field Computation by Moment Methods, Macmillan, New York 1968
- G. Janzen, DF6SJ, Monopolantennen und Vertikalantennen, Eigenverlag, Hochvogelstrale 29, 81435 Kempten, 1999, hier Seite 79 ff.
- John D. Kraus, W8JK, Antennas, McGraw-Hill, New York, 1950, Kier Seite 311