Antennenanpassung und Smith-Diagramm 2: Amateurband-Losungen
Die Beispiele aus Teil 1 für eine einzige Frequenz ergaben mitunter sehr kleine Werte fur die Anpasselemente. Nun ist aber Amateurfunk nicht auf eine einzige Frequenz beschrankt. Untersuchen wir einmal eine Antenne fur den Betrieb auf 14 bis 14,35 MHz!
Impedanzen außerhalb Widerstands- und Leitwertkreis
Die bisherigen Beispiele ergaben immer eindeutige Lösungen für eine Konfiguration mit L und C. Die Impedanzen lagen stets innerhalb entweder des Leitwert- oder des Widerstandskreises. Liegen die Impedanzen außerhalb, so ergeben sich zwei durchaus praktikable zusatzliche Losungen. So konnen bei der Transformation der Impedanz (30+j40) Ohm bei 10,1 MHz sowohl Widerstands- als auch Leitwertkreis zweimal geschnitten werden. In den Bildern 1 und 2 steht WK für Widerstands- und LK für Leitwertkreis, u für den unteren und o für den oberen Schnittpunkt. 1m Bild 2 ist die genannte Situation dargestellt. Auf die Darstellung der jeweiligen Diagramme wurde bewusst verzichtet, denn das würde den Rahmen sprengen. Unter HAMshelp\Diagramme sind diese beiden Beispiele als ham07a.smc bis ham07d.smc und ham08a.smc bis hamO8d.smc zu finden.
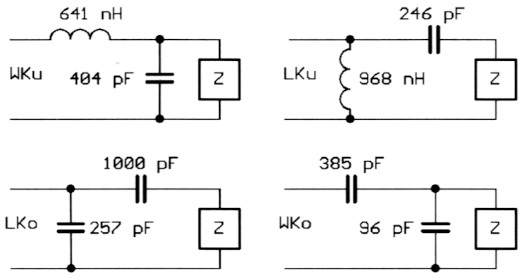
Bild 1: Die vier Losungen für Z = (30 + j40) Ohm
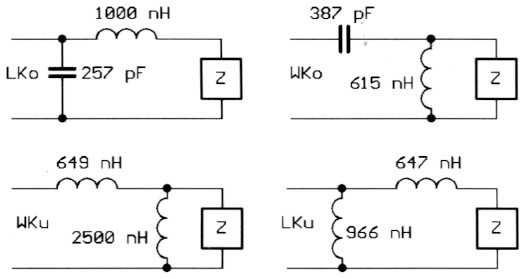
Bild 2: Die vier Losungen für Z = (30 - j40) Ohm.
Die beiden zusätzlichen Anpassvarianten konnen durchaus in der Praxis beim Betrieb in einem geringen Frequenzbereich hilfreich sein. Man erkennt aber auch, dass die Position der Impedanz im Smith-Diagramm stets beachtet werden muss.
Betrieb auf 20 m
Die Anpassung kann in der Regel nur unmittelbar hinter dem Transceiver erfolgen. Gemessen wurde also unmittelbar am Koaxkabel im Stationsraum. Es soil im gesamten 20m-Band durch eine einzige Konfiguration angepasst werden.
Die Demoversion erlaubt einen Startpunkt (DP1) und maximal fünf Datenpunkte DP2 bis 6. Deshalb wurden fünf Frequenzen gleichmaßig verteilt, mit einer Rauschbracke ergaben sich folgende Messwerte:
14.025 kHz: Z1 = (28,4-j28,4) Ohm
14.100 kHz: Z2 = (27-j14,2) Ohm
14.175 kHz: Z3 = (30+j7) Ohm
14.250 kHz: Z4 = (37+j19,2) Ohm
14.325 kHz: Z5 = (43+j22,7) Ohm
Wir tragen die fünf Messpunkte als DP1 bis 5 sowie die Frequenz in ein neues Smith-Diagramm ein. Unter "Options" wird "Connect Datapoints" eingeschaltet. Nun ergibt sich das Bild 3 (s. auch ham10.smc).
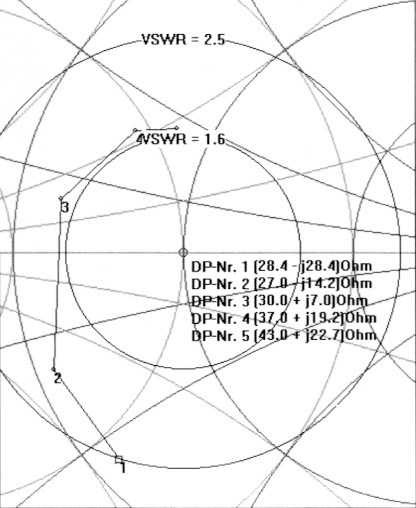
Bild 3: Die Loge der Messwerte der 20-m-Antenne.
Sollten die VSWR-Label storen, kann man sie in ham10.smc mit "Options", "Labels" ausschalten. Schiebt man jetzt den Cursor auf die fünf Datenpunkte, so lässt sich unten das VSWR im jeweiligen Datenpunkt ablesen. Das Maximum liegt bei 14.025 kHz mit 2,5, das Minimum bei 14.325 kHz mit 1,6. Zur Übersicht lassen sich mit "Tool", "Circles", VSWR ... die beiden VSWR-Kreise 2.5 und 1.6 einfügen, wie in Bild 3 sichtbar. Der Kurvenverlauf lasst vermuten, dass Resonanz zwischen 14.025 und 14.100 kHz vorliegt. Allerdings ist der Wirkwiderstand (sichtbar in ham10.smc) nur 30,4 Ohm entsprechend s = 1.6. Hätte man mehr Messwerte aufgenommen so ware der Kurvenverlauf feiner, der Wirkanteil wurde erkennbar bei ca. 28 Ohm liegen. Fährt man mit dem Cursor auf diese Punkte, so lassen sich Impedanz und VSWR jeweils unten ablesen. DP4 und 5 liegen in der Nahe des Übergangs Fläche ½ laut der Orientierungshilfe (Teil 1). Wie die obigen Beispiele zeigen, sollten hier kleine Anpasselemente auftreten.
Nun wollen wir Nägel mit Kopfen machen: Ein Tuner für den Bereich 14 bis 14,35 MHz soll aufgebaut werden, das Stehwellenverhaltnis maximal 3 sein. Grundvoraussetzung ist eine der beiden Konfigurationen (seriell L, parallel C oder seriell C, parallel L) mit einer Spule und einem zwischen Ausgang und Eingang umschaltbaren Drehko.
Beispiel 7 und 8: Parasiten!
Wir setzen für die Praxis eine parasitare (Leitungs-)Induktivitat von 100 nH, eine Anfangskapazitat des Drehkos von 20 pF plus eine parasitare Leitungskapazität von 50 pF an. Demzufolge sind in jedem Datenpunkt 70 pF Parallelkapazität und 100 nH serielle Induktivität zu addieren.
Beispiel 7 (Bild 4, ham11a.smc) soil das im Smith-Diagramm verdeutlichen. Zuerst wird in einem neuen Diagramm DP1 via Keyboard eingestellt (re 28.4, im -28.4, f 14.025 MHz). Jetzt folgt "Shunt C". Der Cursor kann nur auf dem Kreissegment verschoben werden. Im Fenster "Schematic" sind je nach Stellung des Cursors verschiedene Kapazitatswerte abzulesen. Wir wahlen 70 pF und klicken mit der linken Maustaste. Es entsteht DP2. Es folgt die serielle Induktivitat 100 nH. Über "Series L" stellen wir sinngemäß ca. 100 nH ein, DP3 ist entstanden. Und den massen wir jetzt wie in den Beispielen 1-6 bearbeiten. Ein serielles L ergibt DP4, das folgende parallele C ergibt DP5 bei (50+j0) Ohm. Im "Schematic"-Fenster sehen wir, dass 485 nH und 277 pF für die Anpassung bei dieser Frequenz notwendig sind.
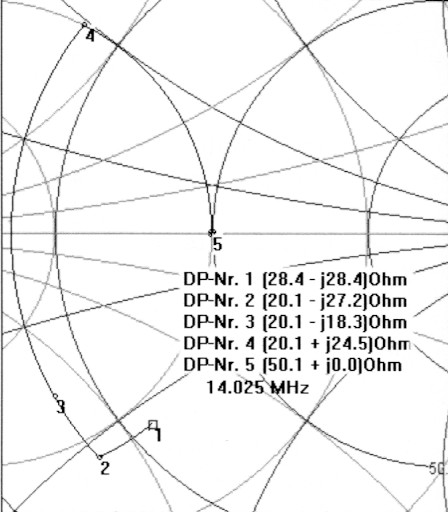
Bild 4: Einbeziehung der parasitaren Blindanteile des Tuners, Messfrequenz 14.025 kHz.
Nun haben wir noch die Lage des Datenpunktes DP5 (für 14.325 kHz) des Bildes 3 zu finden. Wir kontrollieren auch hier den Einfluss der parasitaren Blindanteile.
Wir gehen wie oben vor, siehe Bild 5 (ham12a.smc). Nach dem DP3 wird ein paralleles C von 144 pF erforderlich, das mit seriellen 240 nH kompensiert wird. Jetzt ist zu erkennen, dass zwischen 14.025 und 14.325 kHz die Lage des Kondensators gewechselt werden muss. Werden noch die anderen drei Datenpunkte bearbeitet, sind alle L- und C-Werte bekannt:
14.025 kHz: 277 pF Sender, 485 nH seriell
14.100 kHz: 252 pF Sender, 366 nH seriell
14.175 kHz: 171 pF Sender, 156 nH seriell
14.250 kHz: 140 pF Antenne, 130 nH seriell
14.325 kHz: 144 pF Antenne, 240 nH seriell
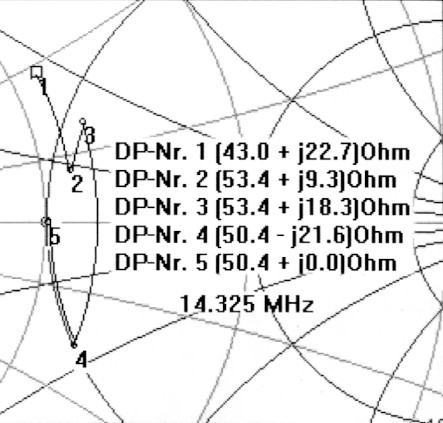
Bild 5: Einbeziehung der parasitaren Blindanteile des Tuners, Messfrequenz 14.325 kHz.
Die C-Variation wird durch einen Drehko 350 pF vollig abgedeckt, L ist problematisch. Entweder man verwendet ein Variometer mit dem Variationsbereich 120 bis 500 nH oder splittet die Induktivitat in zwei Teile. Mit Spulen 200 und 250 nH entstand der Stromlaufplan des Tuners (Bild 6). Das SWR kann damit laut Smith-Diagramm für das gesamte 20-m-Band auf 1,1 bis 1,4 reduziert werden.
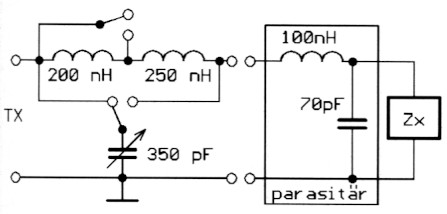
Bild 6: Der aus den Beispielen 7 und 8 resultierende Tuner.
Man erkennt an diesem Beispiel, dass die parasitaren Kapazitaten weitgehend minimiert werden sollten. Gleiches gilt für die Induktivitaten, wobei diese eher beherrschbar sind als die Kapazitaten. Punkt-zu-Punktund Freiluft-Verdrahtung sind hilfreich.
Beispiel 9: feste Induktivitaten
Wie wir gesehen haben, ist das Sorgenkind immer die Induktivität. Man kann hier oft nur feste Werte umschalten. Wie sich das auf das VSWR auswirkt, lässt sich auch mit dem Computerprogramm simulieren. Bild 7 (ham13. smc) zeigt die Option 14.325 kHz mit den parasitaren 70 pF und 100 nH sowie Z = (43+j22.7) Ohm. Wir geben DP1 ein, mit parallelen 70 pF erhalten wir DP2. Die seriellen 100 nH ergeben dann DP3. Das folgende parallele C positionieren wir mit dem Cursor zunächst auf dem Widerstandskreis 50 Ohm. Die Anwahl des seriellen L ergibt einen Kreisabschnitt, auf dem wir nach Kontrolle im Fenster "Schematic" 200 nH (erste Spule) wahlen. Ein Klick erzeugt DP5. Wir liegen neben dem Optimum, aber unser C ist variabel. Wir machen im Fenster "Schematic" einen Doppelklick mit der linken Maustaste auf das in Richtung Sender liegende C, es offnet sich ein Inputfenster. Sie keinnen das Ganze in ham13.smc nachvollziehen, in Bild 7 ist die Kapazitat 120 pF gewählt. Es ergab sich ein s = 1.1. Ein C mit 160 pF schiebt DP5 naher an 50 Ohm reell, die Verbesserung ist aber nur minimal.

Bild 7: Beispiel 9, Endwert mit festem L, hier 200 nH.
Dieses Beispiel wurde gewählt, um bereits vorhandene Induktivitäten als Anpasselement zu prüfen. Variometer sind natürlich besser, meist scheitert aber ihr Einsatz an der Restinduktivität sowie der nicht unerheblichen parasitären Kapazität. Besser wäre eine weitere Spule, nur steigen in diesem Fall auch die zusätzlichen parasitären Kapazitäten. Die Realisierung einer Spule mit z. B. 150 nH ist zudem nicht ganz unproblematisch.
Beispiel 10: ein Trafo
Im Bild 3 war zu erkennen, dass der Wirkanteil der Impedanz im Resonanzfall bei 28 Ohm liegen wurde. Ein unsymmetrischer Übertrager (manchmal auch als Unbal-Unbal oder UnUn bezeichnet) 2:1 ware durchaus machbar, also befragen wir das SmithDiagramm!
Wir öffnen ein neues Diagramm, geben die Impedanzwerte ein (re 28.4, im -28.4, f 14.025) und erhalten DP1, siehe Bild 8 bzw. ham15a.smc. Jetzt aber klicken wir zunachst in der Toolbox den Button "Transf." an. Sichtbar wird ein Kreissegment, das auf beiden Seiten die Begrenzung des Smith-Diagramms verlässt. Auch hier lauft der Cursor immer auf diesem Segment entlang, wir fahren zum Wert 0.5 (entspricht 2:1), der im Fenster "Schematic" angezeigt wird. Nun haben wir DP2. Hier positionieren wir das parallele C 70 pF und die serielle Induktivitat 100 nH. Beim C ist das etwas schwierig, beim L gelingt es besser, aber wir korrigieren beide durch einen Doppelldick auf sie im Fenster "Schematic". In der Inputbox "Change element value" weisen wir ihnen die korrekten Werte zu. Wir haben nun schon DP3 and DP4. DP3 verdeckt DP2 etwas und ist im Bild 8 schlecht zu erkennen. Nahe liegt der obere Leitwertkreis, dorthin fahren wir mit einem seriellen L, wir sind auf DP5. Ein paralleles C beendet in DP6 den Anpassvorgang.
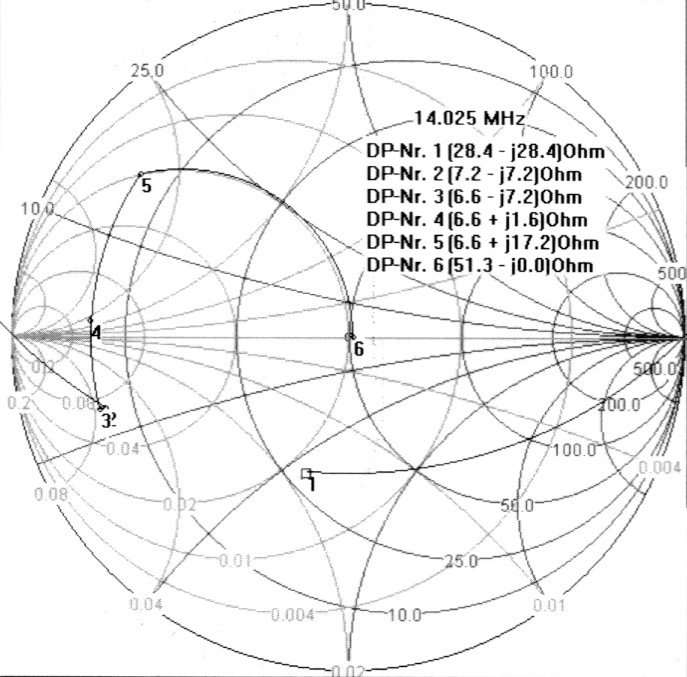
Bild 8: Beispiel 10, Trafoeinsatz.
Berücksichtigt man alle gemessenen Impedanzwerte, so lässt sich mit den Ergebnissen im Smith-Diagramm der in Bild 9 abgebildete Tuner aufbauen. Der Vorteil ist, dass die variable Kapazitat nicht umgeschaltet werden muss, der Nachteil das Variometer. Der Trafo sollte nicht das Problem sein. Aber man sieht, such die Transformation ist nicht von der Hand zu weisen. Mit Probieren ware man nicht auf die Losung des Bildes 9 gekommen.
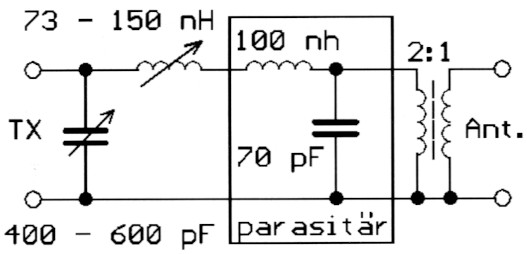
Bild 9: Tuner fur das Beispiel 10 mit Trafo.
Und was ist mit Koax?
Eine gute Frage, denn damit lasst sich einiges aus- und anrichten. Wenig bekannt und genutzt ist im Kurzwellensektor die Tatsache, dass eine Längenänderung des Speisekabels keine Änderung des Stehwellenverhältnisses bewirkt, wohl aber eine Änderung der Impedanztransformation und somit Anpassung. Dass ein VSWR über 1 und Leistungsanpassung keinen Widerspruch bedeutet, erklärt(1). Das Koaxkabel soil als verlustfrei betrachtet werden.
Ein Halbwellenstück beliebigen Wellenwiderstands transformiert 1:1. Man kann durch ein zusatzliches Kabelstrick gleichen Wellenwiderstands, das kürzer ist als eine halbe Wellenlange, dem Tuner eine Impedanz oder einen Impedanzbereich anbieten, den er sicher anpassen kann.
Beispiel 11 (s. Bild 10 bzw. ham16.smc) soll die Impedanzänderung durch eine Längenänderung des Koaxkabels verdeutlichen. Ausgangspunkt ist das Beispiel 8 mit Bild 3. Dazu wird zunachst als DP 1 (dem Startpunkt) eingegeben: re 43.0, im 22.7, f 14.325 MHz. Ein Blick auf die serielle Leitung ergibt einen Vollkreis um den Mittelpunkt, der durch den Punkt DP 1 geht. Der Cursor ist wie üblich auf diesen Kreis fixiert. Um diesen Kreis in der Anzeige im Bild nicht zu storen, wurde der Kreis VSWR = 2.0 eingezeichnet. Nun folgte willkürlich nach der Anzeige im Fenster "Schematic" die Wahl der elektrischen Länge 0.15 λ, Ergebnis ist DP2. Das parallele C von 70 pF ergibt DP3, die serielle parasitäre Induktivität von 100 nH führt zu DP4. Nun wird mit der parallelen Kapazitat transformiert, DP5 entsteht. Die Kompensation mit dem seriellen L ergibt DP6. Damit haben wir wieder Anpassung erzielt, dabei aber mit anderen Lund C-Werten als in Bild 7.
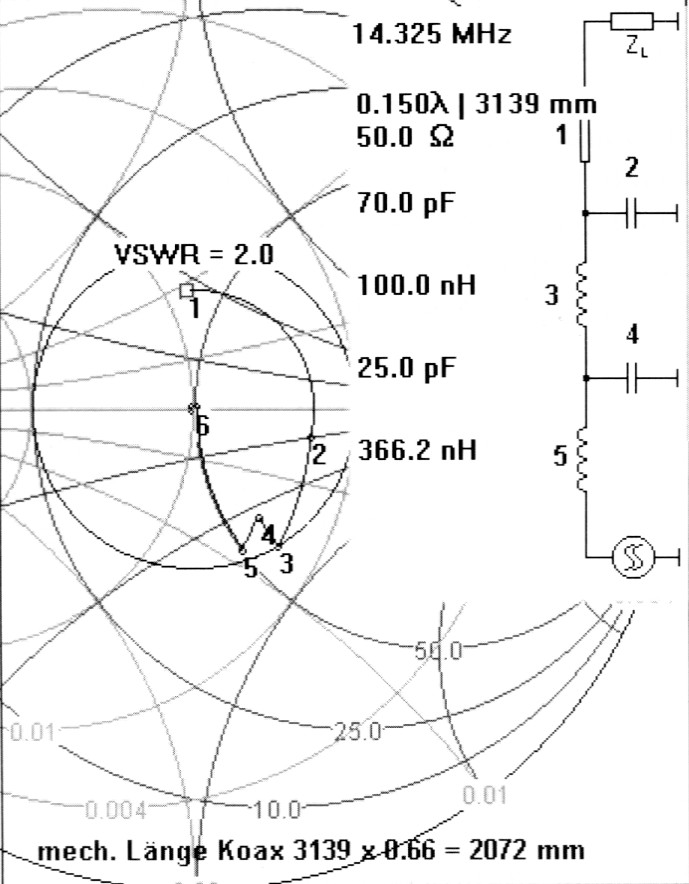
Bild 10: Beispiel 11, Impedanzanderung durch zusatzliches Koaxkabel.
Das Programm gab 3.139 mm Länge an, die mit dem Verkürzungsfaktor zu multiplizieren ist, um zur Länge des zusatzliche Stücks Koaxkabel zu gelangen. Bei RG-58 betragt der Verkürzungsfaktor 0,66. Hieraus ergibt sich die mechanische Länge 2.072 mm.
Im Prinzip ist das impedanzandernde Stuck Koax speziell für den Portabeleinsatz hilfreich. Meist muss man sich sicherheitshalber unterschiedlich Lange zusätzliche Koaxkabel mitnehmen, also kann man damit auch die Impedanzen in den Bereich der optimalen Arbeitsweise des Tuners verschieben.
Antennenimpedanz ermittein
Aus dem oben Gesagten kann man schlussfolgern, dass man mit etwas Geschick auch die Impedanz im Speispunkt der Antenne ermitteln kann. Voraussetzungen sind:
- die gemessene Impedanz am Kabelende
- der Kabel-Wellenwiderstand und
- die elektrische Lange des Speisekabels.
Ist das Kabel elektrisch langer als eine halbe Wellenlänge, dann ist so oft eine halbe elektrische Wellenlänge abzuziehen, bis ein Wert unter λ/2 elektrisch verbleibt. Die subtrahierten Halbwellenstücke transformieren ja 1:1, sind also im Interesse einfachen Vorgehens auszublenden.
Wir versuchen uns am Beispiel 12, Bild 11 (auch ham17.smc). Wir haben ein Koaxkabel 50 Ohm (natürlich verlustarm) mit einer mechanischen Länge von 50 m, Verkürzungsfaktor 0,66, elektrische Länge also 75,76 m (50 m/0,66). Für 3,5 MHz ist die Wellenlänge im Freiraum 85,7 m und im Kabel 56,6 m (85,7 m × 0,66), ein Halbwellenstück also elektrisch 28,3 m (56,6 m/2) lang. Um in den Bereich unter elektrisch λ/2 zu kommen, müssen wir von der gesamten elektrischen Länge (75,75 m) zweimal eine halbe, also eine ganze elektrische Länge (56,6 m) subtrahieren. Das ergibt eine Restlange elektrisch 19,2 m. Das gesamte Kabel transformiert somit wie ein 19,2 m langes Stück.
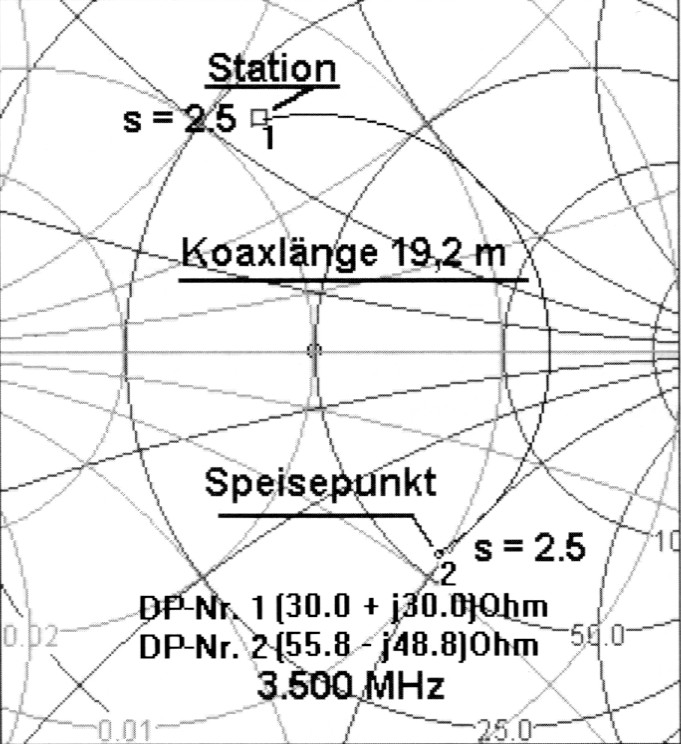
Bild 11: Beispiel 12, Impedanz im Antennenspeisepunkt.
Wir schaffen uns ein neues Smith-Diagramm, Startpunkt DP1 ist re 30, im 30, f 3,5 MHz (ham17.smc). Nun unter Toolbox/Series Line auswahlen: 50 Ohm. Es bildet sich ein Kreis, auf dessen Umfang unser DP1 liegt. Der Cursor lässt sich wie immer nur auf diesem Kreis fahren, wir setzen ihn rechtsdrehend unter Beachtung der Anzeige im Fenster Schematic auf 19200, also 19,2 m. Dort ein Klick, es entsteht DP2. Hier ist die Impedanz laut Fenster DataPoint (55.8-j48.8) Ohm. Würden wir unter Tools/ Circles/VSWR ... den Kreis 2.5 einschreiben, so wurde dieser sowohl durch DP1 als auch durch DP2 gehen. Es hat sich ja am VSWR nichts geändert.
Messvorgang in Kurzfassung: Mechanische Kabellange dividieren durch Verkfirzungsfaktor ergibt elektrische Länge. Davon soviel mal λ/2 subtrahieren, bis maximal λ/2 übrigbleibt. Gemessene Impedanz und Messfrequenz ergeben DP1. Line seriell wählen, elektrischen Restlange einsetzen, ergibt DP2 und die Impedanz im Speisepunkt zu Z = (55.8-j48.8) Ohm bei 3.500 kHz.
Anpassung fur eine spezielle Frequenz
Gerade im 10-m-Band gibt es das Problem, dass man seine Antenne für den CW-Bereich optimiert hat, nun aber doch gelegentlich im hochfrequenten Ende des Bandes arbeiten möchte. Suchen wir also eine Losung mit Koax, die direkt im Speisepunkt der Antenne wirksam werden kann! Das Beispiel 13 (Bild 12, haml8.smc) nimmt an, dass bei 29,5 MHz ein SWR von 6 auftritt. Gemessen am Speisepunkt des Strahlers betragt die Impedanz (24.5-j66.5) Ohm. Schalten wir ein zusatzliches Stuck Koax ein, so verandem wir das SWR nicht, wohl aber die Impedanz. Für den Bandanfang ist das zusatzliche Koaxkabel uninteressant, nicht aber für 29,5 MHz. Wir lösen das Problem mit dem Smith-Diagramm und geben den Startpunkt. DP1 mit re 24.5 und im -66.6 sowie f 29.500 MHz ein. Da wir mit lediglich einem parallelen Bauelement anpassen wollen, müssen wir den Leitwertkreis schneiden. Es gibt zunachst den ersten Schnittpunkt (DP2) bei Z = (9.7-j19.8) Ohm. Ein paralleles L 132 nH ergibt Anpassung. Das zusatzliche Koaxstück ist hier 935 mm × 0,66 = 617 mm lang. Der zweite Schnittpunkt (DP3) bei Z = (9,8+j20) Ohm ergibt ein paralleles C mit 217 pF und eine Koaxlange von 2.199 mm × 0,66 = 1.451 mm. Als praktische Losung bietet sich an, am Beginn des Verlangerungsstucks das Bauelement mittels Relais zuzuschalten. In Bild 13 ist eine solche Moglichkeit für beide Anpassvarianten gezeigt. Im Prinzip einfach, man muss nur wissen, wo man was zuschaltet. Mit "cut and try" ist da nichts mehr zu machen.
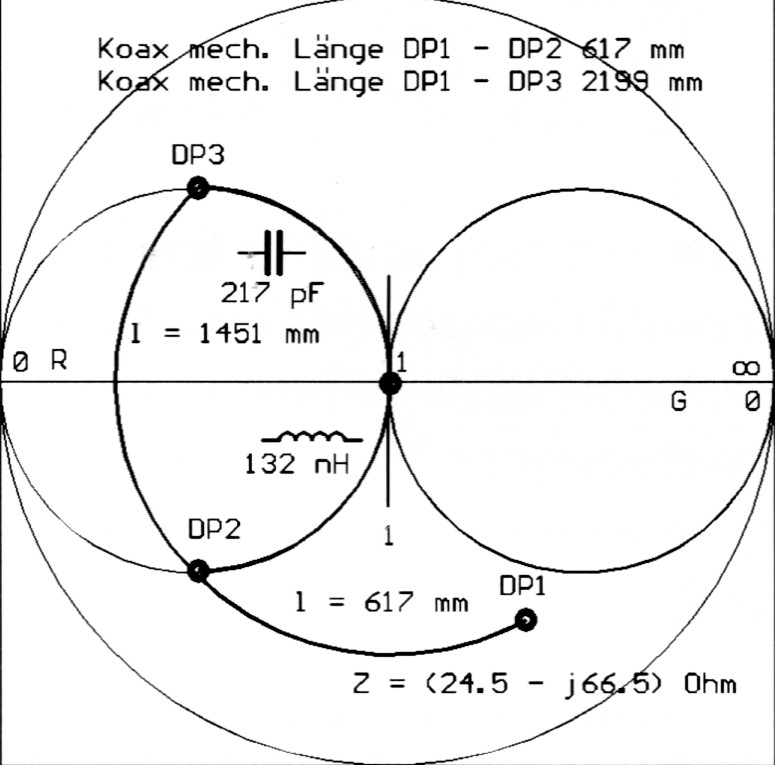
Bild 12: Beispiel 13, koaxiale Verlangerungen.
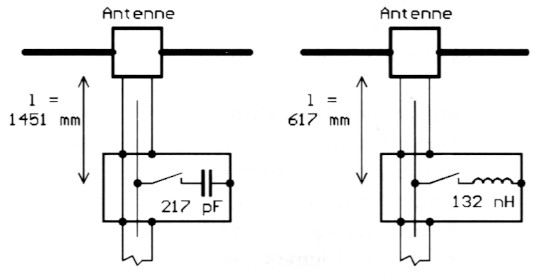
Bild 13: Die Realisierung des Beispiels 13.
Eine weitere Lösung wäre die Verwendung von seriellen Kompensationselementen. Ausgehend vom obigen DP1 bei (24.5-j66.5) Ohm ergabe sich beim ersten Schnittpunkt diesmal mit der Wirkwiderstandsachse eine Koaxlange von 2.287 mm und eine serielle Kompensationskapazitat von 53,7 pF. Beim zweiten Schnittpunkt waren es 3.128 mm und serielle 549 nH.
Man nehme Stubs
Beispiel 13 bietet sich für die Lösung mit Stubs an. Bekanntlich wirkt ein offener Stub wie eine Kapazität, ein geschlossener wie eine Induktivität. Würde man im Bild 10 (bzw. ham18.smc) anstelle der parallelen Induktivität ein Stuck Koaxkabel nehmen, so müsste dieses im DP2 geschlossen und mechanisch 591 mm lang sein, im DP3 offen und 491 mm lang. Die jeweiligen Verlängerungsstücke bleiben aber wie gehabt.
Mit Koax und Drehko
Die Impedanzänderung durch verlängerndes Koaxkabel ermoglicht aber auch noch obskure Anpassvarianten, wir bauen einen Tuner der ganz anderen Art. Bisher haben wird die Transformationselemente stets mit Spule und Drehko aufgebaut, nun nehmen wir als Induktivität Koaxkabel und einen parallelen Drehko.
Ausgangspunkt für die Lösung ist Betrieb auf den Kurzwellenbandern 80 m bis 10 m, ein maximales VSWR von 3 auf dem Koaxkabel im Stationsraum, Anpassung im Stationsraum. Es sind nun solche Koaxstücke zu bemessen, mit denen wir auf alien obigen Bandern das VSWR von 1 weitgehend erreichen. Aus den bisherigen Beispielen wissen wir bereits, dass in der Konfiguration "paralleles C auf der Senderseite, serielle Induktivital auf der Antennenseite" auf dem VSWR-Kreis (hier also s = 3) rechtsdrehend der Schnittpunkt des VSWR-Kreises mit dem Leitwertkreis 0,02 S in der oberen (!) Diagrammhälfte gesucht werden muss. Und nur dann geht dieses hier beschriebene Prinzip. Im ungünstigsten Fall ware rechtsdrehend ein Drehwinkel von 359° erforderlich. Und falls man es vergisst, im Diagramm gibt der kleine Pfeil auf dem VSWR-Kreis die Drehrichtung an.
Für die tiefste Frequenz 3.500 kHz ist λ/2 im Freiraum 42,8 m. Bei Koaxkabel mit einem Verkürzungsfaktor von 0,66 ware die entsprechende Länge 42,8 m × 0,66 = 28,25 m.
Diese teilen wir auf in acht verschiedene binar gestaffelte Langen, beispielsweise 14,1, 7,06, 3,53, 1,77, 0,88, 0,44, 0,22 und 0,11 m. Ihre Summe erreicht fast wieder 28,25 m. Bei s = 3 benotigen wir (entnommen aus dem Smith-Diagramm) bei 3.500 kHz eine maximale Kapazitat von 1.100 pF. Eine mogliche binare Stufung konnte wie folgt aussehen: 1.000, 560, 280, 140, 60, 35, 18 und 10 pF, wobei hier Normwerte eingesetzt werden konnen. Der Stromlaufplan eines solchen Tuners ist in Bild 14 zu sehen. Die Anzahl der Koaxstücke wurde minimiert, die Kapazitat als ein einziger Drehko dargestellt.
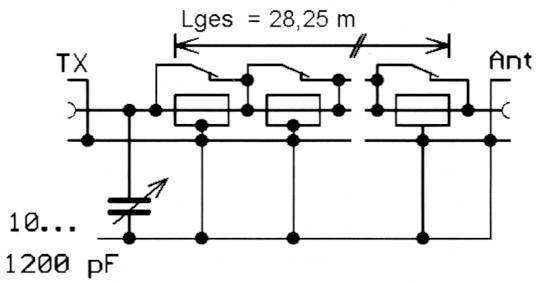
Bild 14: Tuner mit Koaxstücken und Drehko.
Dieser Tuner hat wenig praktischen Wert, denn sein Einsatz im Stationsraum bietet zwar dem Sender eine minimale Fehlanpassung, die Fehlanpassung zwischen Tunerausgang und Antenne mit ihren Verlusten bleibt erhalten. Die theoretisch auch maximal mogliche zusatzliche Koaxlange von ca. 28 m dürfte wegen der Verluste auch nicht das Optimale sein.
Zusammenfassung
Aus den obigen Beispielen kann man erkennen, dass mit etwas Kenntnis and Übung diverse Anpassprobleme mit dem Smith-Diagramm gelöst werden können. Voraussetzung - und das darf man nicht vergessen - ist eine vorherige Impedanzmessung an dem Punkt, an dem man die Anpassung vornehmen will. Die Einsatzmoglichkeiten des Smith-Diagramms sind mit obigen Beispielen nicht erschöpft, dürften aber zumindest für den "Hausgebrauch" hilfreich sein.
Literatur
Max Perner, DM2AUO.