Oberwellenunterdrückung bei Antennenkopplern; Wie stark ist die Dämpfung?

Mit den Arbeiten über das T-Glied als Antennenkoppler haben wir mitten ins Schwarze getroffen. Eine Menge Anfragen und Leserbriefe trudelten in der Redaktion ein. Viele Nachbauer wollten tiefere Einzelheiten wissen. Eine Gruppe kritischer Leser beschäftigte sich mit der Frage, wie stark die Oberwellen des Signals von dem T-Glied gedämpft werden. Dieses Problem ist aktuell, obschon die heutigen Transceiver nicht mehr solche an Harmonischen reiche Frequenzfamilien ausstrahlen, wie es zu leiten der Röhrensender war.
Vollkost aus der Hochfrequenztechnik
Das T-Glied zur Anpassung unterschiedlicher Impedanzen ist meistens als Hochpass geschaltet. Es dämpft such in dieser Schaltung die Oberwellen des Signals, freilich nicht so kräftig wie es ein Tiefpass tun würde, aber die Vielfachen der Grundfrequenz werden doch erheblich herabgesetzt. Wie weft, das ist mit Hilfe fertiger Programme feststellbar; aber erstens ist solch ein Programm meistens nicht greifbar und zweitens kann man nicht beurteilen, ob das Programm richtig läuft oder ob es fehlerhafte Ergebnisse liefert. Da hilft nur eines: Selbst die Tatsachen zu analysieren und sich Durchblick zu verschaffen, und das ist Vollkost aus der Hochfrequenztechnik.
Besonders reizvoll ist dabei die Möglichkeit, sich auf drei verschiedenen Wegen einen Durchblick zu verschaffen. Je mehr die Methode ausgefeilt ist, umso näher kommt das Ergebnis der Wirklichkeit. Unsere drei Lösungswege sind:
- Die Berechnung mit Hilfe des Ohmschen Gesetzes und der Impedanzen, kurz: die Impedanzmethode,
- Die Berechnung unter Berücicsichtigung der Phasenverschiebungen, kurz: die Phasenmethode,
- Die Berechnung mit Hilfe der Vierpoltheorie, kurz: die Vierpolmethode.
Wer jetzt schon das Heft zuschlägt oder zu den Ergebnissen übergeht, hat den Genuss des Denkens und Entdeckens beiseite liegen lassen. Doch bei der Durcharbeitung gibt es einen Trost: Es ist alles mit simplen Überlegungen zu schaffen!
Impedanzen
In der Gleichstromtechnik arbeiten wir mit Widerständen, die mit R bezeichnet werden. In der Wechselstromtechnik werden die Widerstände als Impedanzen angesprochen und mit Z benannt. Sonst ändert sich vorerst gar nichts. Wir unterscheiden Wirlcwiderstände R, welche die elektrische Energie in Wärme umwandeln, z. B. eine Dummyload; Blindwiderstände X, welche zwar Ströme fließen lassen und in der Phase verschieben, aber keine Wärme erzeugen, z. B. ideate Kondensatoren und Spulen, C und L; und wir kennen Scheinwiderstände, Impedanzen Z, die aus Wirk- and Blindwiderständen zusammengesetzt sind, also mit Gleichungen der Art Z = R + jX beschrieben werden können. Der Einfachheit (und der Faulheit) halter kümmern wir uns zunächst gar nicht um die Zusammensetzung, sondern verwenden die Impedanz Z einfach als gegebene, einheitliche Größe.

L-C-L-Tiefpass zu Messzwecken. Die keramischen Spulenkörper stammen aus dem Tornisterempfanger "Berta" und haben trotz ihrer Konstruktion aus dem Jahre 1938 heute noch Spitzenqualität.

C-L-C-Hochpass.
Analyse aus den Impedanzen
Als Ausgangspunkt unserer Überlegungen nehmen wir Bild 1. Es zeigt uns das T-Filter Z1, Z2, Z3 mit dem Lastwiderstand des Antennenkabels ZL. Genau betrachtet ist das T-Filter eine Serienschaltung aus zwei Sparmungsteilern. Der erste besteht aus Z1 and Z3 mit allem, was daran hängt; der zweite setzt sich aus Z2 und ZL zusammen. Am Eingang, der meistens am 50-Ω-Ausgang des Transceivers liegt, herrscht die Spannung U1. An der Querimpedanz Z3 tiff die Spannung U3 auf, und an der Ausgangsimpedanz ZL liegt die Spannung U2. Um die Dämpfung des T-Gliedes für jede beliebige Frequenz zu ermitteln, müssen wir nur das Verhältnis der beiden Spannungen U2/U1 berechnen. Wir gehen das Problem mit ganz einfacher, dorfüblicher Logik an. Dazu brauchen wir noch eine Zwischengröße und definieren Z als die Impedanz, die zwischen A und B liegt. Offensichtlich entsteht Z aus der Parallelschaltung von Z3 und Z2 + ZL. Wir konnen also schreiben:
Z = Z3 || (Z2 + ZL) [1]
Das ergibt ausgerechnet:
Z = Z3 × (ZL+Z2) / (ZL+Z2+Z3) [2]
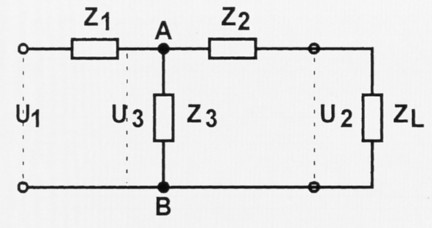
Bild 1: Der T-Koppler aus Impedanzen zusammengesetzt.
Die Spannung U3 liegt zwischen A und B, also an Z. Sie entsteht aus der Spannung U1l an einem Spannungsteiler, der sich aus Z1 und Z zusammensetzt (Bild 2). An Z + Z1 fällt U1 ab, an Z fallt U3 ab.
Also gilt: U3 / U1 = Z / (Z + Z1) [3]
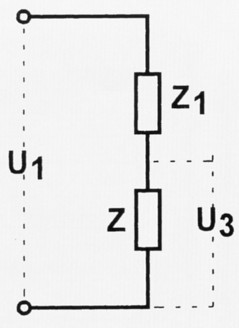
Bild 2: Der erste Spannungsteiler.
Wenn wir Bild 3 betrachten, so sehen wir, dass die Spannung U3 zwischen Z2 und ZL aufgeteilt wird. Die Spannungen verhalten sich proportional wie die Widerstände:
U2 / U3 = ZL / (ZL + Z2) [4]
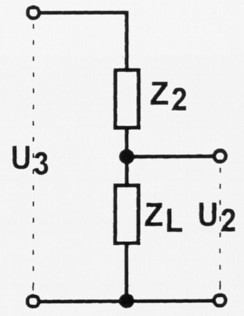
Bild 3: Der zweite Spannungsteiler.
Zuerst berechnen wir U2 aus [4] and erhalten:
U2 = ZL × U3 / (ZL + Z2) [5]
Darauf berechnen wir U3 aus [3]:
U3 = U1 × Z / (Z + Z1) [6]
Nun setzen wir U3 aus [6] in [5] ein und bekommen:
U2 = U1 × ZL × Z / ((ZL + Z2) × (Z + Z1)) [7]
Die Dämpfung wird durch das Verhältnis U2 / U1 beschrieben, und das wird:
U2 / U1 = ZL × Z / ((ZL + Z2) × (Z + Z1)) [8]
Jetzt müssen wir nur noch Z aus [2] einsetzen, und damit wird es kompliziert:
Zähler: U2 = ZL × Z3 × (ZL + Z2)
Nenner: U1 = (ZL + Z2 + Z3) × (ZL + Z2) × ((Z3 × (Z2 + ZL) / (ZL + Z2 + Z3)) + Z1)
Glücklicherweise lässt sich (ZL + Z2) bei Zahler wie Nenner herauskürzen:
Zähler: U2 = ZL x Z3
Nenner: U1 = (ZL + Z2 + Z3) × ((Z3 × (ZL + Z2) / (Z1+ Z2 + Z3)) + Z1)
Dies vereinfacht sich auf:
Zähler: U2 = ZL x Z3
Nenner: U1 = Z3 × (ZL + Z2) + Z1 × (ZL + Z2 + Z3)
Nach Auflösung der Klammern ergibt sich die Dampfung
U2 / U1 = ZL × Z3 / (ZL x Z3 + Z2 × Z3 + Z1 × ZL + Z1 × Z2 + Z1 × Z3) [9]
Dies lässt sich noch vereinfachen zu
U2 / U1 = Z3 /( Z1 + Z3 + (1 /ZL) × (Z1 x Z2 + Z1 × Z3 + Z2 x Z3)) [10]
Jetzt brauchen wir nur noch die einzelnen Impedanzen einzusetzen und erhalten daraus sofort die Dämpfung. Die errechnete Formel [10] ist universal, das heißt, wir konnen als Z1, Z2 und Z3 beliebig die Impedanzen von R, C oder L einsetzen. Sie gilt also für Hoch- und Tiefpass mit beliebigen Schaltelementen.
Analyse aus den Blindwiderstanden
Die Anordnung der Blindwiderstände in einem Hochpass-T-Filter zeigt uns Bild 4. Die beiden Drehkondensatoren sind X1 und X2, die Spule ist X3, und der Lastwiderstand der Antenne ist R. Damit wird X1 = 1 / jöC1; X2 = 1 / jωC2 und X3 = jωL. Der Rechengang ist der gleiche wie bei den Impedanzen schon ausgiebig vorgeführt. Er muss deshalb nicht wiederholt werden. Wichtig ist für uns nur das weitgehend der Formel [11] entsprechende Endergebnis. Darin ist der Operator j nur noch einmal enthalten. Er muss also bei den einzelnen Blindwiderständen nicht mehr angeführt werden:
U2 / U1 = X3 / (X1 + X3 + j × (X1 × X2 + X1 × X3 + X2 × X3) / R) [12]
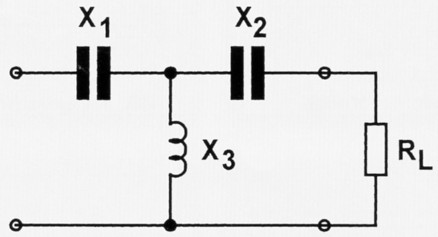
Bild 4: Der T-Koppler aus verlustfreien Blindwiderstanden.
Zur Berechnung werden die zwei Ausdrücke unter dem Bruchstrich nicht arithmetisch sondern geometrisch addiert und daraus die Quadratwurzel (SQR = Squareroot) gezogen, und das ergibt:
U2 / U1 = X3 / √((X1 + X3)2 + ((X1 × X2 + X1l × X3 + X2 x X3) / R)2) [13]
Auch diese Formel ist universal und gilt für Hoch- wie Tiefpassfilter.
Analyse mit der Vierpoltheorie
Die von Richard Feldtkeller entwickelte Vierpoltheorie(1) gibt uns ein ausgezeichnetes Mittel an die Hand, die Betriebsdampfung eines T-Filters zu berechnen, wobei sogar auf den Innenwiderstand der Spannungsquelle Rücksicht genommen wird, der in unserem Bereich fast immer 50 Ω ist. Es gilt Bild 5. Achtung: Die Indizes der Komponenten sind hier anders. Z1 und Z3 sind den Kondensatoren zugeordnet, Z2 der Spule. Für den T-Vierpol gilt dann folgende Vierpolmatrix:
Z = |Z11 Z12||Z21 Z22|
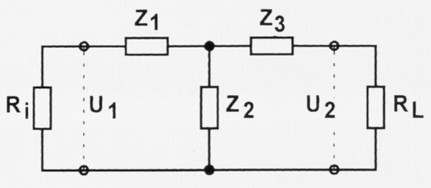
Bild 5: Der T-Koppler als Vierpol.
Darin ist Z11 = jωL + 1/jωc1; Z12 = jωL; Z21 = jωL und Z22 = jωL + 1/jωC3. Nach der Vierpoltheorie ergibt sich daraus sofort das komplexe Betriebsdämpfungsmaß mit(2):
U1 / U2 = egB = ((RL + Z22) × (Ri + Z11) - Z122) / (2 × Z12 × √(Ri × RL)) [14]
Aus dem Betriebsdämpfungsmaß erhalten wir die Betriebsdämpfung in Neper durch den naturlichen Logarithmus: aB =1n(egB) [Np] und daraus die Betriebsdampfung in dB: a = aB[Np] × 8,686. Um diesen Ausdruck für die Rechnung und den PC gerecht zu machen, muss er umgeformt werden, und wir erhalten die Betriebsdampfung mit:
a = 8,686 × In{(1 / (2ωL × √(Ri × RL))) × √[ωL × (Ri + RL) - Ri / (ωC3)- RL/ (ωC1))2 + (1/(ω2 × C1 × C3) - Ri x RL - L/C1 - L / C3)2]} [dB] [15]
Es ware zu viel verlangt, diesen Ausdruck im "Handbetrieb" rechnen zu wollen. Dies ist das ureigene Feld des Computers, der für die Formeln [10], [13] und [15] in GW-Basic programmiert wurde, um die Ergebnisse in Diagramm-Form auszudrucken.
Ergebnisse
Das Verhaltnis U2 / U1 liefert uns als Ergebnis, wieviel Ausgangsspannung U2 durchgelassen wird, wenn die Eingangsspannung U1 beträgt. Es ist der Kehrwert der Dämpfung und kann mit "Durchlass" bezeichnet werden. Das Verhaltnis U1 /U2 ergibt dagegen die numerische Dämpfung, die wie oben durch Logarithmieren in dB umgewandelt werden kann.
Bild 6 zeigt uns den Durchlass eines Hoch-passes (HP) nach der Impedanzmethode. Im Resonanzpunkt ist U2 / U1 gleich unendlich, ein Resultat, das nicht ganz stimmen kann. Trotzdem ist die Resonanzfrequenz, bei der im Wesentlichen Anpassung herrscht, bei 14 MHz recht gut getroffen. Von 0,5 MHz bis etwa 13 MHz und von 16 MHz bis 30 MHz verläuft die Kurve unter 1,0. Das heißt in diesen Bereichen werden Nebenfrequenzen gedämpft, tiefe starker als hohe Frequenzen. Von 13 bis 16 MHz ist der Durchlassbereich.
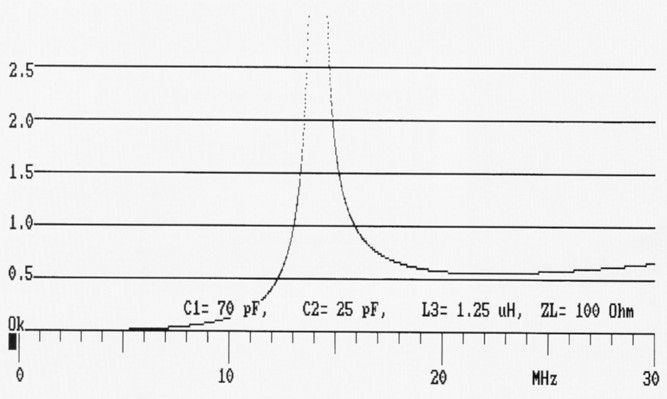
Bild 6: Numerischer Durchlass (HP) nach der Impedanzmethode.
Bild 7 gilt für den gleichen Hochpass C-L-C. Hier ist die numerische Dampfung, also der Kehrwert von Bild 6 dargestellt. Die Eingangsspannung Ul wird also mit der Ausgangsspannung U2 gemessen. Im Resonanzpunkt ist die Dämpfung gleich Null. Liegt sie über 1,0, so ist die Ausgangsspannung geringer als die Eingangsspannung, dort ist der Durchgang gedampft. Frequenzen tiefer als 14 MHz werden stark gedämpft, Frequenzen darüber werden nur noch gering gedämpft, eine Folge der Hochpass-Funktion. Bei etwa 22 MHz hat die Dämpfung ein Maximum, über 22 MHz geht die Dämpfung wieder zurück. Dies ist eine Folge der Kondensatorkette im Filter.
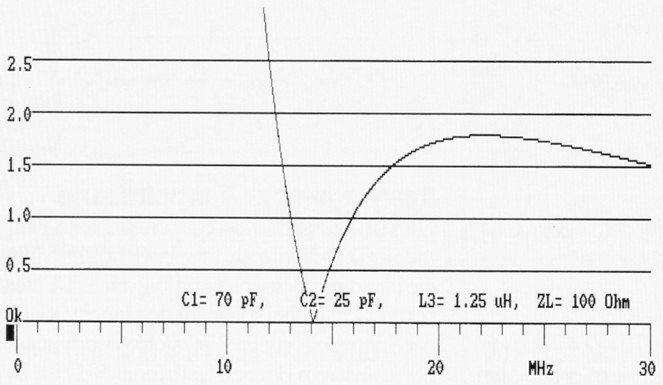
Bild 7: Numerische Dämpfung (HP) nach der Impedanzmethode.
Bild 8 gilt für den Durchlass des gleichen Hochpasses, ist aber mit der Phasenmethode berechnet worden. Es springt sofort ins Auge, dass U2 nicht mehr unendlich wird, sondem nur noch etwa den Wert 3,0 erreicht. Das bezeugt die bessere Interpretation der physikalischen Gegebenheiten. Auch die Resonanzfrequenz ist etwas höher geworden.
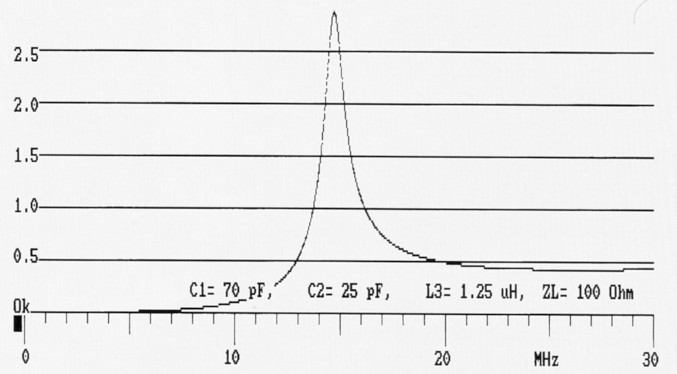
Bild 8: Numerischer Durchlass (HP) nach der Phasenmethode.
Bild 9 zeigt die numerische Dämpfung des gleichen Hochpasses nach der Phasenmethode. Das Minimum der Dampfung bei etwa 14,7 MHz geht nicht mehr auf Null zuruck, das heißt: Das T-Filter dämpft auch die Durchlassfrequenz. Dies lässt sich durch genauere Einstellung beseitigen. In der Praxis werden nun die Cs und das L so lange nachgestellt, bis Das SWR auf 1 zurückgegangen ist. Bei idealen Bauteilen geht die Dämpfung der Arbeitsfrequenz auf Null zurück.
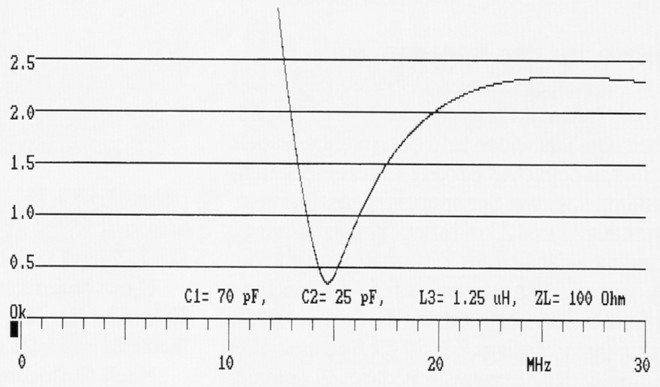
Bild 9: Numerische Dämpfung (HP) nach der Phasenmethode.
Bild 10 gilt abermals für den gleichen Hoch-pass. Es zeigt die Dämpfung dieses T-Filters nach der Vierpolmethode. Wohl gemerkt: Die linke Skala ist in dB angegeben. Bis zu 12 MHz ist die Dämpfung höher als 10 dB. Ab 21,5 MHz ist die Dämpfung rund 4 dB, für die Praxis etwas wenig. Im Durchlassbereich von 15 bis 16 MHz ist die Dämpfung etwa 2 dB, die sich durch bessere Einstellung des T-Filters noch vermindern lässt.
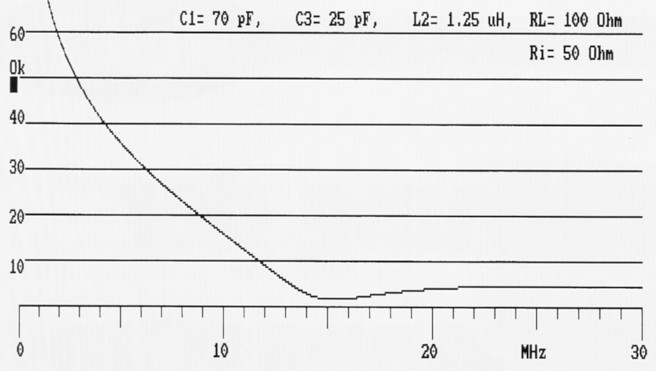
Bild 10: Dämpfung (HP) in (logarithmischen) dB nach der Vierpolmethode.
Bild 11 demonstriert endlich die numerische Dämpfung für ein L-C-L-Tiefpassfilter (TP) nach der Phasenmethode. Die linke Skala fur U1 / U2 hat den zweifachen Maßstab der bisherigen Skalen. Die Durchlassfrequenz ist 7 MHz. Die Dampfung der hohen Frequenzen liegt ab 8,5 MHz über 6 und ist damit recht ordentlich. Auch die tiefen Frequenzen werden ausreichend unterdrückt.
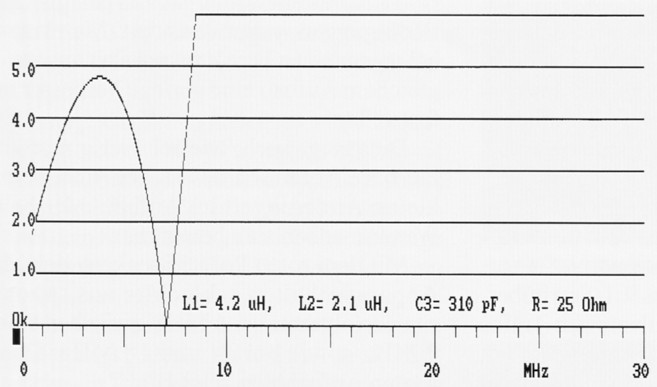
Bild 11: Numerische Dümpfung (TP) nach der Impedanzmethode.
Bild 12 zeigt ein L-C-L-Tiefpassfilter und den Durchlass nach der Phasenmethode. Die Durchlassfrequenz ist 21 MHz. Ab 26 MHz wird unwesentlich gedämpft. Bei den tiefen Frequenzen wird nur wenig gedämpft.
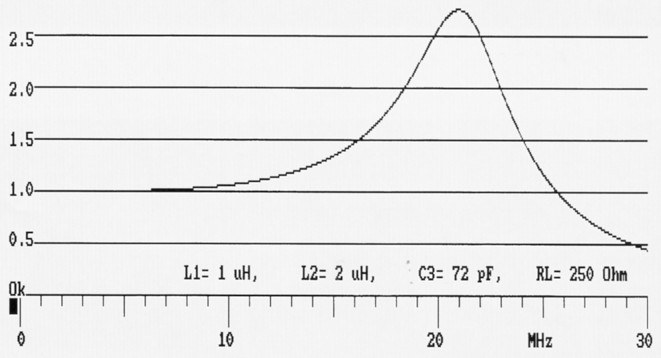
Bild 12: Numerischer Durchlass (TP) nach der Phasenmethode.
Bild 13 zeigt für das gleiche Filter die numerische Dämpfung U1 / U2. Eine wünschenswerte Dämpfung der Oberwellen findet erst ab ca. 26 MHz statt. Die unerfreuliche Dämpfung bei der Durchlassfrequenz von 21 MHz lässt sich durch bessere Einstellung des Filters beseitigen.
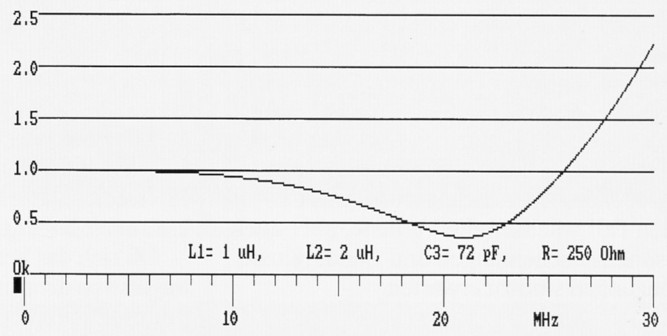
Bild 13: Numerische Dämpfung (TP) nach der Phasenmethode.
Zusammenfassung
Die Antennenkoppler in T-Schaltung konnen die Antennenimpedanz an die 50-Ω-Ausgangsimpedanz des Transceivers sehr gut anpassen und ein SWR von 1 im Kabel vom TRX zum Koppler bewirken. Die Hochpass-Schaltung (C-L-C) dämpft zwar die Frequenzen über der Arbeitsfrequenz aber nicht mehr als höchstens 10 dB. Die Dämpfung unterhalb der Arbeitsfrequenz ist gut. Die Tiefpass-Schaltung (L-C-L) dämpft Frequenzen unter der Arbeitsfrequenz um nicht mehr als etwa 10 dB. Die Dämpfung oberhalb der Arbeitsfrequenz ist gut. Hochpässe haben für Frequenzen oberhalb der Arbeitsfrequenz nur mäßge Dampfung. Tiefpasse dampfen unterhalb der Arbeitsfrequenz nur gering.
Für die Anregung zu dieser Arbeit und die zahlreichen Hinweise sei Herrn Professor Dr. Gerd Janzen, DF6SJ, herzlicher Dank gesagt.
Literatur und Quellen
- R. Feldtkeller, Einführung in die Vierpoltheorie der elektrischen Nachrichtentechnik, 6. Aufl., Stuttgart, 1953 Hirzel.
- Hütte, Des Ingenieurs Taschenbuch, Fernmeldetechnik, 28. Aufl., Berlin und Munchen, 1962 W. Ernst & Sohn, hier Seite 82.
Karl H. Hille, DL1VU.