Tangens en cotangens
Tangens en cotangens zijn goniometrische functies. De naam tangens komt van 'raaklijn' in het Latijn (tangens betekent rakend). Het argument van de tangens en de cotangens wordt vaak gezien als een hoek en dat heeft te maken met de oorspronkelijke definitie van deze functies. De tangens was gedefinieerd als de verhouding van de overstaande en de aanliggende rechthoekszijde in een rechthoekige driehoek. Deze oorspronkelijke definitie beperkte echter het domein van het argument van 0° tot 90° (behalve 90° zelf, waar de tangens niet gedefinieerd is). De inverse functie van de tangens is de arctangens of boogtangens, die voor een gegeven waarde van de tangens als functiewaarde de oorspronkelijke hoek (tussen -90°en +90°) geeft.
Raaklijn
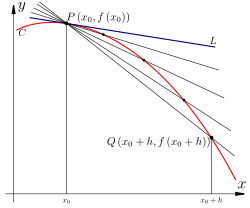
De raaklijn, tangens of tangent aan een kromme in een punt van de kromme is in de meetkunde de rechte lijn door dat punt met dezelfde richting als de kromme. Het punt waarin de raaklijn de kromme raakt heet raakpunt. De raaklijn is de benadering van de kromme in het raakpunt door een rechte lijn. De raaklijn kan de kromme eventueel nog snijden in een ander punt dan het raakpunt.
De raaklijn (L) in een punt P van de kromme kan gezien worden als het limietgeval van de lijn door P en een ander punt Q van de kromme als het punt Q het raakpunt P nadert. Daaruit ziet men ook dat niet in elk punt van een willekeurige kromme een raaklijn bestaat. De kromme zal aan bepaalde eisen van differentieerbaarheid moeten voldoen.
Goniometrische cirkel
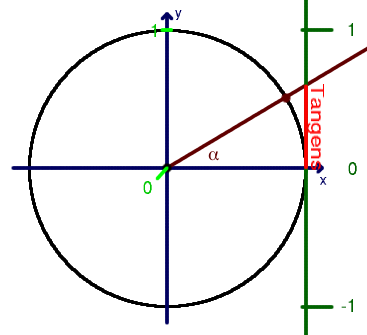
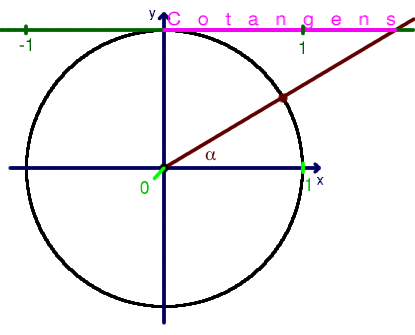
De functiewaarde van de tangens loopt van 0 tot 8, voor een argument lopend van 0° tot 90°, en van -8 terug naar 0 voor een argument lopend van 90° tot 180°; daarbuiten wordt de functie periodiek voortgezet. Daarnaast geldt dat tan( -α) = - tan(α).