Rob's web

Problemlösungen beim Bau von Senderverstärkern für KW-Bereiche 8

Home - Techniek - Electronica - Radiotechniek - Radio amateur bladen - CQ-DL - Problemlösungen beim Bau von Senderverstärkern für KW-Bereiche 8

---

Auf dem Wege zum Gitterbasis-Senderverstärker

Unter der Überschrift "Problemlösungen beim Bau von Senderverstärkern für KW-Bereiche" hat der Verfasser versucht, den Funkamateuren zu helfen, die sich daranmachen, einen Senderverstärker in Kathodenbasisschaltung zu entwerfen und selbst zu bauen.(11) Nun soll die Gitterbasisschaltung näher betrachtet werden.

Ein Vorteil der Kathodenbasisschaltung ist, daß die Senderöhre vergleichsweise wenig Steuerleistung benötigt.(2)(3)(4) So liefert z.B. die Tetrode QB 3/300 als Klasse-C-Verstärker bei U_an = 3000 V mehrals 350 W Ausgangsleistung, wenn weniger als 5 W Steuerleistung zugeführt werden.(4)

Als Nachteil empfinden es Funkamateure, daß Selbsterregungserscheinungen nur dann vollkommen ausgeschlossen sind, wenn Neutralisation angewendet wird. Der Verfasser hofft, daß es ihm gelungen ist, die interessierten Leser davon zu überzeugen, daß mit einfachen Mitteln eine leichteinstellbare, zuverlässige und vor allem frequenzunabhängige Neutralisation zu verwirklichen ist.

Einen geringeren Aufwand an Einzelteilen erfordern Senderverstärker, die in Gitterbasisschaltung aufgebaut sind. Sie bedürfen - zumindest im KW-Bereich - keiner Neutralisation, keiner Schirmgitterspannung und ggf. sogar keiner Steuergittervorspannung. Diese Vorteile werden mit dem Nachteil erkauft, daß Gitterbasis-Senderverstärker, deren Ausgangsleistung 750 W nicht übersteigt, um eine oder zwei Größenordnungen höhere Steuerleistungen benötigen als vergleichbare Kathodenbasis-Senderverstärker.

Steuersender, die 100...150 W Ausgangsleistung liefern, sind allemal geeignet, und daher ist auch eine Vielzahl der heutzutage industriell für Funkamateure gefertigten KW-Transceiver für die Aussteuerung von Gitterbasis-Senderverstärkern verwendbar.

Vergleichsweise nur wenige Funkamateure verfügen über die erforderlichen Kenntnisse von Theorie und zugleich auch Technologie zeitgemäßer KW-Transceiver, daß sie befähigt wären, solch komplizierte Funkgeräte selbst zu entwerfen und zu bauen.

Der Eingangswiderstand Re des Gitterbasis-Senderverstärkers und sich durch ihn ergebende Folgen

Charakteristisch für Gitterbasis-Senderverstärker ist vor allem ihr vergleichsweise kleiner Eingangswiderstand R_e, der zwischen Kathode und Masse wirksam ist. R_e ist röhrentypspezifisch und liegt im Bereich von nureinigen 10 Ω bis zu einigen 100 Ω. Weil Res° klein ist, bedarf ein Gitterbasis-Senderverstärker rechthoherSteuerleistung, von der allerdings bis zu 10 %das Steuergitter durchdringen und als Teil der Ausgangsleistung auftauchen.(17)

Die Hersteller von Senderöhren, die für Gitterbasis-Betrieb bestimmt oder für ihn auch brauchbar sind, sind offenbar bemüht, sie so zu gestalten, daß ihr Eingangswiderstand - ggf. auch erst nach Parallelschaltung zweier Röhren gleichen Typs mit übereinstimmenden (!) Kenndaten - bei 50 Ω liegt, also beim Wellenwiderstand vieler Koaxialkabeltypen und damit auch beim Ausgangswiderstand R₂ industriell gefertigter KW-Transceiver.

Es liegt dann verführerisch nahe, den KW-Transceiver-Ausgang über Koaxialkabel unmittelbar mit dem Gitterbasis-Senderverstärker-Eingang zu verbinden, weil dann formal mit R₂ = Z_L = R_e Anpassung vorliegt. Jedoch: Um eine verzerrungsfreie Verstärkung zu erzielen, die durch Messung der IntermodulationsprociLkte bestimmbar ist(19)(21)(22), ist ein Schwingkreis zwischen Steuersender und Senderverstärker erforderlich. In der für Funkamateure zugeschnittenen Fachliteratur wird auf das Collins-Filter hingewiesen(1)(21), mit einem Gütefaktor Q = 2 ... 3 berechnet. Keine Antwort allerdings findet man auf die unausweichliche Frage, wie z. B. ein Collins-Filter zu berechnen ist, das genau das tut, was man nicht von ihm erwartet, nämlich nichtzu transformieren, wenn z. B. R₁ = 50 Ω und auch R₂ = 50 Ω. In einer tabellarischen Zusammenstellung von Beträgen für C₁ C₂ und L, wenn R₁ = 50 Ω und R₂ = 20 ... 250Ω (21), findet man für den Fall R₁ = R₂ = 50 Ω die Beträge C₁ = C₂ = 227 pF und L = 0,57 µH, wenn der Kathoden-Schwingkreis eines Gitterbasis-Senderverstärkers für das 20-m-Band bestimmt ist. Die Resonanzfrequenz eines mitd iesen Komponenten aufgebauten Schwingkreises beträgt

Das Ergebnis macht stutzig und läßt den Leser den Verdacht schöpfen, daß nicht Formeln für die Berechnung von Collins-Filtern verwendet wurden - genauer: gar nicht verwendet werden konnten -, sondern Formeln, mit deren Hilfe sogenannte passive Vierpole berechnet werden, die den Gütefaktor Q beiseite lassen und schon darum nur ferne Verwandte der Formeln für CollinsFiltersind. DerVerdachtwirddurch Hinweise in einigen Beiträgen erhärtet, in denen die Verfasser mitteilen, daß Q =1 gesetzt wurde.(21)

Im Rahmen weitverzweigter, zu einem Konvolut angewachsener Korrespondenz, die sich auf den vorliegenden Beitrag bezieht, hat der Verfasser herausbekommen, daß der industrielle KW-Großsenderbau passive Vierpole in der Form von π-Filtern in Gitterbasis-Senderverstärkern als Kathoden-Schwingkreise anwendet. Offenbar also reicht der Gütefaktor Q = 1 eines Kathoden-Schwingkreises aus sicherzustellen, daß z.B. eine Sinusschwingung unverzerrt ein π-Filter passiert.(21)

Das π-Filter als passiver Übertragungsvierpol zwischen Steuersender und Gitterbasis-Senderverstärker

Das Schaltschema eines sogenannten passiven Vierpols, der π-Filter genannt wird, weil im Längsweg ein Widerstand liegt, der von zwei Widerständen flankiert wird, die sich in Querwegen befinden, deckt sich im Prinzip mitdem eines Collins-Filters (Bild 1).

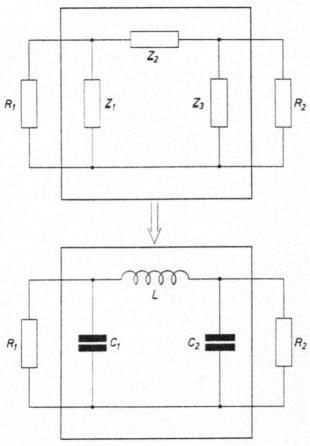
Bild 1: Prinzipieller Schaltplan eines Vierpol-Tiefpasses mit seinen drei Impedanzen Z₁ Z₂ und Z₃ in π-Anordnung, oben, und konkreter Schaltplan, unten, mit den berechenbaren Bauteilen. Der Vierpol funktioniert wie ein Transformator und paßt den Ausgangswiderstand R₁ eines Steuersenders an den Eingangswiderstand R₂ eines Gitterbasis-Senderverstärkers an.

Z₁ Z₂ und Z₃ sind Impedanzen, komplexe Widerstände, die, entsprechend der Formel Z = R + jX, sowohl Wirkwiderstand, als auch Blindwiderstand besitzen.

Die drei Impedanzen bilden den passiven Vierpol, der wie ein Transformator wirkt, und derso gestaltetsein soll, daß er ihm zugeführte Steuerleistung (Wirkleistung) ungeschwächt (ungedämpft) an seinen Ausgang überträgt: Der passive Vierpol befindet sich zwischen einem aktiven Zweipol (Steuersender und einem passiven Zweipol (Senderverstärker), zwischen einer Quelle und einem Verbraucher.(17) Der passive Vierpol wird eingangsseitig vom Ausgangswiderstand des Steuersenders, ausgangsseitig vom Eingangswiderstand des Senderverstärkers abgeschlossen, von R₁ bzw. R₂.

Das Symbol R besagt, daß im Rahmen der Berechnung eines passiven Vierpols die Abschlußwiderstände als Wirkwiderstände (rein "ohmsche" Widerstände ohne jX-Anteile) betrachtet werden.

R₁ entspricht immer dem Wellenwiderstand Z_L des Koaxialkabels, das Steuersender und Antenne beim Stehwellenverhältnis 1 : 1 verbinden würde, wenn der Steuersender als "Endstufe" verwendetwürde. Es wird daher im allgemeinen R₁ = 50 Ω gesetzt, wenn erwünscht, auch R₁ = 52 Ω oder 53 Ω, was Erhöhungen um 4 % bzw. 6 % entspricht.

Ob sich diese Genauigkeit für unsere Zwecke rechtfertigen läßt, möge der geneigte Leser - am Ende dieses Beitrags angelangt - selbst entscheiden.

R₂ ist der Eingangswiderstand der als Gitterbasisverstärker betriebenen Röhre. Auch er wird, idealisiert, als Wirkwiderstand in die Berechnungen einbezogen. Hier liegtes auf der Hand, daß R₂, z. B. die Eingangskapazität C_kg der Röhre einschließt; um ihren Betrag muß die Impedanz Z₃ beim Abgleich des fertiggestellten π-Filters verringert werden.

Der Eingangswiderstand Re in Gitterbasisschaltung betriebener Senderöhren

Selbstverständlich schaut man im entsprechenden Datenbuch für Senderöhren nach, ob man für einen bestimmten Röhrentyp Angaben über seinen Eingangswiderstand bei Gitterbasisbetrieb findet. Im allgemeinen ist das für einen Röhrentyp spezifisch erstellte Datenblatt noch mehr ins einzelne gehend. Am ehesten wird man fündig, wenn ein Röhrentyp speziell für Gitterbasisbetrieb entwickelt worden ist(15)(16) oder wenn ein für diese Betriebsart geeignet erscheinender Röhrentyp in einem für Messungen bestimmten Senderverstärker erprobt wurde.

Helfen Datenbücher oder -blätter nicht aus der Klemme, muß man sich auf Formeln stützen, mit deren Hilfe R_e berechenbar ist.

Die Faustformel R_e ≈ 1/S führt zu zu kleinen Beträgen und ist selbst Funkamateuren nicht zumutbar: nomen est omen. Zu wirklichkeitsnahen Ergebnissen führen die Formeln

(23)

und

(25)

(In den Publikationen 23, 25 steht R_a statt R_A. Der Verfasser verwendet R_A, um Homogenität der Index-Anwendung zu gewährleisten: im ersten Abschnitt der vorliegenden Darstellung(11) wurde für "Arbeitswiderstand" das Symbol R_A benutzt.)

In die soeben vorgestellten Formeln ist die Steilheit S in A/V, nicht in mA/V, einzusetzen, R_A und R_i müssen in Ω berücksichtigt werden.

D ist der sogenannte Durchgriff, der nur sehr selten noch im Rahmen der Kenndaten für eine Röhre erwähnt wird; sie erwähnen aber den Verstärkungsfaktor µ, und dieser verhilft zu D, denn es ist

An die Stelle des "reinen"

muß jeweils das der Verstärkerklasse angepaßte treten(11), also für

Klasse-B-Betrieb

und für

Klasse-C-Betrieb

und es sei noch hinzugefügt für

Klasse-AB-Betrieb

So lautet denn z. B. die Formel für die Berechnung des Eingangswiderstandes bei Klasse-AB-Betrieb entsprechend 23

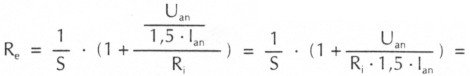
und entsprechend 25

R_i ist der statische Innenwiderstand der Röhre, und es ist

Im folgenden als Beispiel die Berechnung eines Eingangswiderstandes.

Gegeben sind S = 15mA/V, U_an = 3000V, I_an = 350mA, µ = 160.

Es ist

Die andere Formel ergibt

Die für das vorstehende Beispiel verwendeten festen Größen entstammen den Kenndaten zur Triode T 150-1, die der Hersteller offensichtlich auch im Hinblick auf Gitterbasis-Senderverstärker entwickelt hat, die den für uns gülti gen und bindenden gesetzlichen Vorschriften genügen.(15)(16)

Schon bei vergleichsweise flüchtiger Betrachtung der beiden zitierten Formeln für die Berechnung des Eingangswiderstandes R_e wird deutlich, daß R_e von den nicht-festen Größen U_an, I_an und dem "Klassenfaktor" 1,5 bzw. 1,6 bzw. 2 abhängt: R_e wächst mit wachsendem Quotienten und wird kleiner mit kleiner werdendem.

Das macht deutlich, wie wenig brauchbar die erwähnte Faustformel für R_e ist.

Ausführliche Kenndaten für Senderöhren unterscheiden zwischen statischer und dynamischer Kathodenimpedanz.(16) Mit den vorstehend angeführten Formeln wird die statische Kathodenimpedanz R_e berechnet.

Die Berechnung eines mit R₁ und R₂ abgeschlossenen π-Filters - ein höchst kompliziertes Unterfangen

Vorgegebenes R₁ und berechenbares R₂ verringern die Zahl der noch zu berechnenden Komponenten eines, wie man sagt, "beschalteten" passiven Vierpols von fünf auf drei. Allzuleicht verfällt man der Vorstellung, daß es dann wohl möglich sein müsse, die komplexen Impedanzen Z₁, Z₂ und Z₃ (Bild 1) sozusagen mühelos zu berechnen.

Es ist aber nicht möglich, in elementarer Weise mit nur zwei gegebenen Beträgen - R₁ und R₂ - drei andere, mit diesen funktional verknüpfte, numerisch unmittelbar zu berechnen. Das ist nur mit Hilfe von Zusatzbedingungen möglich, die sehr verwickelt sind.(24)(28)

Ermittlung der Blindwiderstände eines π-Filters, das als transformierender Kathoden-Schwingkreis verwendet werden soll, mit Hilfe zweier Ortskurven

In geradezu klassischer Weise, mit Lineal und Zirkel, wie schon angedeutet, ist die Aufgabe zu lösen, und daß man zur Vereinfachung Millimeterpapier benutzt, macht das Adjektiv "klassisch" nicht unangemessen.

Zeichnerische Grundlage ist die sogenannte Gaußsche Zahlenebene (Bild 2). Abszissenachse (x-Achse) und Ordinatenachse (y-Achse) stehen senkrecht aufeinander und treffen sich im Nullpunkt 0; die waagerechte Achse heißt reelle Achse, und auf ihr werden Wirkwiderstände R abgetragen; die senkrechte Achse wird imaginäre Achse geben mit wissenschaftlichen Taschenrechnern und hochgezüchteten Cornputern gemäß ist.

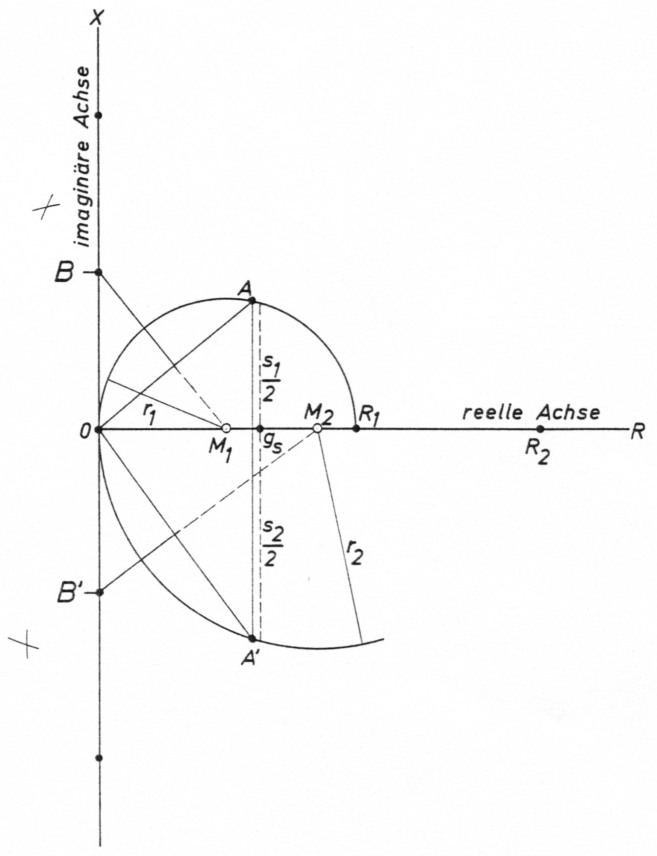
Bild 2: Ermittlungder Impedanzen Z₁, Z₂ und Z₃ (s. Bild 1) mit Hilfe einer Ortskurven-methode. Gaußsche Zahlenebene mit reeller und imaginärer Achse. Die Scheitel zweier Halbkreise münden im Nullpunkt 0; der obere Halbkreis hat den Halbmesser R₁/2, der untere den Halbmesser R₂/2. Das Dreieck A0A' führt zu den gesuchten Impedanzen eines π-Filters, das - in diesem Fall - von R₁ = 50 Ω auf R₂ = 85 Ω transformiert. 8,7 mm entsprechen 1 cm.

Befreiung aus der Zwangslage mit Lineal und Zirkel

Im Vergleich zu dem, was im vorigen Absatz angedeutet wurde, sind grafische Verfahren, Vierpole zu entwickeln, erheblich leichter zu beherrschen. Zwei Verfahren stehen zur Verfügung: Anwendung des Smith-Kreisdiagramms oder einer Ortskurvenmethode.

Will man nach Smith vorgehen, ist man gezwungen, mit Smith-Doppeldiagrammen zu arbeiten, da man sich mit Wirkwiderständen R und mit Wirkleitwerten Y gleichzeitig beschäftigen muß.(18) Obendrein sind gedruckte Smith-Doppeldiagramme leider im Handel nicht mehr erhältlich.

Beträchtlich einfacher ist es, mit Hilfe von sogenannten Ortskurven Z₁, Z₂ und Z₃ zu bestimmen.(17)(25) Numerisch führt dieses Verfahren gleich zu Beginn zu genaueren Zahlenfolgen als das nach Smith, was aber nicht entscheidend ist, da Stellen nach dem Komma in bezug auf das angestrebte Ziel praktisch vernachlässigbarsind und daherdurch Auf-oder Abrunden beseitigt werden dürfen. Im vorhinein nicht erfaßbare Faktoren spielen eine untergeordnete Rolle, die erst beim Abgleich des Vierpols erfaßbar und ggf. zu beseitigen sind: Es ist z. B. von höchst untergeordneter Bedeutung, ob man für einen Blindwiderstand den Betrag 85 Ω oder 83 Ω oder 88 Ω erhält. Ohnehin kann man dem rein grafischen Ortskurvenverfahren ein es rechnerisch nachvollziehendes an die Seite stellen, was sicherlich dem gegenwärtigen Le-.......... nannt, denn auf ihr werden Blindwiderstände X ermittelt. Beide Achsen werden, vom Nullpunkt ausgehend, in gleichem Maßstab lineargeteilt(auf Millimeterpapier gängiger Art- s. Bild 2 - ist das ohnehin der Fall).

Die Ortskurvenkonstruktion wird wie im folgenden beschrieben vollzogen (Bild 2). Um den Mittelpunkt M₁ auf der reellen Achse, der R₁/2 vom Nullpunkt 0 entfernt ist, wird ein Halbkreis mit dem Halbmesser R₁/2 = r₁ gezeichnet; er beginnt bzw. endet im Nullpunkt 0 und verläuft oberhalb der reellen Achse.

Um den Mittelpunkt M₂ auf der reellen Achse, der R₂/2 vom Nullpunkt 0 entfernt ist, wird ein Halbkreis mit dem Halbmesser R₂/2 gezeichnet; auch er beginnt bzw. endet im Nullpunkt 0, verläuft aber unterhalb der reellen Achse. Die Lage des Punktes g_s auf der reellen Achse wird mit der Formel

bestimmt.

Parallel zur imaginären Achse wird durch den Punkt g_s eine Strecke gezeichnet, die von Halbkreisperipherie zu Halbkreisperipherie reicht (in Bild 2 gestrichelt). Diese Strecke setzt sich aus den Halbsehnen s₁/2 und s₂/2 zusammen.

s₁/2 + s₂/2 sei s_max, denn s₁/2 + s₂/2 ist die längste Halbsehnen-Gesamtstrecke zwischen den beiden Halbkreisperipherien. Sie läßt sich wie folgt berechnen:

Da s_max parallel zur imaginären Achse der Gaußschen Zahlenebene verläuft, ist s_max gleichfalls eine imaginäre Achse.

Der Betrag von s_max entspricht in bezug auf R₁ und R₂ dem induktiven Blindwiderstand X_{L max} eines π-Filters (s. auch Bild 1 und dort Z₂ und L).

In dem von den beiden Ortskurven umschriebenen Bereich von s_max bis zum Nullpunkt 0 (wo s = 0) entsprechen s₁/2 + s₂/2-Strecken induktiven Blindwiderständen X_L für π-Filter.

Um zu den Beträgen der Blindwiderstände X_c1 und X_c2 zu gelangen, werden die Endpunkte einer s₁/2 + s₂/2-Strecke mit dem Nullpunkt 0 verbunden. In Bild 2 sind die Strecken A0 und A'0 das Ergebn is dieser Schritte. Die beiden kürzeren Seiten des entstandenen Dreiecks sind mit dem Nullpunkt 0 verbundene Sehnen der Halbkreise. Auf jeder Sehne wird das Mittellot errichtet, das durch den jeweils zugehörigen Kreismittelpunkt verläuft; man muß also jeweils nur amf einer Seite mit zwei Zirkelschlägen den Punkt ermitteln, der mit M₁ bzw. M₂ zu verbinden ist. Wo diese Geraden die imaginäre Achse schneiden, findet man die Beträge für X_c1/2 und X_c2/2, oberhalb und unterhalb des Nullpunktes 0 (Die Schnittpunkte befinden sich bei B und B').

Bild 2 kann man entnehmen: R₁ = 50 mm ≡ 50 Ω, R₂ = 85 mm ≡ 85 Ω; AA' ≡ X_L ≈ 65mm ≡ 65 Ω; 0B ≡ X_c1/2 = 30mm und X_c2 = 2 × 30 Ω = 60 Ω; 0B' ≡ X_c1/2 ≈ 32 mm und X_c2 = 2 × 32 Ω = 64 Ω.

So einfach ist das.

Feinheiten des grafischen Berechnungsverfahrens leichter erkennbar zu machen, ist Aufgabe von Bild 3. Drei Dreiecke sind in dieser Darstellung zu sehen, deren Seiten durch unterschiedliche Linien leichter erkennbar gemacht sind: Strichlinien, Vollinien und Strichpunktlinien.

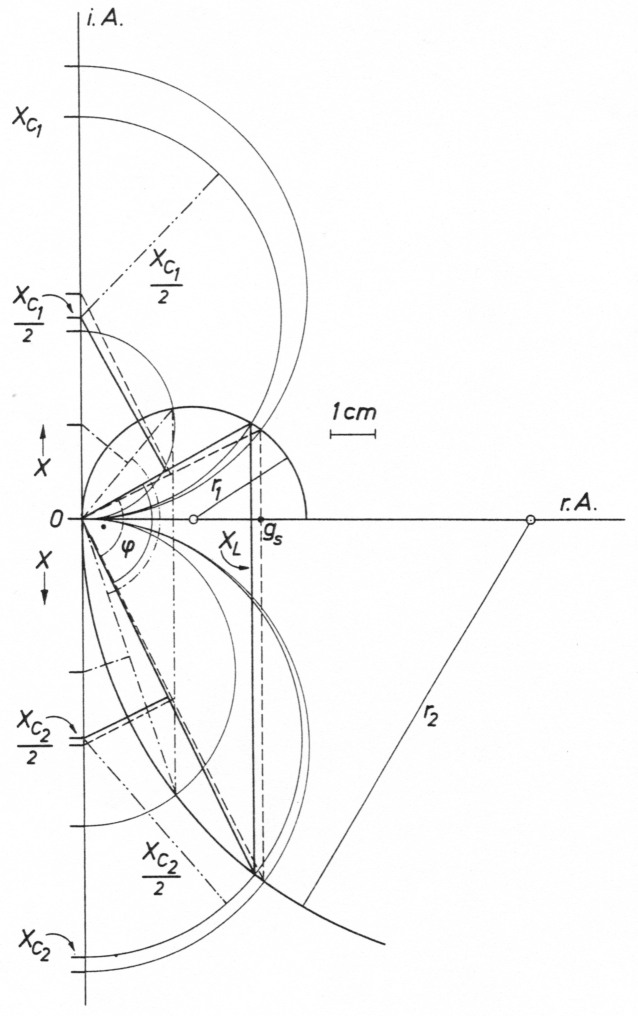
Bild 3: Ins einzelne gehende Darstellung der Ermittlung von π-Filter-Impedanzen mit Hilfe zweier Ortskurven. Dargestellt und durch unterschiedliche Linientypen verdeutlicht sind drei Ansätze, vom Fall φ = 900 bis zum Fall φ = 121°. Der dazwischen liegende Fall φ = 93° ist durch Beschriftung, die sich auf Impedanzen bezieht, hervorgehoben. Es handelt sich um Transformationen von R₁ = 50 Ω auf R₂ = 200 Ω (s. Maßstrich f. 1 cm).

Das Strichliniendreieck ist rechtwinklig, seine Hypotenuse geht durch den Punkt g_s und der rechte Winkel sitzt dem Nullpunkt 0 auf.

Wie auch immer die Beträge von R₁ und R₂ sein mögen, - wenn s_max als Hypotenuse verwendet wird, entsteht ein rechtwinkliges Dreieck (Bild 4).

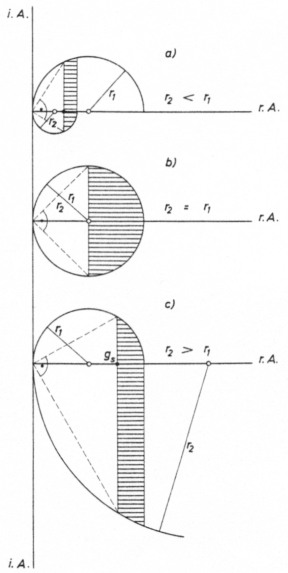
Bild 4: Die im Rahmen dieses Beitrages verwendete Ortskurvenmethode ist auch anwendbar, wenn der Eingangswiderstand R_e eines Gitterbasis-Senderverstärkers gleich oder kleiner als 50 Ω ist. Die Abbildung zeigt alle drei Möglichkeiten, und alle sind dem Grenzfall = 90° zugeordnet. In den schraffierten Bereichen sind π-Filter ungeeignet. (i. A. ist die imaginäre, r.A. die reelle Achse der Gaußschen Zahlenebene).

In dem Maße, in dem durch Parallelversch iebung von der smax-Hypotenuse weg Dreiecke mit immer kürzer werdender längster Seite (Hypotenuse) entstehen, wächst der Winkel φ des jeweiligen Dreiecks am Nullpunkt O. Der Winkel φ durchläuft dabei den Winkelbereich 90°... 180°, mit s = 0 bei 180°.

Ist der Punkt g auf der reellen Achse bekannt, durch den eine Hypotenuse s verläuft, kann der Winkel φ berechnet werden. Es ist

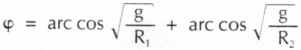
Beispiel: R₁ = 50 Ω, R₂ = 85 Ω, g = g₂ ≈ 31,5, φ = 37,5° + 52,5° = 90°; (Bild 2)

Beispiel: R₁ = 50 Ω, R₂ = 200 Ω, g = 20,5, φ = 50,2° + 71,3° = 121,5°; (Bild 3, Dreieck mit Strichpunktlinien-Seiten)

Es kann durchaus sein, daß man es mit Eingangswiderständen R_e zu tun bekommt, die kleiner als 50 Ω sind, daß also das π-Filter nicht aufwärts, sondern abwärts transformieren muß. Auch für solche Fälle ist die beschriebene Ortskurvenmethode gültig; daß der Fall R₁ = R₂ erfaßt wird, ist selbstverständlich (Bilder 2, 3 und 4).

Je größer der Winkel φ wird - fachsprachlich nennt man ihn "Phase φ" - und zugleich X_L kleiner, desto mehr nähern sich X_c1 und X_c2 dem Nullpunkt 0, d. h. desto kleiner werden auch diese Blindwiderstände, um so größer also die Kapazitäten, die sie darstellen.

Grundsätzlich gibt es für jede erdenkliche R₁-R₂-Paarung unendlich viele π-Filter-Kombinationen. Im Fall X_L = s_max und damit C₁ = C₂ sind die Kapazitäten am kleinsten.

Ein verblüffendes Zwischenergebnis

Spätestens an dieser Stelle taucht die Frage auf, ob es ein Merkmal gibt, das einen in die Lage versetzt zu entscheiden, welche der zahllosen C₁-C₂-L-Kombinationen die optimale ist.

Die Antwort auf diese Frage leuchtet umfassend ein, wenn an dieser Stelle darauf hingewiesen wird, daß es sich bei den π-Filtern, mit denen wir uns hier beschäftigen, um sogenannte Tiefpässe handelt, d.h. um Siebschaltungen, die Frequenzen bis zu einer berechenbaren hohen Frequenz passieren lassen, jenseits derselben aber noch höhere Frequenzen mehr und mehr dämpfen.

Der Übergang vom Durchlaß- zum Sperrbereich eines Tiefpasses der hier beschriebenen Art ist mathematisch mit einer hyperbolischen Konsinuskurve darstellbar (Bild 5). Ein idealer Tiefpaß würde den Sperrbereich SB nicht längs einer solchen Kurve zum Durchlaßbereich DB hin begrenzen, sondern längs einer senkrechten Geraden T, die parallel zur y-Achse verläuft.

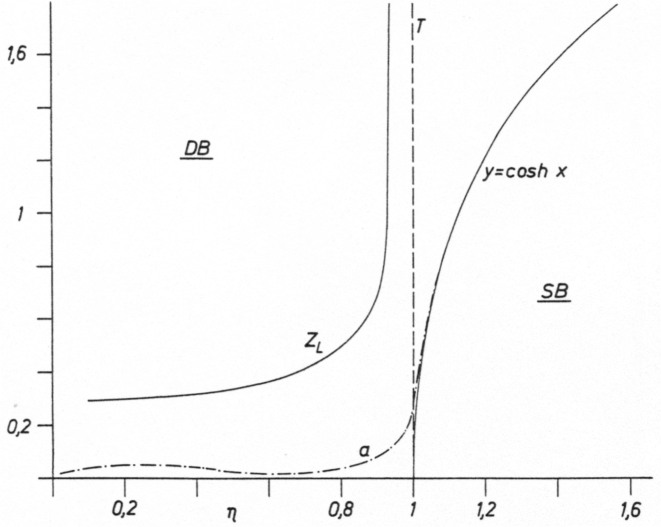
Bild 5: Schematisierte Darstellung des Verlaufs (1) der durch Verluste in Filter-Bauteilen verursachten Betriebsdämpfung a, die ins elementare Filter eingespeiste Steuerleistung schwächt, (2) des Wellenwiderstandes Z_L des Filters, der a beeinflußt, (3) der Grenze zwischen Durchlaßbereich DB und Sperrbereich SB, die einer hyperbolischen Kosinuskurve folgt, nicht aber dem idealen Verlauf entlang der Vertikalen T

Was eingangs dieses Beitrages schon als scheinbarer Widerspruch kurz erwähnt wurde, muß an dieser Stelle nochmals dargestellt werden.

Wenn man mit den Beträgen für X_c1, X_c2 und X_L für einen π-Filter-Tiefpaß, die mit Hilfe der dargestellten Ortskurvenmethode ermittelt wurden, C₁, C₂ und L für eine vorgegebene Amateurfunkbandfrequenz berechnet und dann die Resonanzfrequenz des mit eben diesen Komponenten aufgebauten Schwingkreises rechnerisch bestimmt, ist man mehr als verblüfft zu erfahren, daß die Resonanzfrequenz nicht mit der für die Umrechnungen X_c1 → C₁ usw. verwendeten Frequenz übereinstimmt!

Bedient man sich z. B. der Ergebnisse, die Bild 3 für das Vollinien-Dreieck liefert, erhält man X_c1 ≈ 89 Ω, X_c2 ≈ 97 Ω und X_L =100 Ω. Die vorgegebene Amateurfunkbandfrequenz sei f = 14 MHz. Dann ist C₁ ≈ 128 pF, C₂ ≈ 117 pF, L ≈ 1,14 µH. Die Reihenschaltung von C₁ und C₂ ergibt

und die Resonanzfrequenz beträgt

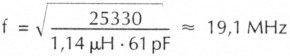
Im Rahmen von π-Filter-Tiefpaß-Berechnungen wird eine so ermittelte Resonanzfrequenz als Grenzfrequenz f_g bezeichnet.

Das verblüffende Ergebnis, daß ein in bezug auf die erforderlichen Blindwiderstände zum Erreichen eines vorgegebenen Transformationsverhältnisses einwandfrei berechnetes π-Filter mit den für eine vorgegebene Arbeitsfrequenz aus eben diesen Blindwiderständen ermittelten Beträgen für C₁, C₂ und L gar nicht auf eben dieser Arbeitsfrequenz Resonanz ergeben kann, führt zu einem wichtigen Faktor.

In der Fachliteratur wird dieser Faktor vorzugsweise am symmetrischen π-Filterabgeleitet, wenn also X_c1 = X_c2 = X_L und damit φ = 90 °.

Es sei X_c1 = X_c2 = X_L = 100 Ω (Bild 3, Dreieck mit gestrichelten Seiten). Die Arbeitsfrequenz sei f =14 MHz, und man erhält dann C₁ = C₂ ≈ 114 pF und L ≈ 1,14 µH.

Ein symmetrisches π-Filter ist stets aus zwei gleichen, sogenannten Halbgliedern zusammengesetzt, die im vorliegenden Fall jeweils 114 pF und 1,14 µH / 2 = 0,57 µH einschließen.

Die Grenzfrequenz eines Halbgliedes 25 beträgt

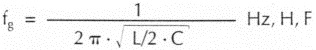
und im vorliegenden Fall also

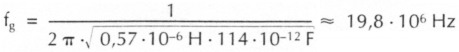
Das identische andere Halbglied des π-Filters hat zwingend die gleiche Grenzfrequenz f_g = 19,8 MHz und damit auch das ganze π-Filter.

Es leuchtet daher ein, daß man auch so die Grenzfrequenz f_g ermitteln kann(27):

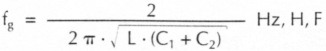
Es ist

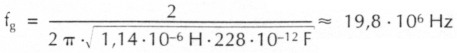
Bringt man den Faktor 2 π auf die linke Seite, so hat man es dort mit 2 × π × f_g zu tun, mit der Kreisgrenzfrequenz ω_g.

Mit der Arbeitsfrequenz f_A, auf der ein π-Filter-Tiefpaß betrieben wird, wird der Quotient

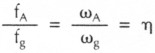
"normierte Frequenz" 25 bzw. "normierte Kreisfrequenz" genannt. Für das vorliegende Beispiel ist

Auf die große Bedeutung von η wird später genauer eingegangen.

Literatur

1. Anonymus: The ARRL Handbook for Radio Amateurs, 69. Auflage. ARRL, Newington CT 06111 USA 1992
2. Anonymus: Senderöhren. Brown Boveri, Baden (Schweiz) 1971
3. Anonymus: Senderöhren für Industriegeneratoren; Valvo. Hüthig, Heidelberg 1983
4. Anonymus: Senderöhren für Nachrichtensender; Valvo. Hüthig, Heidelberg 1985
5. Anonymus: Telefunken Laborbuch, Band I, Telefunken, Ulm 1957
6. Czichos, H. (Hrsg.): Hütte. Die Grundlagen der Ingenieurwissenschaften, 29. Auflage. Springer, Berlin 1991
7. Feldtkeller, R: Einführung in die Vierpol-theorie der elektrischen Nachrichtentechnik. Hirzel, Leipzig 1937
8. Fricke, H., Lamberts, K., Patzelt, E.: Grundlagen der elektrischen Nachrichtenübertragung. Teubner, Stuttgart 1979
9. Geschwinde, H.: Die Praxis der Kreis- und Leitungsdiagramme in der Hochfrequenztechnik. Franzis, München 1959
10. Kortz, M., Lentz, R.: Taschenbuch für Funkamateure und Techniker. Telekosmos, Stuttgart 1968
11. Lickfeld, K. G.: Problemlösungen beim Bau von Senderverstärkern für KW-Bereiche. CQ-DL 1-7, 1993
12. Lindner, H.: Elektro-Aufgaben, Band III. Fachbuchverlag, Leipzig 1991
13. Lindner, H., Brauer, H., Lehmann, C.: Taschenbuch der Elektrotechnik und Elektronik, 2. Auflage. Harri Deutsch, Thun und Frankfurt/Main 1986
14. Langer, K., Löcherer, K.-H. (Hrsg.): s. 1181
15. Mayr, H. P.: Röhren-Betriebsdaten für eine KW-SSB-PA am Beispiel der ABB-Triode T 150-1. CQ-DL 4, 1992
16. Mayr, H. P.: Die ABB-Triode T 150-1 im praktischen Einsatz. CQ-DL 6, 1992
17. Meinke, H., Gundlach, F. W.: Taschenbuch der Hochfrequenztechnik, 2. Auflage. Springer, Berlin 1962
18. Meinke, H., Gundlach, F. W.: Taschenbuch der Hochfrequenztechnik, 4. Auflage. Springer, Berlin 1986
19. Nährmann, D.: Das große Werkbuch Elektronik, 5. Auflage. Franzis, München 1989
20. Nührmann, D.: Meyer-Veit, T.: Mathematik für Elektroniker. Franzis, München 1989
21. Orr, W. I.: Radio Handbook, 23. Auflage, Howard W. Sams & Co., Indianapolis, IN 46268 USA
22. Pietsch, H.-J.: Kurzwellen-Amateurfunktechnik, 2. Auflage. Franzis, München 1984
23. Rose, G.: Große Elektronik-Formelsammlung, 18. Auflage. Franzis, München 1991
24. Rupprecht, W.: Netzwerksynthese. Springer, Berlin 1972
25. Schröder, H.: Elektrische Nachrichtentechnik, I. Band. Radio-Foto-Kinotechnik, Berlin 1959
26. Storer, J. E.: Passive Network Synthesis. McGraw-Hill, New York, 1957
27. Unger, H.-G.: Elektromagnetische Wellen auf Leitungen, 3. Auflage. Hiithig, Heidelberg 1991
28. Weißgerber, W.: Elektrotechnik für Ingenieure 3. Vieweg, Braunschweig/Wiesbaden 1991

Teil 1 - Teil 2 - Teil 3 - Teil 4 - Teil 5 - Teil 6 - Teil 7 - Teil 7a - Teil 8 - Teil 9

DL3FM, Prof. Dr. Karl Lickfeld.