Praktische filtertechniek 6; Butterworth-filters
| Orde n | Reële deel -α | Imaginaire deel +β |
|---|---|---|
| 2 | 0,70711 | 0,70711 |
| 3 | 0,5 | 0,86603 |
| 1 | ||
| 4 | 0,38268 | 0,92388 |
| 0,92388 | 0,38268 | |
| 5 | 0,30902 | 0,95106 |
| 0,80902 | 0,58779 | |
| 1 | ||
| 6 | 0,25882 | 0,96593 |
| 0,70711 | 0,70711 | |
| 0,96593 | 0,25882 | |
| 7 | 0,22252 | 0,97493 |
| 0,62349 | 0,78183 | |
| 0,90097 | 0,43388 | |
| 1 | ||
| 8 | 0,19509 | 0,98079 |
| 0,55557 | 0,83147 | |
| 0,83147 | 0,55557 | |
| 0,98079 | 0,19509 | |
| 9 | 0,17365 | 0,98481 |
| 0,5 | 0,86603 | |
| 0,76604 | 0,64279 | |
| 0,93969 | 0,34202 | |
| 1 | ||
| 10 | 0,15643 | 0,98769 |
| 0,45399 | 0,89101 | |
| 0,70711 | 0,70711 | |
| 0,89101 | 0,45399 | |
| 0,98769 | 0,15643 |
In dit deel beginnen we met de tabellen en karakteristieken voor de diverse filtertypen. Als eerste worden de Butterworth-tabellen en -karakteristieken gegeven, aangezien dit het meest bekende en waarschijnlijk ook meest gebruikte filtertype is.
Het Butterworth-filter wordt in de elektronica veel toegepast omdat het een vlak amplitudeverloop in het doorlaatgebied kombineert met een redelijk steile afval vanaf het kantel-punt. Als nadeel moet het niet-lineaire fasegedrag worden genoemd. De afval is vrij nauwkeurig 6-n dB per oktaaf, waarbij n de orde van het filter is. Het Butterworth-filter kan worden beschouwd als een soort kompromis tussen het Bessel-filter (slappe helling maar lineair fasegedrag) en het Chebyshev-filter (steile afval maar rimpel in de doorlaatband en slecht fasegedrag). Voor toepassingen waarbij een vlakke doorlaatkurve en een steile afval gewenst zijn, is het Butterworth-filter zonder meer de beste keuze.
In tabel 1 zijn de polen gegeven voor Butterworth-filters van de tweede tot de tiende orde. Aan de hand van deze data kan men met behulp van de in de vorige delen gegeven formules zelf filters berekenen.
De Butterworth-tabellen
Het dimensioneren gaat een stuk eenvoudiger met de hierna volgende tabellen, waarin de komponentenwaarden zijn vermeld voor passieve en aktieve filters van de tweede tot tiende orde. De waarden gelden altijd voor een filter met een kantelfrekwentie van 1 Hz. Tabel 2 geeft de komponentenwaarden voor een passief filter met gelijke bron- en uitgangsimpedantie. Voor de opzet die boven de tabel is getekend, gelden de koponenten-nummers die ook aan de bovenzijde van de tabel zijn aangegeven. Konstrueert men een filter zoals onder tabel 2 is getekend, dan geldt de komponentennummering die onder de tabel staat. Moeilijk is het niet, we zullen straks een duidelijk voorbeeld geven. Tabel 3 geeft de komponenten voor een passief filter met een verwaarloosbare bron-impedantie. In tabel 4 en 5 zijn de komponentenwaarden gegeven voor de aktieve filters met enkelvoudige tegenkoppeling. In tabel 4 wordt gewerkt met tweede- en derde-ordesekties. Wil men bijvoorbeeld een zevende-ordefilter ontwerpen, dan worden twee tweede-ordesekties en een derde-ordesektie achter elkaar geschakeld. Zoals we gezien hebben in deel 3, kan men ook uitsluitend tweedeorde-sekties toepassen en bij een oneven-orde-filter een passief RC-netwerk toevoegen. De gegevens hiervoor ziet u in tabel 5. We geven deze tabel ter illustratie om te laten zien dat het zo ook kan. In de meeste gevallen is de opzet uit tabel 4 praktischer. Bij de overige filtertypen zal tabel 5 dan ook niet meer gegeven worden.
 | ||||||||||
| Orde n | C1 | L1 | C2 | L2 | C3 | L3 | C4 | L4 | C5 | L5 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0,2251 | 0,2251 | ||||||||
| 3 | 0,1592 | 0,3183 | 0,1592 | |||||||
| 4 | 0,1218 | 0,2941 | 0,2941 | 0,1218 | ||||||
| 5 | 0,09836 | 0,2575 | 0,3183 | 0,2875 | 0,09836 | |||||
| 6 | 0,08238 | 0,2251 | 0,3075 | 0,3075 | 0,2251 | 0,08283 | ||||
| 7 | 0,07083 | 0,1985 | 0,2868 | 0,3183 | 0,2868 | 0,1985 | 0,07083 | |||
| 8 | 0,0621 | 0,1768 | 0,2647 | 0,3122 | 0,3122 | 0,2647 | 0,1768 | 0,0621 | ||
| 9 | 0,05527 | 0,1592 | 0,2438 | 0,2991 | 0,3183 | 0,2991 | 0,2438 | 0,1592 | 0,05527 | |
| 10 | 0,04979 | 0,1445 | 0,2251 | 0,2836 | 0,3144 | 0,3144 | 0,2836 | 0,2251 | 0,1445 | 0,04979 |
| L1 | C1 | L2 | C2 | L3 | C3 | L4 | C4 | L5 | C5 | |
 | ||||||||||
 | ||||||||||
| Orde n | C1 | L1 | C2 | L2 | C3 | L3 | C4 | L4 | C5 | L5 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0,2251 | 0,1126 | ||||||||
| 3 | 0,2387 | 0,2122 | 0,07985 | |||||||
| 4 | 0,2436 | 0,251 | 0,1732 | 0,06091 | ||||||
| 5 | 0,2459 | 0,2697 | 0,22 | 0,1423 | 0,04918 | |||||
| 6 | 0,2472 | 0,28 | 0,2472 | 0,1912 | 0,1206 | 0,04119 | ||||
| 7 | 0,2479 | 0,2836 | 0,264 | 0,2224 | 0,1679 | 0,1044 | 0,03541 | |||
| 8 | 0,2484 | 0,2904 | 0,2751 | 0,2432 | 0,2003 | 0,1491 | 0,09193 | 0,03105 | ||
| 9 | 0,2487 | 0,2932 | 0,2829 | 0,2579 | 0,2234 | 0,1816 | 0,1339 | 0,08204 | 0,02763 | |
| 10 | 0,249 | 0,2953 | 0,2884 | 0,2685 | 0,2414 | 0,2056 | 0,1656 | 0,1214 | 0,07407 | 0,02489 |
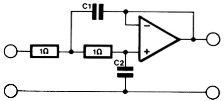 | 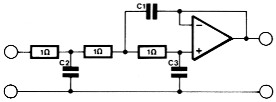 | ||||
| Orde n | C1 | C2 | C1 | C2 | C3 |
|---|---|---|---|---|---|
| 2 | 0,2251 | 0,1125 | |||
| 3 | 0,5644 | 0,2215 | 0,03221 | ||
| 4 | 0,4159 | 0,06091 | |||
| 0,1723 | 0,147 | ||||
| 5 | 0,515 | 0,04918 | |||
| 0,279 | 0,2155 | 0,06707 | |||
| 6 | 0,6149 | 0,04119 | |||
| 0,2251 | 0,1125 | ||||
| 0,1648 | 0,1537 | ||||
| 7 | 0,7152 | 0,03542 | |||
| 0,2553 | 0,09923 | ||||
| 0,2437 | 0,2126 | 0,07775 | |||
| 8 | 0,8158 | 0,03105 | |||
| 0,2865 | 0,08842 | ||||
| 0,1914 | 0,1323 | ||||
| 0,1623 | 0,1561 | ||||
| 9 | 0,9165 | 0,02764 | |||
| 0,3183 | 0,07958 | ||||
| 0,2078 | 0,1219 | ||||
| 0,2316 | 0,2112 | 0,08228 | |||
| 10 | 1,0174 | 0,0249 | |||
| 0,3506 | 0,07225 | ||||
| 0,2251 | 0,1125 | ||||
| 0,1786 | 0,1418 | ||||
| 0,1611 | 0,1572 | ||||
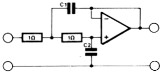 | 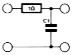 | ||
| Orde n | C1 | C2 | C1 |
|---|---|---|---|
| 2 | 0,2251 | 0,1125 | |
| 3 | 0,3183 | 0,07958 | |
| 0,1592 | |||
| 4 | 0,4159 | 0,06091 | |
| 0,1723 | 0,147 | ||
| 5 | 0,515 | 0,04918 | |
| 0,1967 | 0,1288 | ||
| 0,1592 | |||
| 6 | 0,6149 | 0,04119 | |
| 0,2251 | 0,1125 | ||
| 0,1648 | 0,1537 | ||
| 7 | 0,7152 | 0,03542 | |
| 0,2553 | 0,09923 | ||
| 0,1766 | 0,1434 | ||
| 0,1592 | |||
| 8 | 0,8158 | 0,03105 | |
| 0,2865 | 0,08842 | ||
| 0,1914 | 0,1323 | ||
| 0,1623 | 0,1561 | ||
| 9 | 0,9165 | 0,02764 | |
| 0,3183 | 0,07958 | ||
| 0,2078 | 0,1219 | ||
| 0,1694 | 0,1496 | ||
| 0,1592 | |||
| 10 | 1,0174 | 0,0249 | |
| 0,3506 | 0,07225 | ||
| 0,2251 | 0,1125 | ||
| 0,1786 | 0,1418 | ||
| 0,1611 | 0,1 | ||
De Butterworth-karakteristieken
Ten opzichte van de in deel 2 afgebeelde voorbeeld-karakteristieken zijn bij de definitieve karakteristieken enige dingen gewijzigd omwille van de duidelijkheid. Voor elk type filter worden drie series karakteristieken gegeven, waarin het volgende te zien is: De frekwentiekarakteristiek (figuur 1), de tijdvertraging (figuur 2) en het stapspanningsgedrag (figuur 3). De fasekarakteristiek is weggelaten omdat deze bij gebruik van een logaritmische schaal weinig informatie geeft over het al of niet faselineair zijn van een filter; figuur 2 vervult deze taak veel beter (een faselineair gedrag is hierin te herkennen aan een konstante tijdvertraging bij alle frekwenties). In elke figuur is de karakteristiek getekend van een tweede-, vierde-, zesde-, achtste- en tiendeorde-filter. Voor een oneven-orde-filter kan een tussenwaarde worden genomen. Op deze wijze blijft het aantal karakteristieken per figuur beperkt tot 5 en is alles nog goed te volgen.
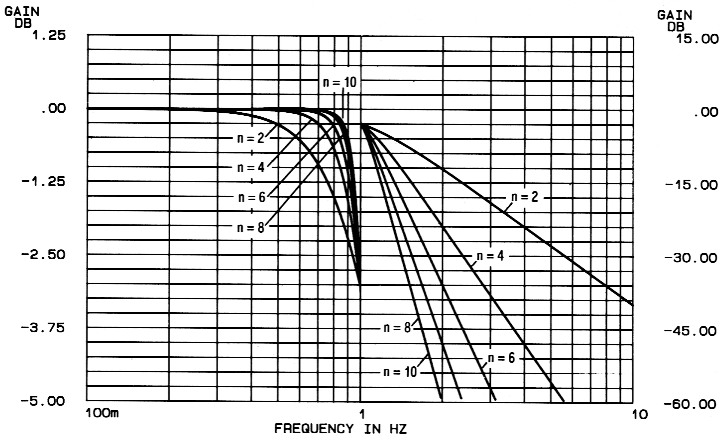
Figuur 1. De frekwentiekarakteristieken voor Butterworth-filters.
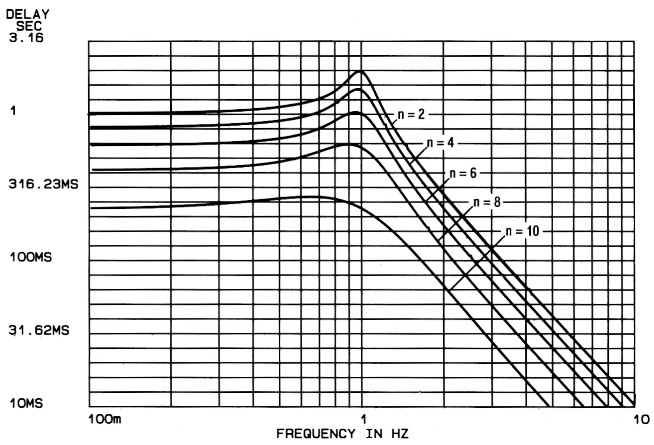
Figuur 2. De bijbehorende tijd vertragingskurves.
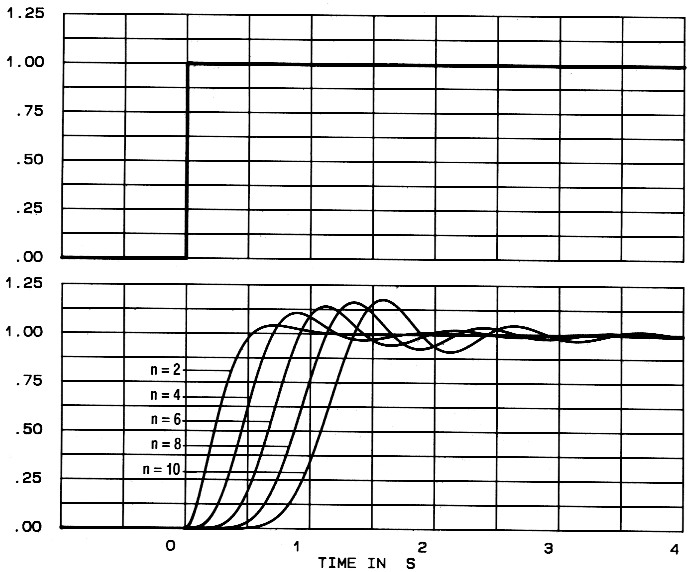
Figuur 3. De responsie op een stapspanning.
Bij figuur 1 moet nog even de opzet van de karakteristiek verklaard worden. Om het gedrag van het filter vlak voor het kantelpunt goed te kunnen weergeven, is voor het rechter gedeelte van de kurves (links van 1 Hz) een uitgerekte schaal genomen (die links naast de karakteristiek staat). Voor het gedeelte rechts van 1 Hz geldt een grovere schaal (rechts naast de karakteristiek). Het ziet er misschien een beetje vreemd uit, maar in het gebruik is deze opzet heel handig.
Twee voorbeelden
Bij elk filtertype dat we voorstellen, zullen ook enkele uitgewerkte voorbeelden worden gegeven, zodat men leert hoe de tabellen en kurves gebruikt moeten worden. Hier de eerste twee:
Voorbeeld 1
Ontwerp een passief Butterworth-laagdoorlaatfilter met een kantelpunt op 1600 kHz, voor een bron- en afsluitimpedantie van 50 Ω. Bij 3200 kHz moet de verzwakking minstens 20 dB bedragen.
Om er achter te komen hoe groot de verzwakking moet zijn bij welke frekwentie ten opzichte van de genormaliseerde frekwentie van 1 Hz, delen we eerst de twee frekwenties op elkaar:
3200 / 1600 = 2
In figuur 1 kijken we welke kurve bij f = 2 Hz minstens 20 dB verzwakking geeft. We komen dan terecht bij een vierde-orde-filter (een derde-orde-filter is te slap, dat geeft slechts 3.6 = 18 dB verzwakking per oktaaf). Voor het genormaliseerde filter worden de vierde-orde-waarden afgelezen in tabel 2. Dat resulteert in het schema van figuur 4a. We zouden het filter ook kunnen opzetten zoals onder tabel 2 is getekend en dan ziet het schema er uit zoals figuur 4b laat zien. Bekijk dit even goed, want als u dit snapt is de opzet van tabel 2 voor eens en altijd duidelijk.
De komponentenwaarden moeten nu nog worden aangepast aan de toegepaste in- en uitgangsimpedantie en de kantelfrekwentie:
C' = C / (f × R)
L' = L × R / f
Dat resulteert dan in de komponentenwaarden van de filters rechts in figuur 4.
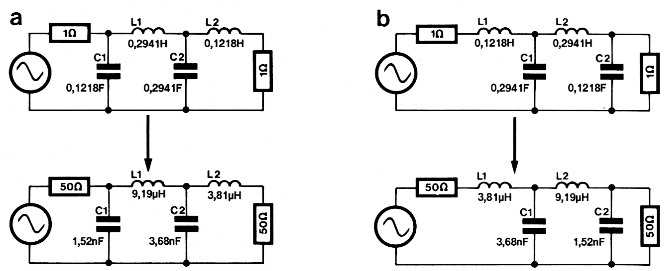
Figuur 4. Twee voorbeelden hoe een passief filter kan worden gedimensioneerd.
Enkele berekeningsvoorbeelden voor figuur 4a:
C1 = 0,1218 / (1600000 × 50) = 1,52 × 10-9 F = 1,52 nFL1 = 0,2941 × 50 / 1600000 = 9,19 × 10-6 H = 9,19 µH
Voorbeeld 2
Ontwerp een aktief vijfde-orde Butterworth-laagdoorlaatfilter met een kantel-punt op 5 kHz.
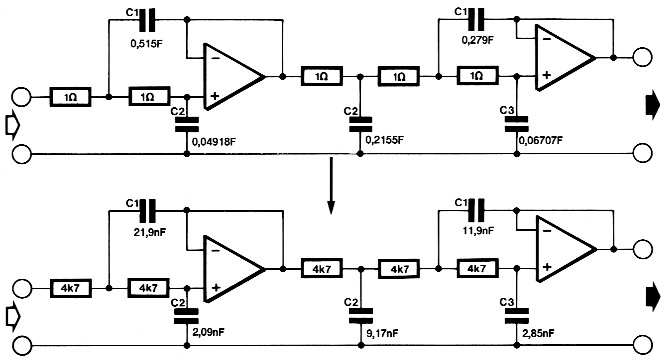
Figuur 5. De berekening van een aktief vijfde-ordefilter.
Dit is snel gemaakt. Het is een oneven-orde-filter, dus hebben we een tweedeorde-sektie nodig en een derde-orde-sektie, zoals boven tabel 4 is getekend. Deze twee sekties worden achter elkaar geschakeld en dan worden eerst de genormaliseerde komponentenwaarden uit de tabel ingevuld. Kies vervolgens een waarde voor de weerstanden, bijvoorbeeld 4,7 kΩ (dat is R in de formules). Bereken dan weer met de in het eerste voorbeeld gegeven formule (voor C') de "echte" komponentenwaarden.
Ook hier weer twee berekeningsvoorbeelden:
C1 = 0,515 / (5000 × 4700) = 21,9 × 10-9 = 21,9 nF
C2 = 0,04918 / (5000 × 4700) = 2,09 × 10-9 = 2,09 nF
Tot zover de Butterworth-filters. In deel 7 volgen de gegevens van de Bessel-filters.
Deel 1 - Deel 2 - Deel 3 - Deel 4 - Deel 5 - Deel 6 - Deel 7 - Deel 8 - Deel 9 - Deel 10