Praktische filtertechniek 10; Allpass filters
In het laatste deel van deze filter-kursus gaan we eens kijken naar netwerken die eigenlijk geen filters zijn maar toch onder de filters gerekend worden: de ailpass-netwerken. Dit zijn netwerken die een verandering van het faseverloop veroorzaken maar de amplitude van het ingangssignaal ongemoeid laten. Een apart soort filters waarmee heel nuttige dingen gedaan kunnen worden.
Eigenlijk zegt de naam "all-pass" al genoeg over de werking van dit soort netwerken: ze laten gewoon alles ongehinderd door. Helemaal klopt dat ook weer niet, want een allpass-netwerk doet wel degelijk iets met het ingangssignaal. Het signaal verlaat de allpassschakeling weer met een zekere faseverschuiving. Het is dus een soort vertragingsnetwerk. Zo'n schakeling kan gebruikt worden om een signaal in de tijd te vertragen of om het faseverloop van een bestaand filter te korrigeren.
Als we, zoals we ook bij de normale filters hebben gedaan, even in het komplexe vlak gaan kijken, dan zien we dat de nulpunten van een allpassfilter het spiegelbeeld van de polen zijn. Aangezien polen altijd links van de komplexe y-as liggen in verband met de benodigde stabiliteit van het netwerk, moeten de nulpunten dus altijd in de rechter helft liggen. Bij een eersteorde-netwerk hebben we in dat geval te maken met een reële pool-nulpuntkombinatie.
Het is nog aardig om te vermelden dat door het unieke karakter van een allpass-netwerk de optredende faseverschuiving altijd het dubbele bedraagt ten opzichte van een gewoon filter van dezelfde orde. Bij een eerste-orde filter bedraagt de maximale faseverschuiving 90°, terwijl dat bij een eerste-orde allpass-filter 180° is.
Eerste-orde netwerk
De overdrachtsfunktie van een eerste-orde allpassnetwerk is:
![]()
waarbij a de plaats van de pool aangeeft. De absolute waarde is:
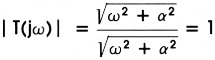
We zien dat bij elke frekwentie teller en noemer dezelfde waarde hebben. De hierbij behorende faseverschuiving bedraagt:
![]()
Aangezien bij allpassnetwerken ook de tijdvertraging (t) belangrijk is, kunnen we daar eveneens een berekening voor geven:
![]()
De tijdvertraging is bij een eerste-orde-netwerk altijd maximaal bij zeer lage frekwenties en neemt bij hogere frekwenties geleidelijk af. Het globale verloop wordt bepaald door de waarde van α. Bij kleine α-waarden is de tijdvertraging wel groot bij 0 Hz, maar deze neemt daarboven snel af. Bij grote α-waarden is de tijdvertraging weliswaar veel kleiner, maar ze blijft dan mooi konstant over een breder frekwentiebereik.
Tweede-orde netwerk
Bij een tweede-ordenetwerk zijn er wat meer vrijheidsgraden, waardoor de tijdvertragingskurve meestal beter aan de gestelde eisen kan beantwoorden. De overdrachtsfuntkie is hierbij:
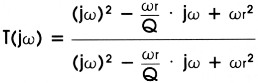
De absolute waarde van deze overdrachtsfunktie is weer een. Er is hier sprake van een resonantiekring, vandaar de aanwezigheid van de resonantiefrekwentie ωr. Deze frekwentie kan als volgt worden berekend:
![]()
α en β zijn hierbij de poolpunten van de gewenste funktie.
De Q-faktor is:
![]()
De faseverschuiving bij het tweede-orde netwerk bedraagt:
![]()
en de tijdvertraging kan worden berekend met de volgende formule:
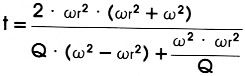
Zoals u ziet is het berekenen van een tweede-orde netwerk niet zo eenvoudig; in de praktijk ziet men dit ook niet vaak toegepast. De tijdvertraging is het grootst bij de resonantiefrekwentie. Bij een hogere Q-waarde wordt de piek in de tijdvertragingskurve ook groter.
Praktische passieve netwerken
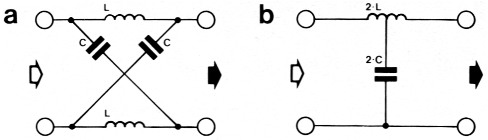
Figuur 1. Een eerste-orde vertragingsnetwerk: a. ladder-netwerk, b. asymmetrische opzet.
De opbouw van een eerste-orde vertragingsnetwerk is vrij eenvoudig. In figuur 1 is het schema gegeven van een ladder-netwerk en een ongebalanceerd netwerk. Beide filters hebben identieke in-en uitgangsimpedanties, zodat men direkt meerdere netwerken achter elkaar kan hangen. De berekening van zo'n netwerk is uiterst eenvoudig:
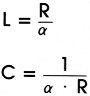
Hierbij is R de gewenste in-en uitgangsimpedantie. Het netwerk van figuur 1a zal verder bij de opbouw geen problemen geven. Bij de konfiguratie uit 1b moet men er aan denken dat hier gebruik wordt gemaakt van een spoel met een midden-aftakking, waarbij de magnetische koppelfaktor tussen de twee spoeldelen 1 moet zijn.
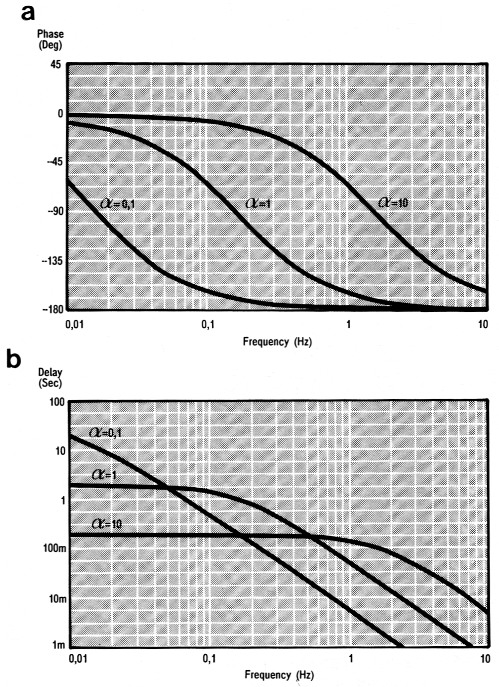
Figuur 2. De tijdvertraging van een eerste-orde netwerk bij een α van resp. 0,1, 1 en 10. Figuur a toont het faseverloop en b de tijdvertraging.
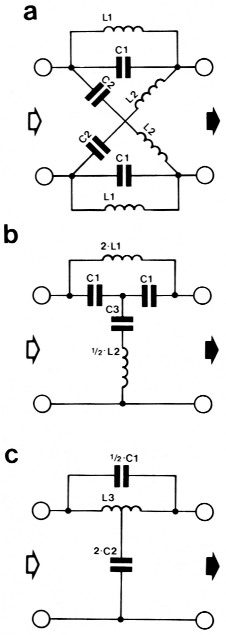
Figuur 3. Het schema van een tweede-orde ladder-netwerk (a), een ongebalanceerd netwerk voor een Q > 1 (b) en een Q < 1 (c).
In figuur 2 is de tijdvertraging weergegeven voor een α van 0,1, 1 en 10. Men ziet hier dat de waarde van a vrij gekozen kan worden, afhankelijk van de gewenste tijdvertragingskurve.
Het tweede-orde netwerk is wat ingewikkelder van opzet, waarbij men ook nog kan kiezen tussen een netwerk voor Q's groter dan 1 en Q's kleiner dan 1. Figuur 3 geeft achtereenvolgens een tweede-orde ladder-netwerk, een ongebalanceerd netwerk met "gewone" komponenten en een ongebalanceerd netwerk met een spoel met midden-aftakking. De eerste twee zijn bestemd voor een Q groter dan een en de laatste voor lagere Q-waarden. De waarden van de komponenten kunnen als volgt berekend worden:
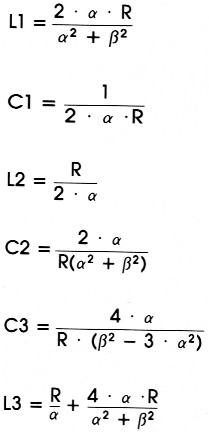
De faseverschuiving bij het tweede-orde netwerk bedraagt:
Aktieve schakelingen
Met aktieve schakelingen zijn de allpass-mogelijkheden nog wat groter dan bij de passieve netwerken, maar om het een beetje overzichtelijk te houden beperken we ons hier ook tot eerste- en tweede-ordeschakelingen.
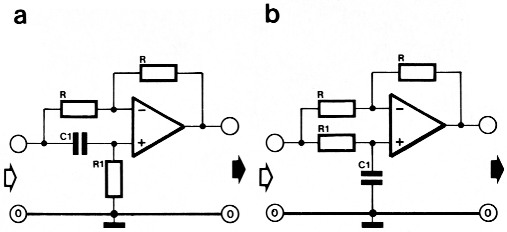
Figuur 4. De aktieve uitvoering van een eerste-orde netwerk. Figuur a toont een naijlend en figuur b een voorijlend netwerk.
Een aktieve eerste-ordesektie is te zien in figuur 4. Er zijn hier twee typen afgebeeld, een (4a) met een naijlende faseverschuiving en een (4b) met een voorijlende faseverschuiving. Daarnaast inverteren beide schakelingen het ingangssignaal ook nog eens (en dat heeft niets te maken met een faseverschuiving). Let er op dat deze twee schakelingen in veel toepassingen worden verwisseld. Men denkt dan dat de schakeling van 4b een naijlend karakter heeft, maar dat is pertinent fout. De berekening van zo'n eerste-orde netwerk is vrij eenvoudig, net zoals bij de passieve versie. Dat gaat zo:

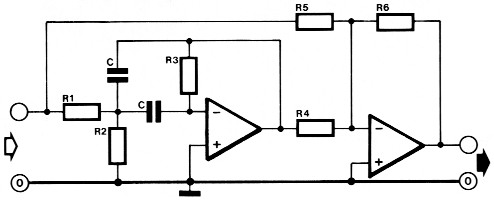
Figuur 5. Een aktief tweede-orde netwerk. Deze schakeling is geschikt voor een Q-waarde van 0 tot 20.
Bij het tweede-orde netwerk (figuur 5) bestaat de eenvoudigste aktieve schakeling uit een bandfilter en een sommator. De berekening kost hierbij wat meer moeite. Eerst kiezen we een geschikte waarde voor C en dan volgt de rest:
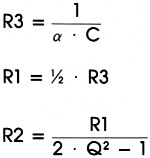
Ook voor R5 wordt een passende waarde gekozen (bijv. 22 k).
R6 = R5 (of groter, indien versterking gewenst is)
R4 = ½ × R5 (voor Q > 0,7)
Voor Q > 0,7 geldt:
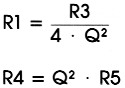
Het is mogelijk om met behulp van tweede-orde vertragingsschakelingen delay-lines te maken die een konstante tijdvertraging bezitten over een bepaalde frekwentieband. De poolpunten kunnen gewoon uit de tabellen gehaald worden. In verband met de vrij moeilijke berekening hiervan wordt deze mogelijkheid hier alleen even genoemd maar niet verder uitgewerkt. Eigenlijk geldt hetzelfde voor alle andere vertragingslijnen. Meestal worden voor een bepaalde toepassing zo'n specifieke eisen gesteld dat het moeilijk is om een paar algemene voorbeelden te geven. We laten het dan ook bij de formules. Met dit tiende deel besluiten we onze reeks praktische filtertechniek. Natuurlijk konden er nog veel meer dingen in behandeld worden, maar een serie die een jaar lang loopt lijkt ons voldoende voor het verkrijgen van een globaal inzicht in het onderwerp filters. Voor de geïnteresseerde lezer zal deze serie misschien de aanzet geven om zich verder te verdiepen in dit fascinerende onderwerp.
Deel 1 - Deel 2 - Deel 3 - Deel 4 - Deel 5 - Deel 6 - Deel 7 - Deel 8 - Deel 9 - Deel 10