Rob's web

Home - Techniek - Electronica - Electronicabladen - Elektuur / Elektor - Praktische filtertechniek 9; Chebyshev-filters 2

Praktische filtertechniek 9; Chebyshev-filters 2

Nadat we vorige maand de Chebyshev-filters met een doorlaatrimpel van 0,1 dB hebben bekeken, volgen nu de Chebyshev-filters met 0,5 dB rimpel. Deze hebben een nog grotere demping in de sperband dan hun 0,7-dB-soortgenoten, maar daar staat een toch wel aanzienlijke slingering in de doorlaatband tegenover.

De algemene voor- en nadelen van de Chebyshevfilters hebben we al in het vorige deel vermeld, zodat we daar verder niet meer op in hoeven te gaan. We stappen dan ook direkt over naar de tabellen.

Tabel 1. Chebyshevpoolpunten voor 0,5 dB rimpel.

Orde n	Reële deel -α	Imaginaire deel ±β
2	0,502	0,7278
3	0,2654	0,8913
	0,5309
4	0,1594	0,9509
	0,3849	0,3939
5	0,1053	0,9788
	0,2756	0,6049
	0,3406
6	0,07437	0,9941
	0,2032	0,7278
	0,2776	0,2664
7	0,05522	1,0034
	0,1547	0,8047
	0,2236	0,4466
	0,2482
8	0,04257	1,0094
	0,1212	0,8557
	0,1814	0,5718
	0,214	0,2008
9	0,03379	1,0136
	0,09731	0,8913
	0,1491	0,6616
	0,1829	0,352
	0,1946
10	0,02747	1,0165
	0,07971	0,917
	0,1242	0,7278
	0,1564	0,4672
	0,1734	0,161

Chebyshev met 0,5 dB rimpel

Ook hier geven de vijf tabellen weer alle informatie voor het berekenen van diverse 0,5-dB-Chebyshev filters. Evenals bij het 0,1-dB-filter van vorige maand is het ook hier in tabel 2 zo dat het niet mogelijk is om een even-orde-filter te berekenen voor een gelijke in- en uitgangsimpedantie. Bij de rr-filters is in deze tabel een verhouding van 2:1 aangehouden en bij de T-filters is dat 0,5:1 (of 1:2, het ligt er maar aan welke weerstand als referentie wordt genomen). De filterkarakteristieken tonen zoals altijd weer het duidelijkst de specifieke eigenschappen van het 0,5-dB-Chebyshev-filter. De rimpel is in figuur 1 goed zicht baar, hoewel men moet bedenken dat de eerste helft van de schaal in vertikale richting flink is uitgerekt. Echt dramatisch is het hier dus niet, het wordt pas storend bij rimpels van meer dan 1 dB. De afval is flink steil, zo bedraagt de demping van een vierde-orde filter bij 2 × f_k circa 33 dB! Het is misschien aardig om bij figuur 1 te vermelden dat het aantal "slingers" (heuvels en dalen) overeen komt met de orde van het filter. Dat geeft u een beetje een idee van de opzet en werking van dit type filter (bij meer rimpel gaat het doorlaatgebied steeds meer op een aantal aaneengeschakelde banddoorlaatkurves lijken). De tijdvertragingskurves in figuur 2 zien er niet zo fraai uit, dat is dan ook de reden waarom het Chebyshev-filter voor faselineaire toepassingen (audio) minder geschikt is. Het stapspanningsgedrag (figuur 3) toont ook weer de nodige uitslingerverschijnselen, vergelijkbaar met de responsies van het 0,1-dB-filter van vorige maand.

Tabel 2. Genormaliseerde komponentenwaarden voor passief laagdoorlaatfilter met een verhouding tussen in en uitgangsimpedantie van 2:1 voor even-ordefilters en 1:1 voor onevenorde-filters.

Orde n	C1	L1	C2	L2	C3	L3	C4	L4	C5	L5
2	0,1564	0,3347
3	0,2966	0,2038	0,2966
4	0,1345	0,4329	0,1971	0,3159
5	0,2876	0,2073	0,4283	0,2073	0,2876
6	0,1321	0,4304	0,2055	0,4571	0,1969	0,3113
7	0,2848	0,2063	0,4325	0,2204	0,4325	0,2063	0,2848
8	0,1313	0,4284	0,2056	0,4637	0,2094	0,4584	0,1963	0,3095
9	0,02589	0,2056	0,4323	0,2216	0,4414	0,2216	0,4323	0,2056	0,02589
10	0,1309	0,4273	0,2053	0,4642	0,2108	0,4678	0,2099	0,4581	0,1959	0,3087
	L1	C1	L2	C2	L3	C3	L4	C4	L5	C5

Tabel 3. Genormaliseerde komponentenwaarden voor passief laagdoorlaatfilter met bron-impedantie van nul ohm.

Orde n	L1	C1	L2	C2	L3	C3	L4	C4	L5	C5
2	0,208	0,1551
3	0,2502	0,2416	0,1483
4	0,2286	0,3006	0,2421	0,1453
5	0,2594	0,2769	0,3058	0,2409	0,1438
6	0,2327	0,3151	0,2833	0,3064	0,24	0,1429
7	0,262	0,2829	0,3232	0,2848	0,3062	0,2393	0,1424
8	0,2341	0,3187	0,2904	0,3253	0,2851	0,3059	0,2388	0,1421
9	0,2631	0,2847	0,3274	0,2926	0,326	0,285	0,3056	0,2384	0,1418
10	0,2348	0,32	0,2926	0,33	0,2934	0,3262	0,285	0,3053	0,2382	0,1416

Tabel 4. Genormaliseerde komponentenwaarden voor aktieve filters met enkelvoudige tegenkoppeling.

Orde n	C1	C2	C1	C2	C3
2	0,3104	0,104
3			1,7873	0,3581	0,01424
4	0,992	0,02868
	0,4109	0,2069
5	0,5059	0,01821
			1,0889	0,5279	0,04827
6	2,1327	0,01258
	0,781	0,05957
	0,5717	0,3057
7	2,8759	0,0092
	1,0259	0,03866
			1,2689	0,7135	0,0748
8	3,7322	0,007017
	1,311	0,02728
	0,8757	0,0844
	0,7425	0,4054
9	4,7014	0,005531
	1,6329	0,02036
	1,0659	0,05442
			1,522	0,904	0,09963
10	5,7869	0,004472
	1,9942	0,01584
	1,2809	0,03829
	1,0159	0,1078
	0,9167	0,5053

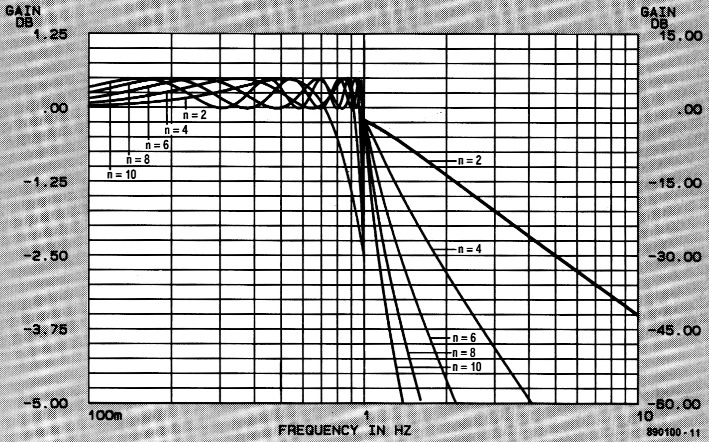
Figuur 1. De frekwentiekarakteristieken voor 0, 5-dB-Chebyshev-filters.

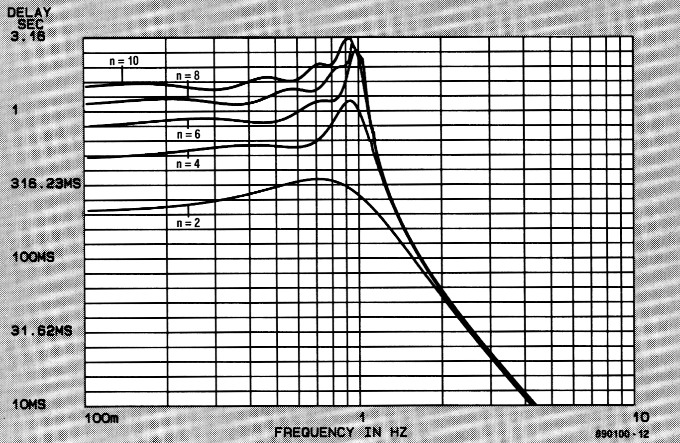
Figuur 2. De bijbehorende tijd vertragingskurves.

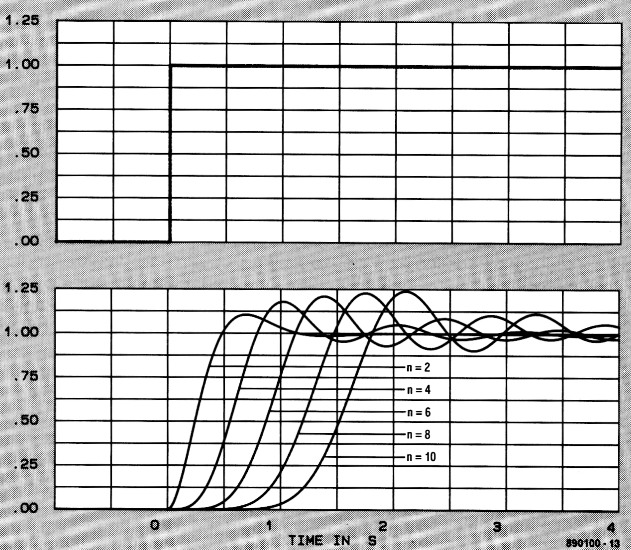
Figuur 3. Stapspanningresponsie voor dit type filter.

Voorbeelden

Ditmaal slechts een voorbeeld waarbij echter twee mogelijke oplossingen worden gegeven.

Ontwerp een aktief banddoorlaatfilter met een doorlaatgebied van 11500 tot 12500 Hz (-3 dB). De verwakking moet bij 8 en 18 kHz minstens 40 dB bedragen. We proberen de aktieve schakeling zo eenvoudig mogelijk te houden. Aangezien er geen eisen gesteld worden aan de toegestane rimpel in de doorlaatband, kiezen we voor een 0,5-dB-Chebyshev-filter omdat dit van alle toe nu toe behandelde filters de steilste hellingen heeft. Eerst berekenen we aan de hand van de -3-dB-punten de centrale frekwentie:

f_c = √(f_l × f_h) = 11990 Hz

Daarna moeten de "komplementaire" frekwenties gezocht worden bij de frekwenties van 8 en 18 kHz, om de steilste kombinatie te vinden. Bij 8 kHz hoort een frekwentie van:

f2 = 11990² / 8000 = 17970 Hz

Bij 18 kHz hoort een frekwentie van:

f1 = 11990² / 18000 = 7987 Hz

De steilste kombinatie is dus 8000 / 17970 Hz, hoewel de verschillen zo klein zijn dat we beide kombinaties zouden kunnen gebruiken. De bandbreedte bij -40 dB bedraagt dus: 17970 - 8000 = 9970 Hz In de karakteristieken moeten we gaan kijken hoe dat met zo weinig mogelijk filtersekties bereikt kan worden. Hiervoor moeten we de verhouding nemen tussen de zojuist berekende bandbreedte bij -40 dB en de -3-dB-bandbreedte: 9970 / 1000 = 9,97.

Naar schatting zal de demping van een tweedeorde-filter volgens figuur 1 daar zo'n 42 dB bedragen. Ruim voldoende om aan de gestelde eisen te voldoen!

Als filter-opzet wordt in eerste instantie een bandfilter met meervoudige tegenkoppeling gekozen (zie figuur 5, deel 5), waarvan twee sekties achter elkaar moeten worden geschakeld voor het verkrijgen van een tweede-orde-filter. Voor de berekening van de komponentenwaarden moeten eerst de polen voor een tweede-orde-filter in figuur 1 worden opgezocht:

-α = 0,502
±β = 0,7278

De Q-faktor van het filter moet zijn:

Q = 11990 / 100O = 11,99

Dan volgen de noodzakelijke berekeningen (zie voor de formules deel 5):

C = 0,7817
Qs = 23,89
D = 1,022
f_sa = 11731 Hz
f_sb = 12254 Hz

De versterking Vs is:

V_sa = 1,444
V_sb = 1,444

Dan kunnen de komponentenwaarden worden berekend. Voor de kondensatorwaarde wordt 4,7 nF genomen.

Eerste sektie:
R3 = 137,9 kΩ
Rl = 47,76 kΩ
R2 = 60,48 Ω

Tweede sektie:
R3 = 132 kΩ
R1 = 45,72 kΩ
R2 = 57,89 Ω

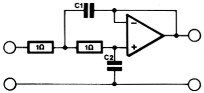
In de praktijk zal deze schakeling (zie figuur 4) wel funktioneren, maar de Q van elke sektie is vrij hoog. Bovendien is de spanningsverzwakking aan de ingangen zo sterk dat dit gegarandeerd ruisproblemen zal veroorzaken.

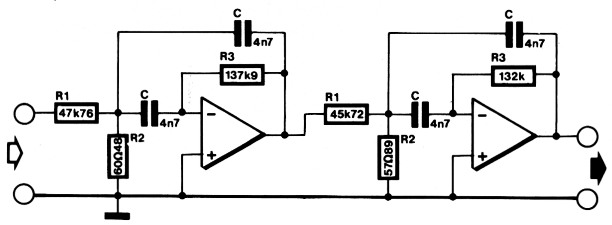
Figuur 4. Een tweede-orde aktief bandfilter met slechts een opamp per sektie. Bij hogere Q's, zoals in het berekende voorbeeld, ontstaan snel problemen.

Men zal verder zeer goede opamps moeten kiezen om de gewenste resultaten te bereiken bij zo'n hoge frekwenties. Daarom berekenen we hetzelfde filter nog eens met een dubbeleopamp-filter (zie figuur 6, deel 5). Dit type kan beter uit de voeten met hogere Q's. De sektieberekeningen blijven ongewijzigd, alleen de komponentenwaarden moeten opnieuw berekend worden.

Eerste sektie:
R3 = R4 = 2,887 kΩ
R1 = 95,51 kΩ
R2 = 248,1 kΩ

Tweede sektie:
R3 = R4 = 2,763 kΩ
R1= 91,44 kΩ
R2 = 237,5 kΩ

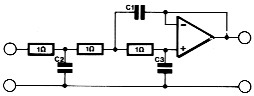
In figuur 5 is het schema van de komplete schakeling volgens deze opzet gegeven. Niet alleen hebben de opamps het hier een stuk makkelijker, maar ook de verzwakking aan de ingangen is bijna geheel verdwenen. In beide gevallen zullen de toleranties van de gebruikte komponenten gering moeten zijn (minstens 1%-komponenten), anders zullen de kurves niet overeen komen met de berekende.

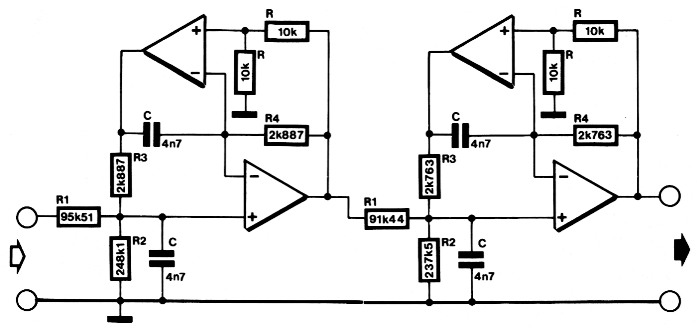
Figuur 5. Hetzelfde filter als in figuur 4, maar nu uitgevoerd met een dubbeleopamp-konfiguratie.

Tot zo ver deel 9. Na de halfgeleidergids nemen we de filter-draad weer op.

Deel 1 - Deel 2 - Deel 3 - Deel 4 - Deel 5 - Deel 6 - Deel 7 - Deel 8 - Deel 9 - Deel 10