Praktische filtertechniek 8; Chebyshev-filters 1
Een van de steilste filtertypen is het Chebyshevfilter. Naast het voordeel van de steile filterhelling staat echter een nadeel dat de toepassing nogal beperkt: een rimpel in de doorlaatband. Het Chebyshev-filter kan op verschillende manieren gedimensioneerd worden, waarbij de rimpel steeds beperkt blijft tot een bepaalde waarde. In dit deel vindt u de tabellen voor Chebyshev-filters met een rimpel van 0,1 dB.
De Chebyshev-funktie is een van de meest optimale funkties om een filter te realiseren, waarbij een scherpe knik rond het kan-telpunt wordt gekombineerd met een zeer steile helling. Daarbij ontstaat echter wel een "slinger" in de doorlaatband, die afhankelijk van de dimensionering binnen een bepaalde waarde blijft. In het algemeen kunnen we stellen dat de helling iets steiler wordt als voor de rimpel in de doorlaatband een grotere waarde wordt toegestaan. In de praktijk is dat echter al snel aan grenzen gebonden, want een filter met een doorlaat-rimpel van 1 dB zal vaak niet meer bruikbaar zijn. Om die reden beperken we ons hier tot twee Chebyshev-varianten. In dit deel worden de tabellen en kurves gegeven voor Chebyshev-filters met een rimpel van 0,1 dB en in deel 9 volgen dan de gegevens voor filters met een rimpel van 0,5 dB. Dat zijn waarden die in de praktijk goede diensten kunnen bewijzen.
Een algemeen nadeel van Chebyshev-filters is de zeer onregelmatige looptijdkarakteristiek, waarmee men bij sommige toepassingen zeker rekening moet houden. Dat maakt dit type bijv onbruikbaar voor luidspreker-filters.
De berekening van de Chebyshev-polen kan op twee manieren gebeuren. Men kan natuurlijk uitgaan van de Chebyshev-polynomen, maar het is ook mogelijk om de polen van de Butterworth-overdrachtsfunktie te verplaatsen door het reële deel van de polen met een konstante faktor te vermenigvuldigen, waardoor deze op een ellips terechtkomen in plaats van een cirkel. Bij de Chebyshev-polynomen moet nog worden opgemerkt dat het kaneelpunt niet overeen komt met het -3-dB-punt. In de tabellen is daar echter rekening mee gehouden en is alles teruggerekend naar een gewoon -3-dB-kantelpunt.
| Orde n | Reële deel -α | Imaginaire deel ±β |
|---|---|---|
| 2 | 0,6074 | 0,7112 |
| 3 | 0,348 | 0,871 |
| 0,696 | ||
| 4 | 0,2174 | 0,9292 |
| 0,5248 | 0,3849 | |
| 5 | 0,1466 | 0,9565 |
| 0,3838 | 0,5912 | |
| 0,4744 | ||
| 6 | 0,1049 | 0,9715 |
| 0,2865 | 0,7112 | |
| 0,3913 | 0,2603 | |
| 7 | 0,07846 | 0,9806 |
| 0,2198 | 0,7863 | |
| 0,3177 | 0,4364 | |
| 0,3526 | ||
| 8 | 0,06079 | 0,9864 |
| 0,1731 | 0,8363 | |
| 0,2591 | 0,5588 | |
| 0,3056 | 0,1962 | |
| 9 | 0,04844 | 0,9905 |
| 0,1395 | 0,871 | |
| 0,2137 | 0,6465 | |
| 0,2621 | 0,344 | |
| 0,2789 | ||
| 10 | 0,03947 | 0,9934 |
| 0,1145 | 0,8962 | |
| 0,1784 | 0,7112 | |
| 0,2248 | 0,4566 | |
| 0,2492 | 0,1573 |
Chebyshev met 0,1 dB rimpel
In de tabellen 1...5 zijn alle benodigde gegevens vermeld voor de berekening van een Chebyshevfilter van de tweede tot de tiende orde, met een rimpel van 0,1 dB. Bij tabel 2 moet u even goed opletten, want daar is iets bijzonders aan de hand. Bij een even-orde-filter is het niet mogelijk om een Chebyshev-filter te berekenen voor een gelijke in- en uitgangsimpedantie. Daarom gelden de waarden voor de even-orde-filters in tabel 2 voor een verhouding tussen in- en uitgangsweerstand van 2:1 (voor een π-filter) of 1:2 (voor een T-filter).
 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Orde n | C1 | L1 | C2 | L2 | C3 | L3 | C4 | L4 | C5 | L5 |
| 2 | 0,08908 | 0,486 | ||||||||
| 3 | 0,228 | 0,2536 | 0,288 | |||||||
| 4 | 0,06999 | 0,5136 | 0,1539 | 0,4546 | ||||||
| 5 | 0,2071 | 0,2476 | 0,3567 | 0,2476 | 0,2071 | |||||
| 6 | 0,06584 | 0,4883 | 0,1524 | 0,5908 | 0,1559 | 0,4446 | ||||
| 7 | 0,2008 | 0,2419 | 0,3564 | 0,2674 | 0,3564 | 0,2419 | 0,2008 | |||
| 6 | 0,06433 | 0,4779 | 0,1498 | 0,5876 | 0,161 | 0,5987 | 0,1554 | 0,4407 | ||
| 9 | 0,1981 | 0,239 | 0,3536 | 0,2678 | 0,3654 | O,2678 | 0,3536 | 0,239 | 0,1981 | |
| 10 | 0,06363 | 0,4729 | 0,1484 | 0,5833 | 0,1606 | 0,6036 | 0,1626 | 0,5995 | 0,155 | 0,4388 |
| L1 | C1 | L2 | C2 | L3 | C3 | L4 | C4 | L5 | C5 | |
 | ||||||||||
 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Orde n | L1 | C1 | L2 | C2 | L3 | C3 | L4 | C4 | L5 | C5 |
| 2 | 0,2214 | 0,1304 | ||||||||
| 3 | 0,2408 | 0,2402 | 0,114 | |||||||
| 4 | 0,2404 | 0,2814 | 0,2316 | 0,107 | ||||||
| 5 | 0,2485 | 0,2876 | 0,2811 | 0,2256 | 0,1036 | |||||
| 6 | 0,2441 | 0,2998 | 0,2913 | 0,2783 | 0,2218 | 0,1016 | ||||
| 7 | 0,2506 | 0,2957 | 0,3057 | 0,2908 | 0,276 | 0,2914 | 0,1004 | |||
| 8 | 0,2454 | 0,3041 | 0,3025 | 0,3064 | 0,2897 | 0,2742 | 0,2178 | 0,0996 | ||
| 9 | 0,2515 | 0,298 | 0,3117 | 0,3039 | 0,306 | 0,2886 | 0,273 | 0,2166 | 0,09904 | |
| 10 | 0,2461 | 0,3056 | 0,3058 | 0,3135 | 0,304 | 0,3055 | 0,2878 | 0,272 | 0,2158 | 0,09864 |
 |  |
||||
|---|---|---|---|---|---|
| Orde n | C1 | C2 | C1 | C2 | C3 |
| 2 | 0,2607 | 0,1107 | |||
| 3 | 1,0589 | 0,2905 | 0,02141 | ||
| 4 | 0,7308 | 0,03836 | |||
| 0,3024 | 0,1975 | ||||
| 5 | 1,0838 | 0,02515 | |||
| 0,7076 | 0,4011 | 0,06054 | |||
| 6 | 1,5169 | 0,01767 | |||
| 0,555 | 0,07826 | ||||
| 0,4063 | 0,2827 | ||||
| 7 | 2,026 | 0,01304 | |||
| 0,7235 | 0,05301 | ||||
| 0,8236 | 0,5287 | 0,09061 | |||
| 8 | 2,6165 | 0,01001 | |||
| 0,9188 | 0,03817 | ||||
| 0,6139 | 0,1097 | ||||
| 0,3613 | 0,3697 | ||||
| 9 | 3,285 | 0,00793 | |||
| 1,1411 | 0,02884 | ||||
| 0,7445 | 0,07409 | ||||
| 0,9858 | 0,6622 | 0,1191 | |||
| 10 | 4,0298 | 0,00643 | |||
| 1,3889 | 0,02258 | ||||
| 0,8917 | 0,0534 | ||||
| 0,7078 | 0,1394 | ||||
| 0,6384 | 0,4579 | ||||
In de filterkarakteristieken is het steile verloop te zien van dit type filter, terwijl van de rimpel nauwelijks iets te zien is (figuur 1). De looptijdkarakteristieken (figuur 2) laten een iets minder goed beeld zien, zeker vergeleken met de vorige filtertypen. De stapresponsie (figuur 3) heeft nogal wat last van uitslingerverschijnselen. Opvallend is overigens dat looptijd-gedrag en stapresponsie niet veel beter worden als de rimpel kleiner wordt gekozen.
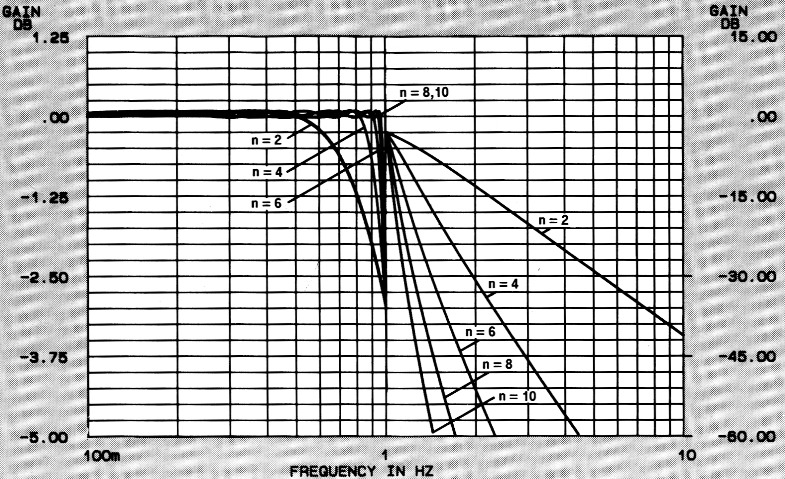
Figuur 1. De frekwentiekarakteristieken voor Chebyshev-filters met 0,1 dB rimpel.
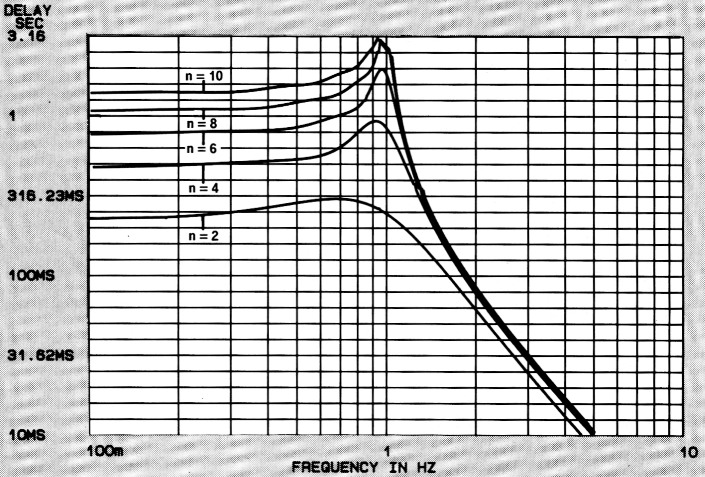
Figuur 2. De bijbehorende tijdvertragingskurves.
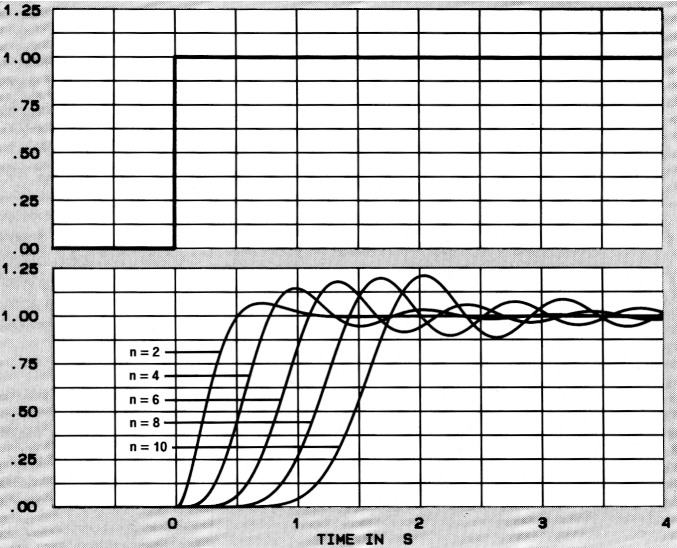
Figuur 3. De responsie op een stapspanning.
Voorbeelden
Ook nu weer twee berekeningsvoorbeelden, waarbij we eens gaan kijken naar een bandfilter en een wat komplexer laagdoorlaatfilter met een state-variablefilter.
Voorbeeld 1
Bereken een passief bandfilter met een centrale frekwentie van 1 kHz en een bandbreedte van 100 Hz. Bij 900 en 1100 Hz moet de verzwakking minstens 20 dB bedragen. Het filter wordt aangesloten op een versterker met een uitgangsimpedantie van praktisch nul ohm en afgesloten met een belasting van 600 Ω.Aangezien de centrale frekwentie al is opgegeven, hoeven we die niet uit de -3-dB-punten te berekenen. We berekenen de bij 900 en 1100 Hz behorende frekwenties aan de tegenoverliggende kant van het bandfilter, om zo de steilste kombinatie te vinden. Bij 900 Hz hoort: F2 = 10002 / 900 = 1111 Hz Bij 1100 Hz hoort: f1 = 10002 / 1100 = 909 Hz Het dichtst bij 1 kHz ligt de kombinatie 909 / 1100 Hz. De bandbreedte op de -20-dB-punten bedraagt dus:
1100 - 909 = 191 Hz.
We moeten nu in de karakteristieken een filter gaan zoeken dat bij een genormaliseerde frekwentie van 191 / 100 = 1,91 Hz een verzwakking van minstens 20 dB geeft (denk er aan dat de bandbreedte van het bandfilter als uitgangspunt wordt genomen voor de dimensionering van het laagdoorlaatfilter, dus niet de centrale frekwentie). Aangezien we juist met de Chebyshevfilters bezig zijn, kiezen we hier een derde-orde 0,1dB-Chebyshev-filter. Dat geeft bij f = 2 Hz een verzwakking van circa 22 dB (geschat tussen tweede-en vierde-orde filter).
In figuur 4a is de laagdoorlaat-opzet getekend van een derde-orde filter. De genormaliseerde komponentenwaarden volgen uit tabel 3. Daarna worden de "echte" waarden berekend voor een afsluitimpedantie van 600 Ω en een kaneelpunt dat gelijk is aan de -3-dBbandbreedte (100 Hz):
L1 = L × R / f = 1,4448 H
C1 = C / (R × f)= 4,003 ×10-6 = 4 µF
L2 = L × R / f = O,684 H

Figuur 4. De dimensionering van een passief bandfilter.
a: genormaliseerd hoogdoorlaatfilter, b: dimensionering voor de gewenste bandbreedte, c: omzetting naar bandfilter.
Vervolgens volgt een laagdoorlaat- naar banddoorlaat-transformatie (zie deel 5), zodat het filter uit figuur 4c ontstaat. De resterende komponenten worden tot slot berekend met de formules die in figuur 3 van deel 5 gegeven zijn:
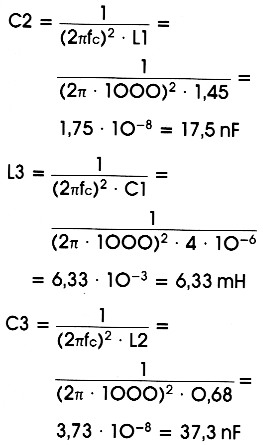
U ziet dat de centrale f rekwentie van het bandfilter pas in de berekeningen komt kijken bij de dimensionering van de komponenten die tijdens de transformatie zijn toegevoegd.
Voorbeeld 2
Ontwerp een aktief laagdoorlaat-filter met een kantelpunt op 3 kHz en een steilheid van 12 dB per oktaaf. Het kan-telpunt moet nauwkeurig ingesteld kunnen worden. De versterking van het filter moet vijf maal bedragen. Om dit te verwezenlijken kiezen we een statevariable-filter (zie deel 3, figuur 5). Ook hier nemen we voor het gemak een 0,1-dB-Chebyshev-filter, aangezien de benodigde tabellen in dit deel staan. Voor een state-variablefilter gaan we uit van de polen voor een tweede-orde filter uit tabel 1:
-α = 0,6074
β=±0,7112
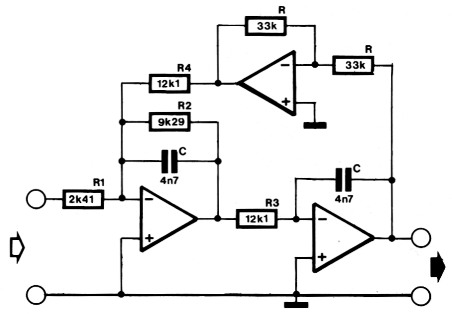
Figuur 5. Een voorbeeld van een state-variable-filter met een kantelfrekwentie van 3 kHz.
Eerst wordt een waarde voor C gekozen, laten we zeggen 4,7 nF. Voor de weerstanden R wordt een waarde van 33 kΩ genomen. Nu kunnen direkt de overige weerstandswaarden berekend worden. We gebruiken daarvoor de formules die in deel 3 hiervoor zijn gegeven, waarbij we er aan moeten denken dat alle waarden nog eens door de kanteifrekwentie moeten worden gedeeld (de formules gelden voor f = 1 Hz):

Voor R2 en R4 kan een kombinatie van een weerstand en een instelpotmeter worden genomen, zodat het kantelpunt en de Q-faktor van het filter nauwkeurig kunnen worden ingesteld.
Tot slot willen we nog even wijzen op twee foutjes die in het stukje over het statevariable-filter in deel 3 zijn geslopen. Wie het voorgaande voorbeeld nauwkeurig heeft gevolgd, zal al gemerkt hebben dat de weerstanden R2 en R4 voor het afregelen moeten worden gebruikt en niet R1 en R3, zoals in deel 3 werd vermeld. R4 dient voor het afregelen van de maximale uitgangsspanning bij fo op de uitgang van A1 en met R2 wordt de bij de berekende Q-faktor behorende bandbreedte ingesteld.
Volgende keer: 0,5-dB-Chebyshev-filters.
Deel 1 - Deel 2 - Deel 3 - Deel 4 - Deel 5 - Deel 6 - Deel 7 - Deel 8 - Deel 9 - Deel 10