Praktische filtertechniek 7; Bessel-filters

Nadat we vorige maand de karakteristieken en tabellen voor de Butterworth-filters bekeken hebben, is het nu de beurt aan een filtertype dat wat minder steile hellingen heeft, maar daarvoor in de plaats wel een uitstekend impuisgedrag en zeer vlakke looptijdkarakteristieken biedt: het Bessel-fiiter.

Zoals we al gezien hadden, biedt het Butterworth-filter een kombinatie van zowel redelijk steile hellingen als een redelijk goed impuls-gedrag. Afhankelijk van het toepassingsgebied zal men niet altijd een dergelijk kompromis willen, maar is voornamelijk een eigenschap belangrijk. Bij de Bessel-funktie staat het lineaire-fasegedrag voorop, zoals we ook duidelijk kunnen zien in figuur 2. Dit type filter geeft de meest lineaire tijdvertraging van alle filtersoorten. Eigenlijk is dat helemaal niet zo gek, want de Bessel-amplitudekarakteristiek geeft gewoon een rechte dalende lijn te zien als we deze op een lineaire schaal uitzetten. Alleen door het gewoonlijk gebruikte logaritmische verloop ontstaat een kurve die eruit ziet als een gewone filterhelling. De overdrachtskarakteristiek van het Bessel-filter is dus vrij slap. Een afval van n × 6 dB wordt niet gehaald (n = orde van filter) en vooral rond het kantelpunt is de "bocht" erg flauw. Hierop heeft de orde van het filter nauwelijks invloed.

Tabel 1. Bessel-poolpunten.
Orde n	Reële deel -α	Imaginaire deel ±β
2	1.103	0,6368
3	1,0509	1,0025
3	1,327
4	0,9877	1,2476
4	1,3596	0,4071
5	0,9606	1,4756
	1,3851	0,7201
	1,5069
6	0,9318	1,664
	1,3836	0,9727
	1,5735	0,3213
7	0,9104	1,8375
	1,3797	1,1923
	1,613	0,5896
	1,6853
8	0,8955	2,0044
	1,3787	1,3926
	1,6419	0,8253
	1,7627	0,2737
9	0,8788	2,1509
	1,3683	1,5685
	1,6532	1,0319
	1,8081	0,5126
	1,8575
10	0,8688	2,3002
	1,365	1,7395
	1,6667	1,2248
	1,8477	0,7297
	1,9335	0,2423

De tabellen

De tabellen met de data voor het berekenen van Bessel-filters zijn hetzelfde opgezet als de Butterworth-tabellen, zodat men met het gebruik hiervan weinig problemen zal hebben. Ook hier gelden alle komponenten-waarden voor een filter met een kantelpunt van 1 Hz. Naast de polen voor de Bessel-filters van de tweede tot de tiende orde (tabel 1) vindt u in tabel 2 de komponentenwaarden voor een passief filter met gelijke in- en uitgangsimpedantie, in tabel 3 de komponentenwaarden voor een passief filter met een te verwaarlozen bronimpedantie en in tabel 4 de waarden voor een aktief Bessel-filter.

Tabel 2. Genormaliseerde komponentenwaarden voor passief laagdoorlaatfilter met identieke in- en uitgangsimpedantie.

Orde n	C1	L1	C2	L2	C3	L3	C4	L4	C5	L5
2	0,0916	0,3418
3	0,0537	0,1545	0,3507
4	0,03715	0,107	0,1721	0,3566
5	0,02774	0,08072	0,128	0,1768	0,3594
6	0,02172	0,06369	0,1017	0,1359	0,1771	0,3604
7	0,0176	0,05187	0,08354	0,1117	0,1383	0,1759	0,3606
8	0,01463	0,04327	0,07017	0,09447	0,1162	0,1384	0,1744	0,3606
9	0,01241	0,03681	0,06	0,0813	0,1004	0,1179	0,1375	0,1729	0,3605
10	0,0107	0,0318	0,05204	0,07089	0,08798	0,1033	0,1181	0,1363	0,1716	0,3603
	L1	C1	L2	C2	L3	C3	L4	C4	L5	C5

Tabel 3. Genormaliseerde komponentenwaarden voor passief laagdoorlaatfilter met bronimpedantie van nul ohm.

Orde n	L1	C1	L2	C2	L3	C3	L4	C4	L5	C5
2	0,2167	0,07224
3	0,2329	0,1341	0,04657
4	0,2389	0,1557	0,09751	0,03365
5	0,2407	0,1628	0,1199	0,07526	0,02575
6	0,2407	0,1644	0,1293	0,09664	0,06024	0,02048
7	0,2401	0,1638	0,1328	0,1075	0,08007	0,04954	0,01677
8	0,2394	0,1626	0,1336	0,1127	0,0914	0,06769	0,04163	0,01405
9	0,2388	0,1612	0,1331	0,1149	0,09775	0,07899	0,05816	0,03562	0,012
10	0,2383	0,1599	0,1321	0,1155	0,1011	0,08596	0,06911	0,05064	0,03091	0,01039

Tabel 4. Genormaliseerde komponentenwaarden voor aktieve filters met enkelvoudige tegenkoppeling.

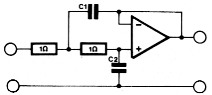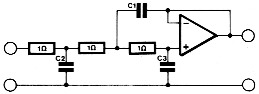Orde n	C1	C2	C1	C2	C3
2	0,1443	0,1082
3			0,2265	0,1572	0,04039
4	0,1611	0,006207
4	0,117	0,1047
5	0,1657	0,04934
5			0,1607	0,1387	0,04926
6	0,1708	0,04076
	0,115	0,07695
	0,1011	0,09708
7	0,1751	0,03444
	0,1154	0,06607
			0,1358	0,124	0,04818
8	0,1776	0,02956
	0,1155	0,05714
	0,09693	0,07737
	0,09029	0,08817
9	0,181	0,02591
	0,1163	0,05025
	0,09626	0,06926
			0,1204	0,1125	0,04538
10	1,1832	0,02287
	0,1166	0,04444
	0,09549	0,06201
	0,08613	0,07452
	0,08231	0,08104

De karakteristieken

De karakteristieken in figuur 1...3 tonen direkt de voor- en nadelen van het Bessel-filter. De demping in het spergebied is bijvoorbeeld veel geringer dan bij het Butterworth-filter. De knik rond het -3-dB-punt, die in het linker gedeelte te zien is, ziet er voor alle ordes identiek uit. In figuur 2 zien we de positieve eigenschappen van het Bessel-filter. De tijdvertragingskurves lopen uiterst lineair tot het kantelpunt (ongeveer vanaf derde orde). Bij hogere ordes blijft de tijdvertraging zelfs nog een stuk na de kantelfrekwentie konstant. Dit lineaire-fasegedrag vinden we ook terug in de stap-responsies van figuur 3. Er is praktisch geen overshoot en er treden ook geen uit-slingerverschijnselen op.

Fig 1
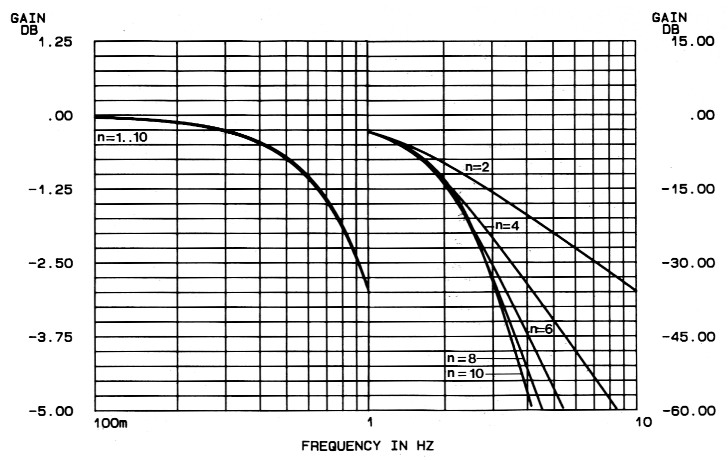
Figuur 1. De frekwentiekarakteristieken voor Bessel-filters.

Fig 2
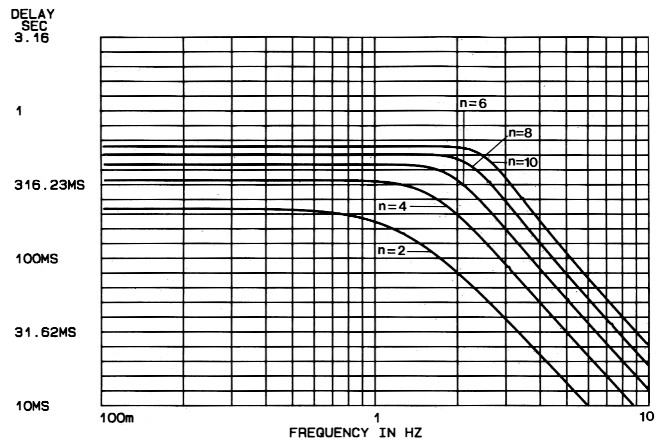
Figuur 2. De bijbehorende vertragingskurves voor de Bessel-filters.

Fig 3
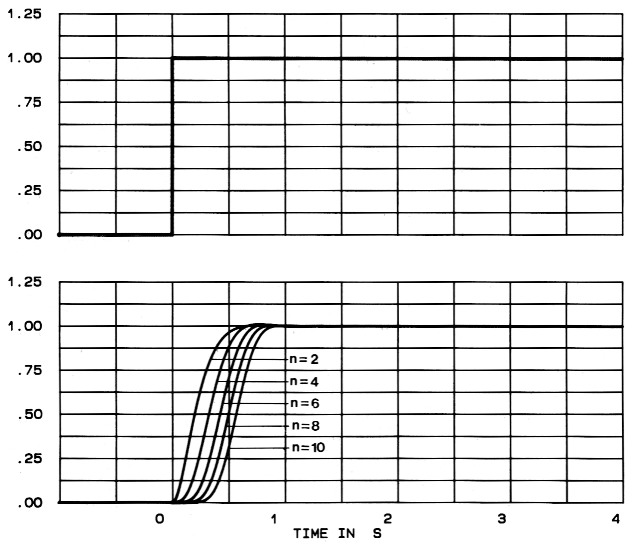
Figuur 3. De responsie op een stapspanning.

Voorbeelden

Voorbeeld 1

Ontwerp een derde-orde laag- en hoogdoorlaatfilter voor een luidsprekersysteem met een nominale impedantie van 8 Ω. Het kantelpunt moet op 2500 Hz liggen en het dient een Bessel-filter te zijn.

Voor een luidsprekerfilter gaan we uit van een passief filter met een te verwaarlozen bron-impedantie. De berekening van het laagdoorlaatfilter is uiterst eenvoudig. We nemen een standaard passief laagdoorlaatfilter en vullen hier de waarden in voor een derde-orde filter uit tabel 3 (figuur 4a). Vervolgens worden die waarden omgerekend naar de werkelijke afsluit-impedantie (8 Ω) en het werkelijke kaneelpunt (2500 Hz):

C' = C / (f × R)
L' = L × R / f

Fig 4
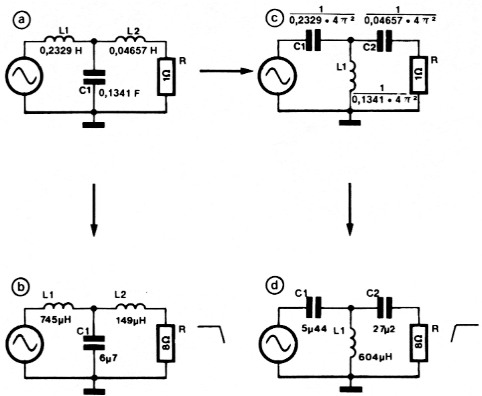
Figuur 4. De dimensionering van een passief laag-en hoogdoorlaatfilter. R_L = 8 Ω, kantelfrekwentie 2500 Hz.

Het daaruit resulterende filter is afgebeeld in figuur 4b. Daarna moet het hoogdoorlaatfilter worden berekend. Alle kondensatoren in het laagdoorlaatfilter worden daartoe vervangen door spoelen en alle spoelen door kondensatoren. In deel 3 hebben we gezien dat de genormaliseerde filterwaarden voor een hoogdoorlaatfilter kunnen worden gevonden door de genormaliseerde laagdoorlaatwaarden "om tekeren". In figuur 4c is dat gedaan, alleen is overal nog een faktor 4π² toegevoegd. Dat is nodig omdat de formules 1/C en 1/L gelden voor genormaliseerde waarden bij ω = 1 rad/s. In onze tabellen worden de standaardwaarden echter gegeven voor f = 1 Hz, zodat een korrektiefaktor moet worden toegevoegd bij het omrekenen naar een hoogdoorlaatfilter. De formules zijn dan als volgt, als men de tabellen uit deze artikelen-reeks gebruikt:

C_h = 1 / (4π² × L_l)
L_h = 1 / (4π² × C_l)

Aangezien men toch een rekenmachine nodig heeft om de komponentenwaarden te berekenen, kan die extra faktor gemakkelijk worden meegenomen (evt. voor 4π² × 39,48 invullen). De berekening voor het resulterende hoogdoorlaatfilter voor een afsluit-impedantie van 8 Ω en een kantelfrekwentie van 2500 Hz kan hierna op de vertrouwde manier geschieden (figuur 4d).

Voorbeeld 2

Ontwerp een aktief laagdoorlaatfilter met een kan-telpunt op 20 kHz, waarbij de tijdvertraging konstant blijft tot minimaal 30 kHz. De verzwakking dient bij 100 kHz minstens 50 dB te bedragen.

Voor het interpreteren van de waarden in de karakteristieken moeten de frekwenties eerst worden teruggerekend naar een genormaliseerde frekwentie van 1 Hz. 30 kHz wordt dan 30 / 20 = 1,5 en 100 kHz wordt dan 100 / 20 = 5. Nu kunnen we in de karakteristieken gaan kijken welk filter en welke orde aan de gestelde eisen voldoet.

Aangezien een konstante tijdvertraging tot voorbij het kantelpunt wordt gewenst, komt alleen een Bessel-filter in aanmerking. Uit figuur 2 blijkt dat we ongeveer een zesde-ordefilter nodig hebben om de tijdvertraging tot circa 1,5 maal de kantelfrekwentie konstant te houden. Nader onderzoek in figuur 1 geeft aan dat die zesde orde ook nodig is om een verzwakking van minstens 50 dB bij 5 × f_k te halen.

Een zesde-orde-filter is een even-orde-filter, dus moet het filter worden opgebouwd met uitsluitend tweede-orde-sekties (tabel 4). Drie sekties zijn nodig, de kondensatorwaarden kunnen rechtstreeks uit tabel 4 worden overgenomen. Kies daarna een geschikte waarde voor de weerstanden. Met behulp van de formules uit het begin van het eerste voorbeeld worden vervolgens de werkelijke kondensatorwaarden voor de gebruikte weerstanden en het gewenste kantelpunt berekend (figuur 5b). We geven weer twee berekeningsvoorbeelden voor de eerste sektie:

C1 = 0,1708 / (20.000 × 2200) = 3,88 × 10^-9 = 3,88 nF
C2 = 0,04076 / (20.000 × 2200) = 926 × 10^-12 = 926 pF

Fig 5
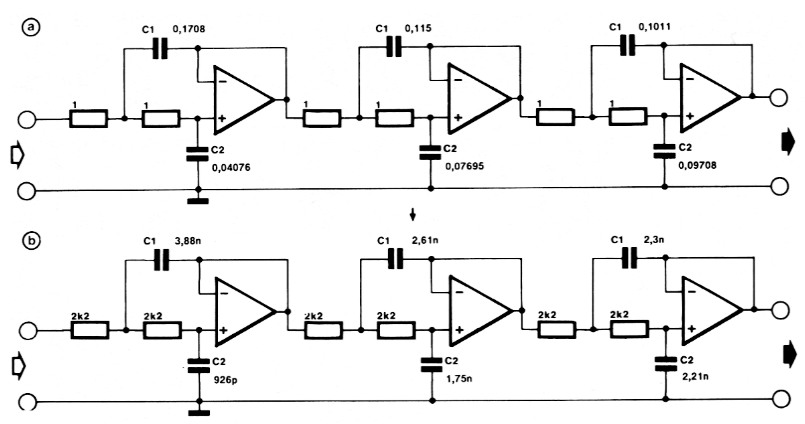
Figuur 5. Een aktief Bessel-filter van de zesde orde, kantelpunt 20 kHz.

Volgende maand gaan we verder met de Chebyshevfilters.